FDEM的材料参数输入
文章摘要
联合的有限元-离散元方法(FDEM)是一种能够模拟多个相互作用物体动态行为的数值方法,由Munjiza等人于1995年提出。FDEM允许自动处理离散块体,无需预先划分,能够模拟物体的弹性变形、平移、旋转和断裂,产生新的离散体。该方法结合了有限元法(FEM)评估变形和断裂破坏准则,以及离散元法(DEM)处理新的接触和离散体的相互作用。
文章讨论了FDEM中材料参数的输入,包括变形参数(如密度、阻尼因子、本构模型、弹性模量和泊松比)、强度参数(如摩擦系数、粘结力、抗拉强度和断裂能)以及罚参数(法向接触罚、切向接触罚和断裂罚)。这些参数对于模拟岩石断裂和不连续体的行为至关重要。文章还提供了参数推荐值和设置建议,以确保数值模拟的准确性和稳定性。
参考文献部分列出了多篇关于FDEM在岩石滑坡、脆性页岩断裂行为、岩石破裂和地震性、以及深部隧道开挖中应用的研究论文,展示了FDEM方法在岩土工程模拟中的广泛应用和重要性。
正文
1. 引言
联合的有限元-离散元方法(FDEM)最初由Munjiza等人(1995)提出,这种数值方法允许对多个相互作用的物体进行动态模拟,FDEM离散的块体不需要预先划分,而是使用断裂力学的判别准则进行自动处理。模拟可以从单一的完整域或离散完整体的集 合开始,随着模拟的进行,这些体可以产生弹性变形、平移、旋转、相互作用,并在满足某些断裂准则后发生断裂,从而产生出新的离散体。然后,新产生的体可以进行进一步运动、相互作用、变形和断裂。该方法联合采用了有限元法(FEM)技术评估变形和评价断裂的破坏准则,以及采用了离散元法(DEM)的概念来检测新的接触和处理离散体的平移、旋转和相互作用【岩石断裂的cohesive-zone模拟】。

本文讨论了FDEM材料参数的输入,包括变形参数、强度参数和罚参数。
2. 材料参数
变形参数(Elastic Properties)包括:(2) 阻尼因子 (Damping Factor)对于准静态问题,建议使用临界阻尼系数1来消解不必要的动态振荡。对于动态问题如地震波传播,阻尼系数(viscous damping factor)与岩石的地震质量系数(quality factor)Q有关,如下图所示。

(4) 弹性模量
(5) 泊松比
强度参数(Strength Properties)包括:(1) 摩擦系数(Friction Coefficient)(2) 粘结力(Cohesion), 通常可取其单轴抗压强度UCS的1/4,更精确的值可以使用Hoek-Brown准则估算;(3) 抗拉强度(Tensile Strength), 通常可取其单轴抗压强度UCS的1/10,更精确的值可以使用Hoek-Brown准则估算;(4) Mode I 断裂能 (Mode I Fracture Energy),
首先计算断裂韧度K_ic:
K_ic=0.271+0.107*f_t
其中f_t是岩石的抗拉强度(MPa)
断裂能量=(K_ic)^2/E, 其中E是岩石的弹性模量。
(5) Model II 断裂能 (Mode II Fracture Energy), Model II 断裂能量(Mode II fracture energy): Model I 断裂能量的值乘以10。

有三种罚参数:法向接触罚(normal contact penalty)、切向接触罚(tangential contact penalty)和断裂罚(fracture penalty),切向接触罚p_t与不连续体的切向刚度Kt相吻合(以Pa/m表示),法向接触罚p_n与不连续体的法向刚度Kn(以Pa*m表示)有如下关系:
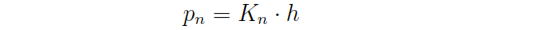
其中h是沿着不连续的有限元长度
一旦材料被分配到有限元网格,就会为每种材料计算推荐的罚系数值。断裂罚和法向接触罚系数的默认值等于杨氏模量值的(10~100)倍。切向罚系数控制着摩擦的运动过程:如果太小,可能会发生材料摩擦力运动的延迟,如果太大则可能导致瞬间摩擦力运动的数值不稳定。对于毫米级的模型,建议使用等于杨氏模量值的(10~100)倍。对于米级的模型,推荐值可表示为下图所示的有限元单元尺寸的函数。此外,为了避免数值不稳定,最小值和最大值应分别等于杨氏模量值得0.01倍和10,000倍。

3. 参考
[1] (2012) Combined finite-discrete element modelling of key instabilities which characterise deep-seated landslides from massive rock slope failure.[2] (2013) Investigating the influence of mechanical anisotropy on the fracturing behaviour of brittle clay shales. [3] (2017) Investigating brittle rock failure and associated seismicity using laboratory experiments and numerical simulations.[4] (2018) Acceleration of a 2D3D finite-discrete element code for geomechanical simulations using General Purpose GPU computing.[5] (2018) The Effect of Jointing in Massive Highly Interlocked Rockmasses Under High Stresses by Using a FDEM Approach.[6] (2018) The Numerical Simulation of Hard Rocks for Tunnelling Purposes at Great Depths - A Comparison between the Hybrid FDEM Method and Continuous Techniques.[7] (2019) Assessing fracturing mechanisms and evolution of excavation damaged zone of tunnels in interlocked rock masses.[8] (2019) Assessment of strain bursting in deep tunnelling by using the finite-discrete element method.[9] (2019) Failure Characterization In Rock Engineering Using A Unified DFN-FDEM Analysis Approach.[10] (2022) Use of continuum and pseudo-discontinuum FEM models in stepwise verification of the FDEM for simulating damage around tunnels in brittle rock.[11] (2024) Application of a Finite-Discrete Element Method Code forModelling Rock Spalling in Tunnels: The Case of the Lyon-Turin Base Tunnel.