有限元|含铰接点的刚架怎么处理?
本文摘要(由AI生成):
本文探讨了平面刚架中铰接点的有限元分析模型处理方法。首先指出,铰接点无法传递弯矩,因此需对含铰接点的单元刚度矩阵进行特殊处理。对于节点2为铰接点的情况,刚度矩阵中K26、K56、K66的值应为0;而节点1为铰接点时,K32、K33、K53的值应为0。通过正确设置这些值,可以建立准确的有限元分析模型,从而有效分析平面刚架在铰接点存在时的力学行为。
如图1所示,平面刚架有一个铰接点。建立有限元分析模型如图2,此时含铰接点的单元该怎么处理?


我们知道,两端刚结平面梁单元的单元刚度矩阵是
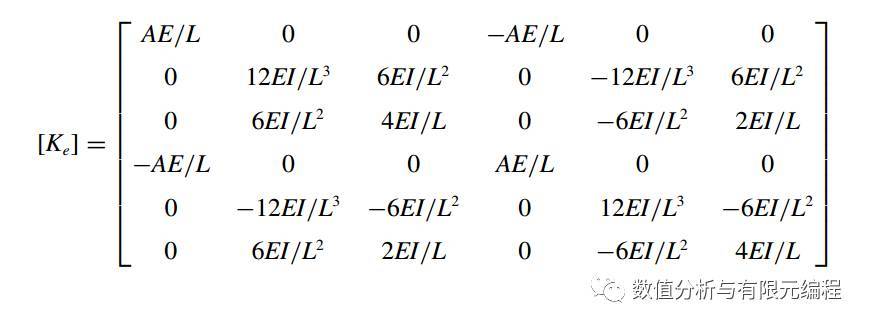
由结构力学可知,有铰的地方不能传递弯矩。再由刚度矩阵的物理意义K26、K36的值是单位力1分别作用在节点1的两个方向时,节点2的弯矩值。
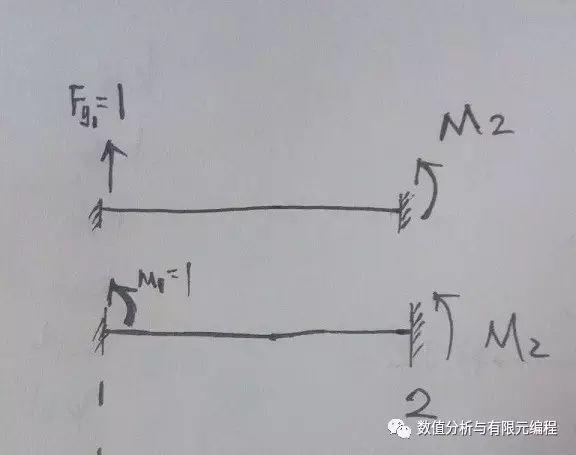
如果单元节点2为铰接点,则K26、K56、K66的值是0,所以节点2为铰接点的单元刚度矩阵是

如果单元节点1为铰接点,则K32、K33、K53的值是0,所以节点1为铰接点的单元刚度矩阵是

登录后免费查看全文
著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2024-04-01
最近编辑:7月前
相关推荐
最新文章
热门文章