平面四节点等参元(Q4)有限元程序算例
本文摘要(由AI生成):
本文研究了平面应力条件下的悬臂梁,材料弹性模量、泊松比、板厚度、长度和高均已知。研究通过自编程序和ANSYS软件,对悬臂梁进行了8个单元的划分,并计算了各节点的位移。结果表明,自编程序和ANSYS软件在计算节点位移上表现相近,验证了自编程序的准确性和可靠性,为悬臂梁结构的分析和优化提供了有力工具。
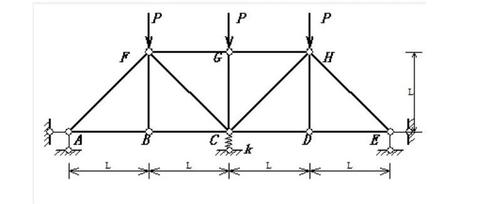
如图所示悬臂梁,假定为平面应力条件。材料弹性模量E=1e6MPa,泊松比v=0.3,板厚度t=10mm,长度l=400mm,高h=100mm。划分8个单元,分别用自编程序和ANSYS计算节点位移。
ANSYS计算结果:
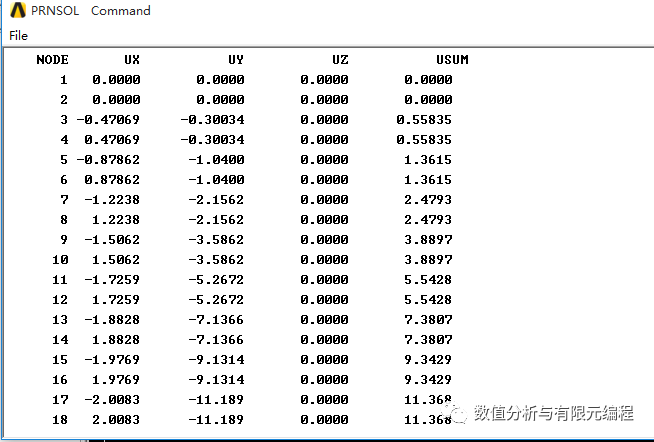

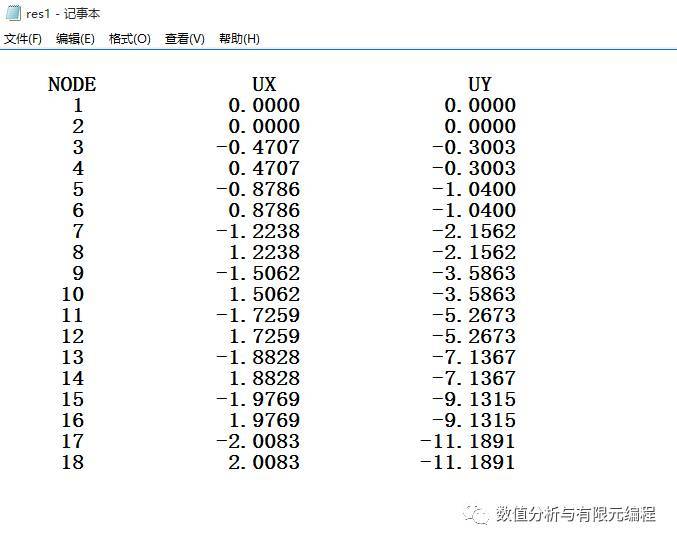
自编程序计算结果:
登录后免费查看全文
著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2024-04-01
最近编辑:7月前
相关推荐
最新文章
热门文章