可视化 | 一个三角形常应变单元后处理例子
本文摘要(由AI生成):
本文介绍了应力云图的概念,它用不同颜色填充等值线来展示应力分布。以悬臂梁为例,通过CST单元建立有限元模型,并利用MATLAB的patch函数进行后处理。patch函数允许创建补片对象,通过指定属性实现插值功能,从而得到梁的变形图。应力云图的Lenged设置可以根据需要调整,本文提供了两种样式。文章旨在展示有限元分析和后处理技术在结构力学中的应用。
昨天提到了应力云图,其实质是用不同的颜色填充等值线。有了结点的应力值,单元内任意一点的应力值是通过插值实现的。下面来看一个悬臂梁的综合后处理。
如图所示,一个悬臂梁受集中力作用。 集中力P=1000N,C=10mm, L=60mm, t=5mm ,弹性模量E=20000MPa,泊松比υ=0.3。

用CST单元建立有限元模型,结点数为21个,单元数为24个,集中力作用在节点2的Y方向。结点19,20,21为约束边界,三个结点的自由度都是固定的。

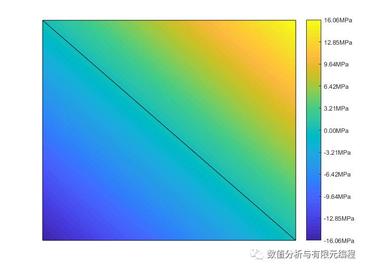
下面是梁的变形图

调用patch(FV)使用结构体FV来创建补片。FV包含如下的结构域:vertices、faces以及facevertexdata(可选)。这些结构域对应补片对象的Vertices、Faces和FaceVerticxCData属性。
调用patch('PropertyName',propertyvalue,...)利用指定的属性/值参数对来指定补片对象的所有属性。除非用户显式的指定FaceColor和EdgeColor的值,否则,MATLAB会使用缺省的属性值。该调用格式允许用户使用Faces和Vertices属性值来定义补片。
调用patch('Facecolor','interp' )就能实现插值功能了。
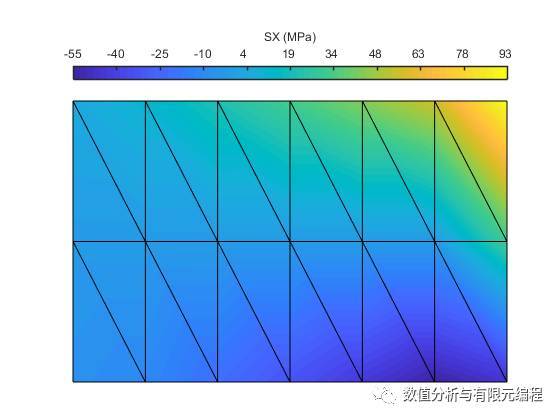
应力云图,Lenged设置成ANSYS风格。

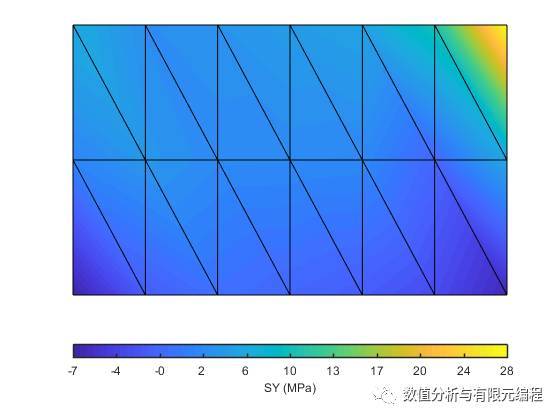

Lenged也可以设置成这样