ANSYS里的对称与反对称约束

本文摘要（由AI生成）：

首先回顾一下结构力学里的概念：在平面内绕对称轴旋转180度，荷载的作用点重合，作用方向相反便是反对称荷载，如果荷载的作用点重合，作用方向相同，便是正对称荷载。通常情况下，当结构受到对称（反对称）荷载作用下，结构内力（应力）分布会有一定的规律，也正是因为有规律，才给我们用部分模型来代替整体模型的可能，一句话来说：我们是用对称性来简化模型和减小计算量的。

以对约束位移自由度的边界条件为例，看看帮助文档给出的信息：

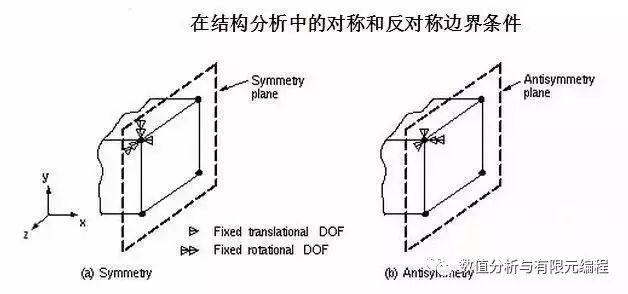
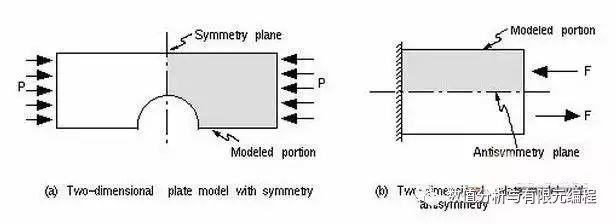
对于3D结构，对称边界指的是对称面外移动和平面内旋转约束为0；反对称边界指的是对称面平面内位移和平面外旋转约束为0，对于2D结构以此类推。具体看下面的表格，一目了然。

施加对称（反对称）约束的APDL命令：

DSYM, Lab, Normal, KCN

Lab：SYMM-正对称，ASYM-反对称；

Normal：X，Y，Z。选定对称面上的节点，然后施加DSYM命令即可。