子空间迭代法求结构自振频率
在结构模态分析中一般不需要求解结构的所有特征对,而只需要求解部分低阶特征对。子空间迭代算法就是用于求解结构部分低阶特征对。许多著名的商业有限元分析软件都有这种求解算法。
子空间迭代法的大致思路是:
一、选取q个线性无关的初始迭代向量组(q>p,p是待求特征对数目)。
二、利用同时迭代法对这q个迭代向量组进行迭代,并最终收敛到真实解。
q的取值为min(2p,p+8),需要注意的是初始迭代向量组的选取。一般取第一列全为1,从第二列开始,逐行取1,其余元素皆为0,例如下面这个向量组

细化后的子空间迭代流程为


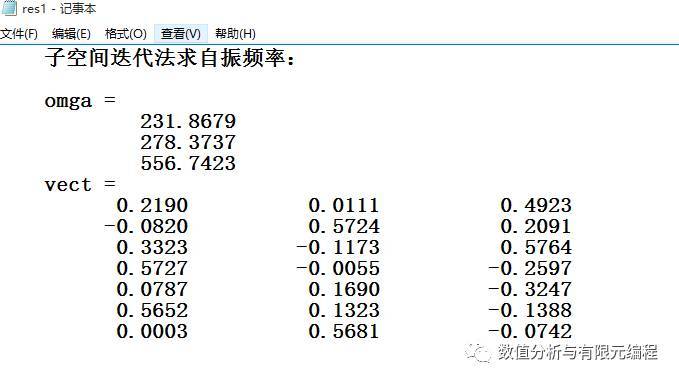
【例1】 如图所示的平面桁架,E = 2.0E11Pa,A = 1E-4m2,ρ=7300kg/m3,采用集中质量矩阵,用Fortran语言自编程序求得前三阶自振频率分别为 231.8679,278.3737,556.7423,与ANSYS计算结果一致。

PS:程序可在QQ群248687168下载
点击【阅读原文】查看广义特征值求解。
登录后免费查看全文
著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2024-04-01
最近编辑:7月前
相关推荐
热门文章