Lanczos算法求自振频率
Lanczos算法是一种基于瑞利-里兹方法的正交变换法,该方法在许多有限元软件得到了应用。例如ANSYS中模态分析就有Lanczos算法。
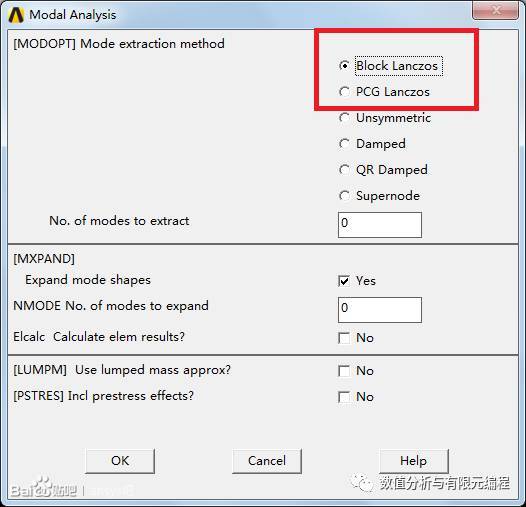
Lanczos基本算法流程:
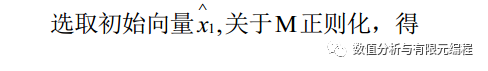

对i=2,3,...,q(q是欲求频率阶数),下列公式可形成一组关于质量矩阵M正则化得向量x1、x2、...xq
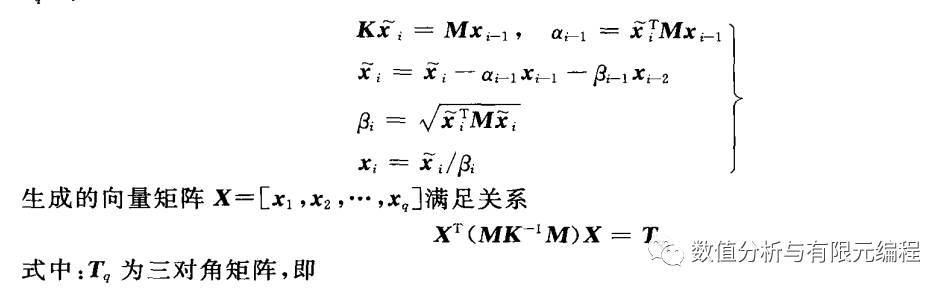
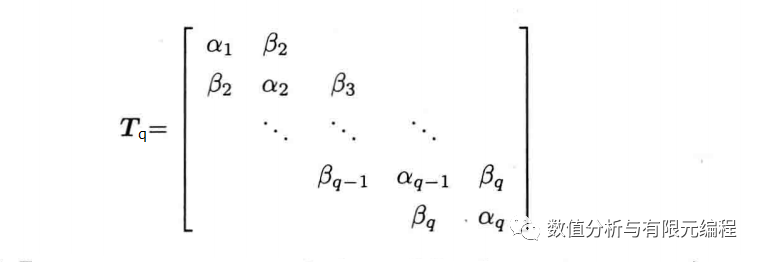

因此,矩阵Tq的特征值与Kφ= λMφ的特征值互为倒数关系。Tq是三对角矩阵,用QR迭代法或者Householder变换可高效地求解其特征值与特征向量。点击这里查看Householder变换
当q<n时,Lanczos算法可得出精确的低阶频率结果。为了提高其计算精度,需要对基本算法进行改进,比如在迭代过程中可以利用Gram-Schmidt技术对迭代向量进行重新正交化,采用移轴法提高效率等等。实际应用的Lanczos算法都是在上述基本算法基础上改进的。
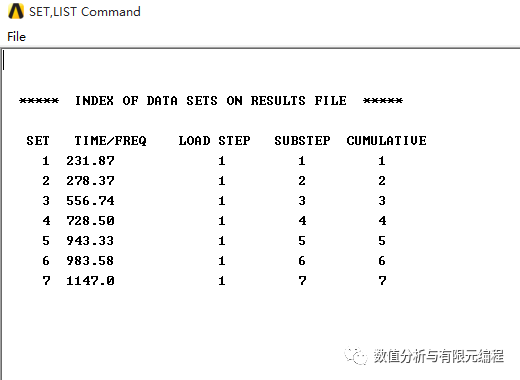
【例1】 如图所示的平面桁架,E = 2.0E11Pa,A = 1E-4m2,ρ=7300kg/m3,采用集中质量矩阵,用Fortran语言自编程序求得前两阶自振频率分别为 231.8679,278.3737,与ANSYS计算结果一致,而第四阶及以后频率的误差较大。这是算法本身的局限性。


登录后免费查看全文
著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2024-04-01
最近编辑:7月前
相关推荐
最新文章
热门文章