矢量函数
本文摘要(由AI生成):
本文介绍了函数w = f(x,y,z)在几何角度下的理解,它表示了如何将三维空间中的点与一个数值联系起来。函数可以是标量函数,如温度函数T(x,y,z),其输出是标量如温度。另外,还有矢量函数,如流体速度函数v(x,y,z),它表示在每个点的矢量,即大小和方向。矢量函数可以分解为沿坐标轴方向的分量,如空间中的力F(x,y,z)可以分解为x、y、z方向的标量函数。这些函数在物理和工程领域有广泛应用。
一个由三个变量组成的函数w = f(x,y,z)表示如何根据x,y,z来确定w的值。从几何角度更有利于对这个概念的理解:在空间笛卡尔坐标系下取一点,坐标为(x,y,z),函数w = f(x,y,z)告诉我们如何将一个点和一个数联系起来。例如:一个函数T(x,y,z)可以表明空间任意一点的温度。
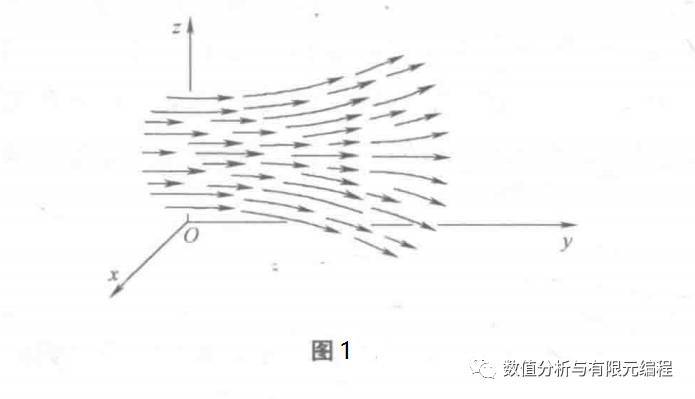
以上提到的函数f(x,y,z)和T(x,y,z)是标量函数,即在函数T(x,y,z)中给x,y,z赋值得到的结果是温度,温度是标量。矢量函数的一般形式简单明了。在三维空间中的一个矢量函数是一个将每个点(x,y,z)和矢量对应的法则,例如流体的速度。指定一个函数v(x,y,z),它表明了流体的速度和在这一点的流动方向。一般来说,一个矢量函数表明了在某个空间区域内每个点的大小和方向。可以利用许多箭头来描绘矢量函数的图像,如图1所示。在任一点处箭头的方向由矢量函数所确定,箭头长度和函数值大小成正比。
如图2所示,和矢量一样,矢量函数也能分解为几个分量。空间任意方向的力F(x,y,z)可以沿着坐标轴方向分解为
F(x,y,z)= Fx(x,y,z)i + Fy(x,y,z)j + Fz(x,y,z)k
其中Fx、Fy、Fz分别表示x,y,z方向的标量函数。

下面举一个矢量函数的例子:

PS:本文将矢量加粗以示区别。