矢量的一些应用(一)
本文摘要(由AI生成):
本文探讨了微积分在描述物理变量中的应用,特别是与牛顿力学相关的重要应用。微积分能够处理矢量的微分,对于理解速度和加速度的几何意义具有重要作用。文章详细解释了速度矢量的组成,并指出其在径向和切向两部分的表达。此外,文章还介绍了使用基底表示法来简化速度和加速度的计算,这在实际应用中非常方便。微积分的运用不仅在力学中有重要作用,同时也对数学本身产生了深远的影响。
量和微积分一样因牛顿力学的发展而应运而生,无论是对于力学和其他学科都有许多必不可少的应用,就是对数学本身也取得相当多的成就。下面就谈谈一些比较重要的应用:
(一)描述物理变量
在经典牛顿力学中,位置、速度、加速度以及所谓的力都是矢量,因此为了叙述经典的牛顿第二定律,必须要先给出矢量的微分。

因为速度矢量 V =dr/dt,如图1所示,注意 r =r*r0,其中 r 为 r 的长度,而 r0 为 r 的单位矢量。所以
V =(dr/dt)r0 +(dr0/dt)r
但由图可知, (dr0/dt) =(dθ/dt)θ0
因此
V =(dr/dt)r0 +(dθ/dt)rθ0,
而 θ0 是 r0 的横向(即与其正交)矢量的单位矢量。由此可见,速度矢量是由径向和切向两部分组成的。
这样的写法对于理解速度和加速度的几何意义的作用比较明显,但对于计算显然是很不方便的。若采取基底的表示法就比较容易了。比如将 r 表示为:
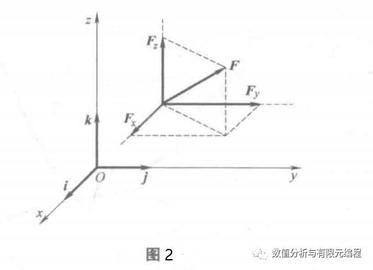
r =xi +yj +zk
则速度和加速度可表示为
V =dr/dt =(dx/dt)i +(dy/dt)j +(dz/dt)k

登录后免费查看全文
著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2024-04-01
最近编辑:7月前
相关推荐
最新文章
热门文章