三角形面积坐标
(一)三角形面积坐标的定义
三角形中任一点P与其三个角点相连形成三个子三角形,如图1所示
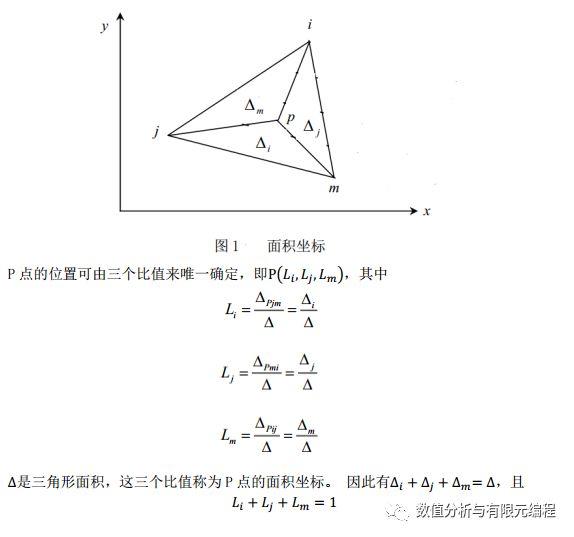
需要注意的是,这里引用的面积坐标,只限于用在一个三角形单元之内,在该三角形之外并无意义,因而是一种局部坐标.与此相反以前所用的直角坐标 x 和 y,则是总体坐标,它通用于所有单元,即通用于全结构。
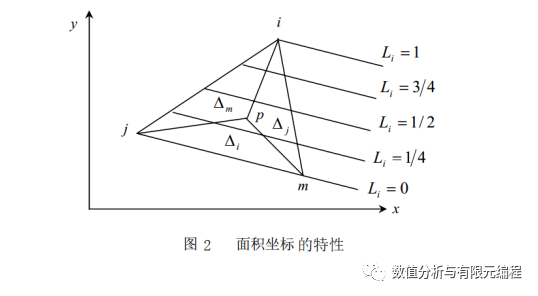
根据面积坐标的定义,由图2不难看出,在平行于jm边的直线上各点,其Li坐标值相同,对于平行于 ij,im 边的直线,也有同样性质。特别地,三角形单元上三个结点的面积坐标为

(二) 面积坐标和直角坐标的关系



(三) 面积坐标的微积分运算
结合式(6),根据复合函数的求导法则,有


对于高次三角形单元,若仍用直角坐标定义形函数,计算刚度矩阵将十分复杂;而改用面积坐标后,公式可大为简化且积分运算非常简单。
登录后免费查看全文
著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2024-04-01
最近编辑:1年前
相关推荐
最新文章
热门文章