力学概念| 直接传力路径
本文摘要(由AI生成):
本文讨论了增加结构刚度的三个概念,重点聚焦于传力路径对刚度的影响。文中提出,在结构中增加支撑体系可以优化传力路径,进而提升结构刚度。通过工程实例和计算分析,验证了优化支撑体系布置可以显著提高结构的侧向刚度,并指出基于概念的支撑布置可能更优化、合理。文章最后展示了超高层建筑支撑体系的布置案例,体现了实际应用中的效果。
提到了三个增加刚度的概念:
内力传递路径越直接,结构刚度越大。 内力分布越均匀,结构刚度越大。 内力越小,结构刚度越大。这三个概念具有普遍性,至少适用于梁系和杆系结构。
本文重点讨论传力路径对刚度的影响。
直接传力路径
力的自然属性是尽快传到支座。因此,只要有可能,主要传力路径就是接地的直杆。来看下面的例子。
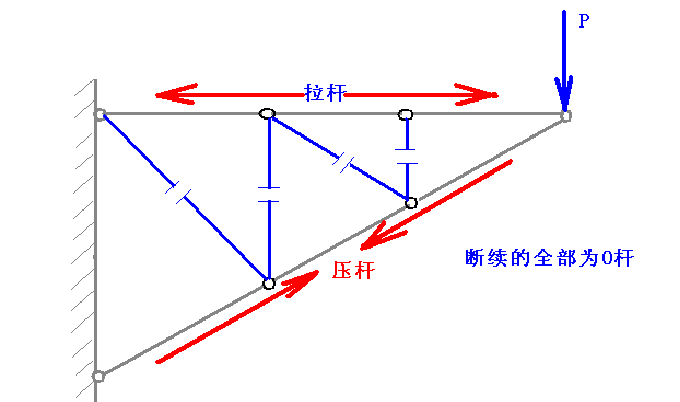
▲图0a 力的最短传递路径
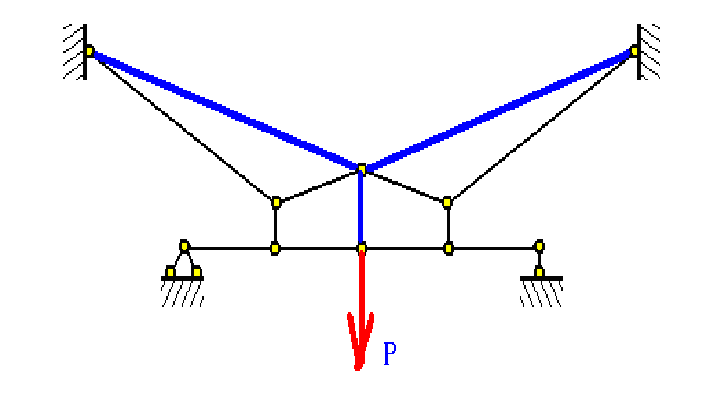
▲图0b 除了蓝色杆件外,其余为零杆
支撑体系
在结构中增加支撑体系是优化传力路径的办法。支撑体系的作用是保持结构稳定、传递荷载和提高结构侧向刚度。支撑杆件的布置方式多种多样,广泛应用于高层结构、脚手架结构和临时看台结构中。基于上述第一个概念并结合工程实例,可以得到四条用于布置支撑杆件的准则。这四条准则为
准则Ⅰ:由结构基础到顶部,每层都应设置支撑杆件。
准则Ⅱ:不同层间的支撑杆件应直接连接。
准则Ⅲ:支撑杆件应尽量以直线形式连接。
准则Ⅳ:顶层和其相邻跨间的支撑杆件应尽量直接连接。
准则Ⅰ是显而易见的,因为多层结构的控制节点在结构顶部,作用在顶部的荷载必然要传到结构支座。如果支撑杆件没有沿结构通高布置,则荷载传递效率会明显降低。准则Ⅰ可以通过多种方式来实现,而准则Ⅱ和准则Ⅲ则建议采用较短传力路径。前三条准则主要用于不同层间的支撑布置。对于那些跨数大于层数的结构,如临时看台,为了获得最短的传力路径和更多的零内力杆件(零杆),准则Ⅳ给出了布置不同跨间支撑杆件的方法。
考虑两个具有相同尺寸的四跨四层平面铰接结构,采用不同的支撑布置形式,如图1所示。所有杆件的材料和横截面面积均相同,水平和竖向杆件长度均为 。在每个接结构的两个角点上沿 方向作用有 的集中力,试确定这两个结构的位移。

▲图1 具有不同支撑体系的两个平面结构
这两个框架都是承受反对称荷载的对称结构,根据对称结构在反对称荷载作用下仅产生反对称内力的概念,可以取左半部分,利用节点处的平衡条件求出杆件内力。例如,结构 中第二跨与第三跨水平杆的内力一定为零,因为这两跨的内力是反对称的并且一定在中柱节点处平衡。这样,这两个结构中的所有杆件内力都可以较容易地通过手算得到,如图1c 和1d 所示。图中正值表示杆件受拉,负值表示杆件受压。
表1对两个结构的杆件内力进行了总结。其中第二行列出了不同的内力值,第三行是与不同内力值对应的杆件(单元)数目,第四行是相应杆件的 值, 是相同内力杆件的 之和。

▲表1
由表1可以看出:结构 的零杆比结构 的零杆多。结构 的最大最小内力差值比结构 的小。结构 的内力分布比结构 的均匀。由于结构 只满足准则Ⅰ,而结构 满前三条准则,因此根据开头的概念,结构 的刚度要比结构 大。表1中的最后一行给出了在相同荷载作用下两个结构的最大位移。换句话说,在两结构使用相同的材料且杆件数量相同条件下,结构 的侧向刚度是结构 的 倍(2916/7.657)。这验证了前面介绍的概念和准则的作用。
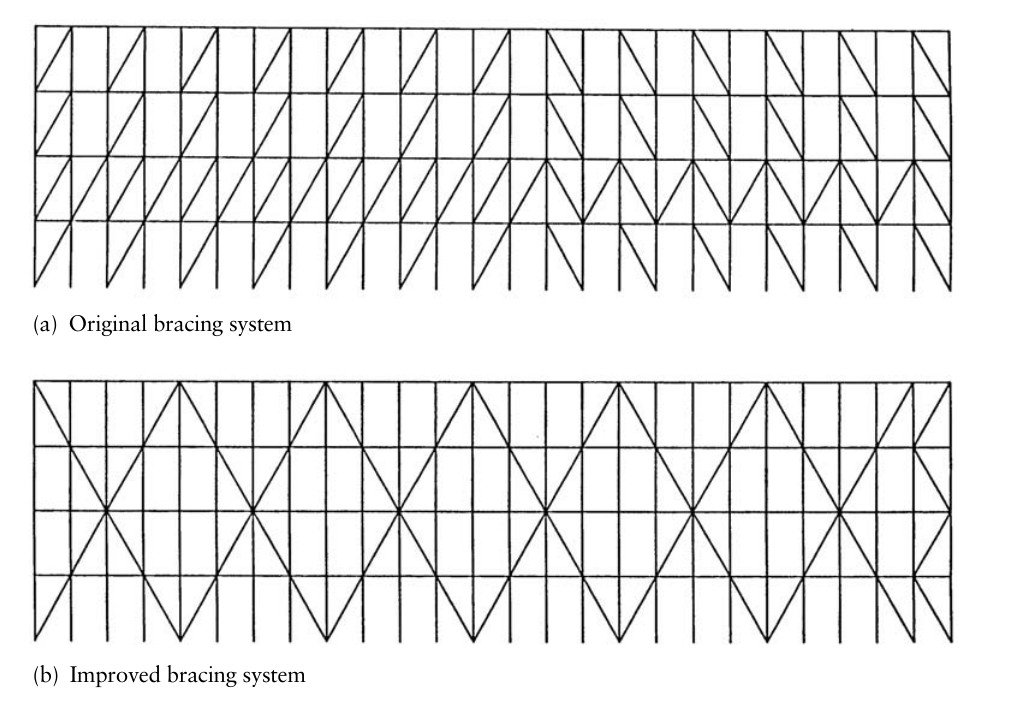
▲图2 临时看台的支撑布置形式
图2a所示为一个临时看台结构的后部支撑布置。支撑从底部到顶部隔跨布置,并在其余跨的第二层也布置了一道支撑。可以看出,这种支撑体系满足第一条准则,并且部分满足第三条准则。通过使用直接传力路径的概念,可以使看台的侧向刚度显著提高。对支撑杆件重新布置如图2b 所示。表2列出了对这两个结构侧向刚度的计算结果。对比结果表明,改进后结构的侧向刚度是原结构侧向刚度的284% 。不仅如此,改进后结构的支撑杆件减少了19%,因而比原结构更经济。此外,从两个框架的外观来看,改进后的支撑布置可能会感觉更美观。

▲表2
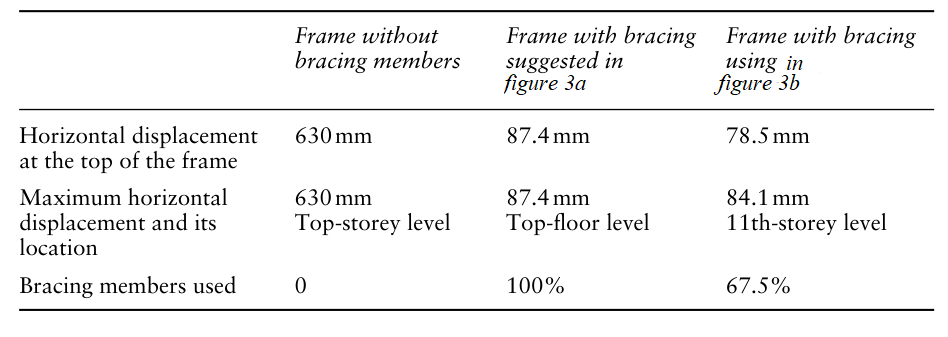
由于概念更具基础性,而且往往是针对结构整体的,因此高层结构中基于概念的支撑布置可能要比通过优化方法得到的设计更优化、合理。图3a所示是一个钢框架结构的支撑布置方案,此结果是基于拓扑优化理论获得,详见参考文献[1]。图3b是利用直接传力路径的概念(即前三条准则)设计的支撑体系。在支撑尺寸相同,荷载条件相同的条件下,计算得到两个框架的最大位移见表3所示。可以看出,利用概念所得的设计结果更实用、经济,且结构刚度更大。
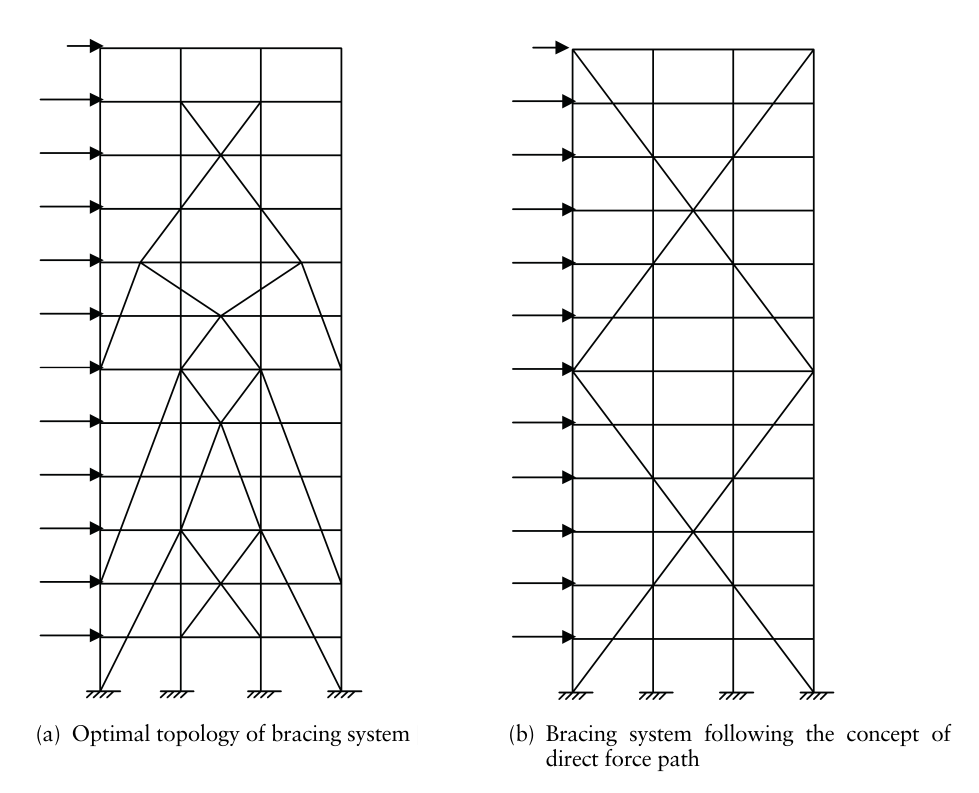
▲图3 支撑体系的设计对比
▲表3
以下是一些超高层建筑支撑体系的布置案例赏析。

▲深圳平安金融中心

▲天津117

▲广商中心
参考文献:
[1]Lian,Q., Xie, Y. and Steven,G.(2000) ' Optimal topology design of bracing systemsfor multi-story steel frames’, Journal of Structural Engineering, ASCE, Vol. 126, No. 7.
DOI: 10.1061/(ASCE)0733-9445(2000)126:7(823)





