力学概念 | 质心

本文摘要(由AI生成):
本文探讨了物体重心与稳定性的关系,指出重心低则物体稳定,重心偏移则可能引起倾覆。通过图1的动力学模型说明了结构刚度与自振频率的关系。文中以Kio双塔和CCTV新台址大楼为例,介绍了通过增加平衡配重和增大裙楼体量来降低质心、提高稳定性的方法。CCTV大楼的底板厚度和混凝土浇筑量也展现了工程技术的创新。文章还回顾了往期力学概念相关话题,为读者提供了丰富的力学知识。
重心是物体在重力作用下的平衡点或重力作用点。当物体的尺寸相对于地球足够小时,物体的重心与质心重合。
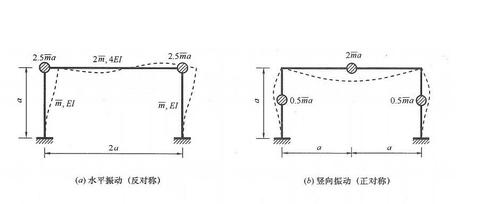
如图1所示,集中质量 越靠近支座,结构自振频率越大,说明总体刚度越大,抵抗变形的能力越强。

▲图1 单自由度动力学模型
物体的质心越低,物体越稳定,不倒翁就是一个例子。对于倾斜的高层建筑,建筑物的质心偏移,可能会引起建筑的倾覆作用。

▲图2 Kio双塔
图2所示为 “欧洲之门”Kio 双塔,高 ,共26 层,位于马德里市。Kio 双塔实际上是相互倾斜的,每个塔的竖向倾斜角为 。减小这种倾覆作用的措施之一是在建筑的地下室增加巨大的平衡配重。这种方法不仅能降低建筑物的质心,还能使建筑物的质心向基础中心的正上方移动。

▲图3 CCTV新台址大楼
图3所示为CCTV新台址大楼,主楼包括两座双向倾斜 的塔楼,连接两座斜塔楼顶部的14层高的悬臂结构,以及9层裙楼与三层地下室。1号塔楼有52层,屋顶最高处(停机坪)标高 ;2号塔楼46层,屋顶最低处标高 ;悬臂最大外挑距离 。该项目通过增大裙楼体量和基础筏板厚度来降低质心位置。裙楼体量明显比一些超过 的超高层建筑裙楼体量大。

▲图4 CCTV大楼底板厚度分布
塔楼一底板面积为 ,底板厚度为 不等,一次浇筑混凝土量为 。塔楼二底板面积 ,底板厚度为 不等,一次浇筑混凝量也超过 。无论是底板的厚度,还是一次连续浇筑的混凝土量,在目前国内外房建施工中,都是前所未有的。在CCTV大楼附近,高度为 的中国尊基础底板最厚才 。

▲图5 中国尊
★★★★★★★ 往期 ★★★★★★★★