力学概念 | 利用对称性原理巧解一道结构力学题_燃料电池_多学科优化

力学概念 | 利用对称性原理巧解一道结构力学题

8月前浏览10358

本文摘要（由AI生成）：

本文探讨了超静定桁架中特定杆的轴力求解问题。针对结构对称性和荷载分布特点，作者提出通过利用对称性简化计算过程的方法。文中分析了桁架下弦杆件轴力为零的原因，并展示了通过去掉中间弹簧约束得到的基本结构。在此基础上，利用力法方程快速求解其余各杆的轴力。文章还展示了荷载作用在基本结构上的情况，并给出了各杆轴力的求解方法。此外，文章还提供了往期力学概念的相关内容，为读者提供了丰富的力学知识。

如图1所示的超静定桁架，已知为常数，弹簧刚度，求杆的轴力。

▲图1

分析：该结构是二次超静定问题，常规思路需要去掉2个约束，这样一来计算量很大。但是，本题结构对称，荷载也对称分布，可以充分利用对称性。对于对称轴上的杆来说，只要竖向荷载对称，杆就只能竖直下沉，点不会向左或者向右偏移，点亦是如此。另一方面，两个支座把桁架的下弦的左右两端固定，因此下弦的4个杆件轴力皆为0。这个结论对于上弦不成立，因为上弦左右两端没有固定。有了上述的结论，只需去掉中间弹簧这一个约束也能快速解出来。

▲图2

基本结构如图2所示，力法方程为

已知下弦各杆轴力为0后，能快速得到其余各杆的轴力。

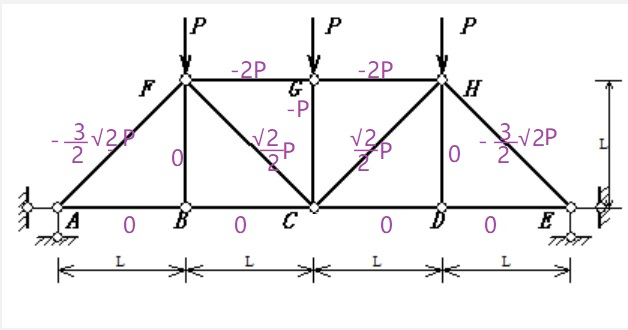
▲图3

如图3所示，荷载作用在基本结构上，各杆轴力也可快速得到。

★★★★★★★ 往期 ★★★★★★★★

力学概念 | 利用对称性原理巧解一道结构力学题
 力学概念 | 集中质量法求自振频率

来源：数值分析与有限元编程

有限元知识| 沙漏、零能模式

本文摘要（由AI生成）：沙漏现象发生在采用一阶、减缩积分单元时，由于单元只有一个积分点，周边节点变形随意，导致单元过于柔软。解决方法包括合理细化网格、避免点荷载，以及在大应变区使用一阶单元。而零能模式是一阶减缩积分时出现的问题，单元在受弯时积分点无应变能，失去刚度，无法抵抗变形。解决方法可以是提供人工“沙漏刚度”或细化网格，确保在高度方向至少4个单元。沙漏（hourglassing）沙漏简单地说就是单元只有一个积分点，周边的节点可以随意变形。发生的对象：一阶、减缩积分单元；产生的结果：单元太柔；解决方法：1.对一阶减缩单元，合理细化网格；荷载避免使用点荷载； 2.在大应变区或大应变梯度区使用一阶单元，而不是使用二阶单元。零能模式（zero-energy mode）采用一阶减缩积分时会出现零能模式。即单元只有一个积分点，在受弯时该积分点没有任何的应变能，此时此单元没有任何刚度，就无法抵抗变形。解决方法：1.提供人工的“沙漏刚度”；2.细化网格（一般在高度方向至少要有4个单元）来源：数值分析与有限元编程