《有限元基础编程百科全书》| 杆单元(1D、2D、3D、变截面、直接刚度法、数值积分求解)
本文摘要(由AI生成):
本文主要介绍了杆单元类型,包括1D杆单元、变截面杆单元、2D杆单元和3D杆单元。杆单元类型主要围绕一个受到外力拉伸的拉杆模型展开,激发读者"举一反三"的学习兴趣。单元描述中,一维杆单元每个节点1个自由度,表示 方向的平动位移;二维杆单元每个节点两个自由度,表示 、 两个方向的平动位移;三维杆单元每个节点3个自由度,表示 、 、 三个方向的平动位移。单元内部的位移与节点位移通过"形函数"联系起来,单元刚度矩阵可通过坐标变换得到。最后,文章还提供了数值案例和应力场、位移场、应变场等结果。
杆件是最常用的承力构件,它的特点是连接它的两端一般都是铰接接头,因此,它主要是承受沿轴线的轴向力,因两个连接的构件在铰接接头处可以转动,则它不传递和承受弯矩。

上图所示,是一左端固定,右端拉伸的受到外力 拉伸的拉杆模型。杆件长度为 ,弹性模量为 ,截面面积为 ,假设为等截面杆(变截面杆模型后续会提及)。
本节将为读者分享以下杆单元类型:
1D杆单元 变截面杆单元 2D杆单元 3D杆单元
以上的杆单元类型都将围绕上图所示的模型展开,激发读者"举一反三"的学习兴趣。
单元描述
一维杆单元每个节点1个自由度,表示 方向的平动位移;二维杆单元每个节点两个自由度,表示 、 两个方向的平动位移;三维杆单元每个节点3个自由度,表示 、 、 三个方向的平动位移,模型自由度示意图见下图。
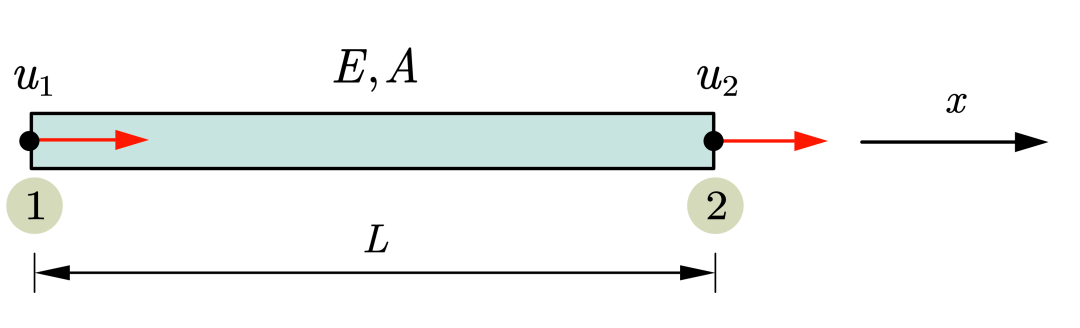



单元内部的位移与节点位移通过"形函数"联系起来,见下式, 表示单元内部任意一点的位移, 表示节点位移, 为形函数矩阵。
单刚矩阵
公式推导
以一维杆单元为例,单元刚度矩阵可直接使用:
、 、 分别表示该单元的弹性模量、截面面积、单元长度。有关具体推导过程,可翻阅任意有限元教材,都会基于最小势能原理进行讲解,本文不再赘述,只挑一些对我们数值编程有直接作用的。
变截面杆单元顾名思义就是单元截面会发生变化,假设单元两端的截面面积不一致。其单元刚度矩阵可表示为:
二维、三维杆单元的刚度矩阵均可以由一维杆单元刚度矩阵演变而来,其基本思想就是坐标转换。以二维为例:
局部坐标系下的单元节点位移:
全局坐标系下的单元节点位移:
局部坐标可由全局坐标经过坐标变换得到:
矩阵形式:
其中
其刚度矩阵也可由局部坐标系下的刚度矩阵通过坐标变换得到:
其中,
三维杆单元的坐标变换矩阵:
相关代码
function [BarLength]=BarsLength(x,y,ele)
BarLength=zeros(size(ele,1),1);
for iEle =1: size(ele,1)
BarLength(iEle,1)=((x(ele(iEle,2))-x(ele(iEle,1)))^2+(y(ele(iEle,2))-...
y(ele(iEle,1)))^2)^0.5;
end
end
function [R]=CoordTransform(x,y,BarLength)
l=(x(2)-x(1))/BarLength; m=(y(2)-y(1))/BarLength;
R=[l m 0 0;0 0 l m];
end
function [Ke] = BarElementKe(prop,R,BarLength)
E = prop(1);A = prop(2);
ke=A*E/BarLength*[1 -1;-1 1];
Ke=R'*ke*R;
end
也可使用数值积分方案来计算单元刚度矩阵,具体原理将在介绍平面单元时讲解。
function ElementStiffnessMatrix = gaussIntegrate2DBarElement(prop, R,L)
E = prop(1);A = prop(2);
gaussPoints = [-1/sqrt(3), 1/sqrt(3)];
weights = [1, 1];
K = zeros(2, 2);
for i = 1:length(gaussPoints)
xi = gaussPoints(i);
w = weights(i);
dN_dxi = [-1/2, 1/2];
J = L / 2;
B = dN_dxi / J;
k = w * (B' * E * A * B) * J;
K = K + k;
end
ElementStiffnessMatrix = R'*K*R;
end
数值案例
本小节结合二维的桁架结构和三维桁架结构,分别施加"力加载"和"位移加载"两种加载方式。将自编有限元程序结构和Abaqus分析结果进行对比,保证程序的正确性,程序采用Abaqus进行前处理+Matlab内核计算+ Paraview进行后处理。
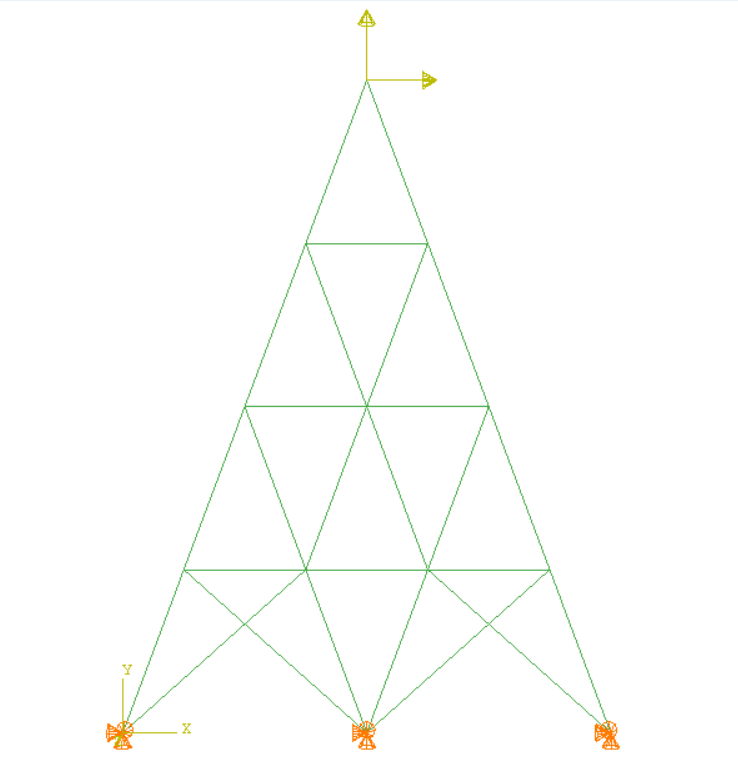

二维模型边界条件信息:
## 位移加载信息
*Constr
1,2,4.
1,3,-1.
2,2,4.
2,3,-1.
233,1,0.
233,2,0.
233,3,0.
...
## 力加载信息
*Load
1,2,400.
1,3,-100.
2,2,400.
2,3,-100.
*Constr
233,1,0.
233,2,0.
233,3,0.
...
三维模型边界条件信息:
## 位移加载信息
*Constr
1,2,4.
1,3,-1.
2,2,4.
2,3,-1.
233,1,0.
233,2,0.
233,3,0.
...
## 力加载信息
*Load
1,2,400.
1,3,-100.
2,2,400.
2,3,-100.
*Constr
233,1,0.
233,2,0.
233,3,0.
...
数值结果
通过将自主开发的有限元程序与Abaqus软件的场变量结果(包括位移、应力、应变等)进行比较,对比结果表明两者具有较高的一致性。此一致性验证了自编程序在计算精度方面的准确性。
位移场
力加载

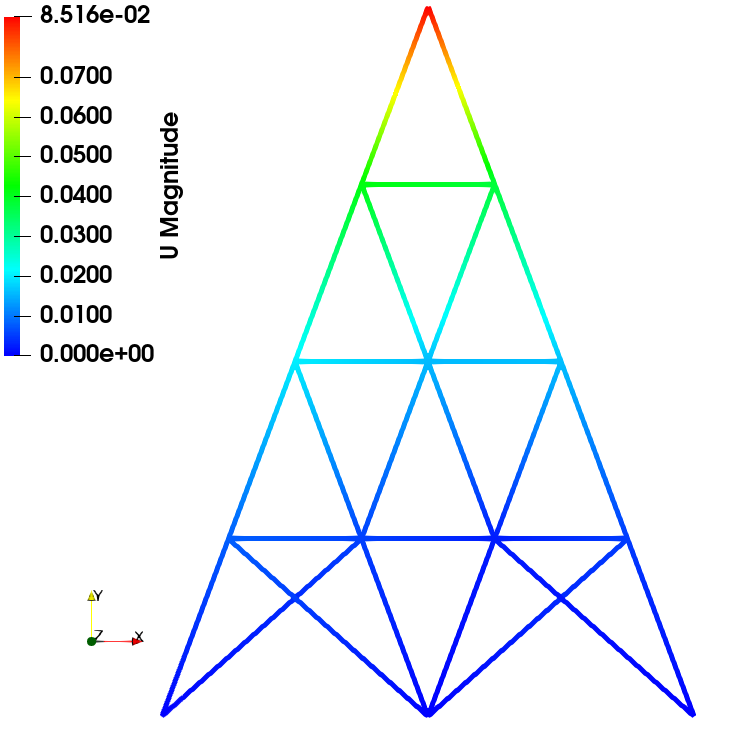

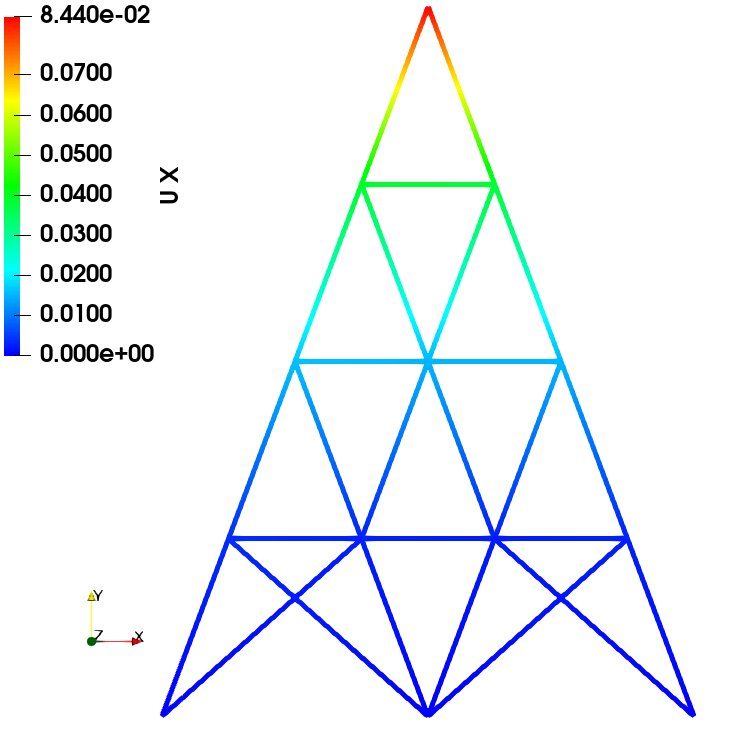

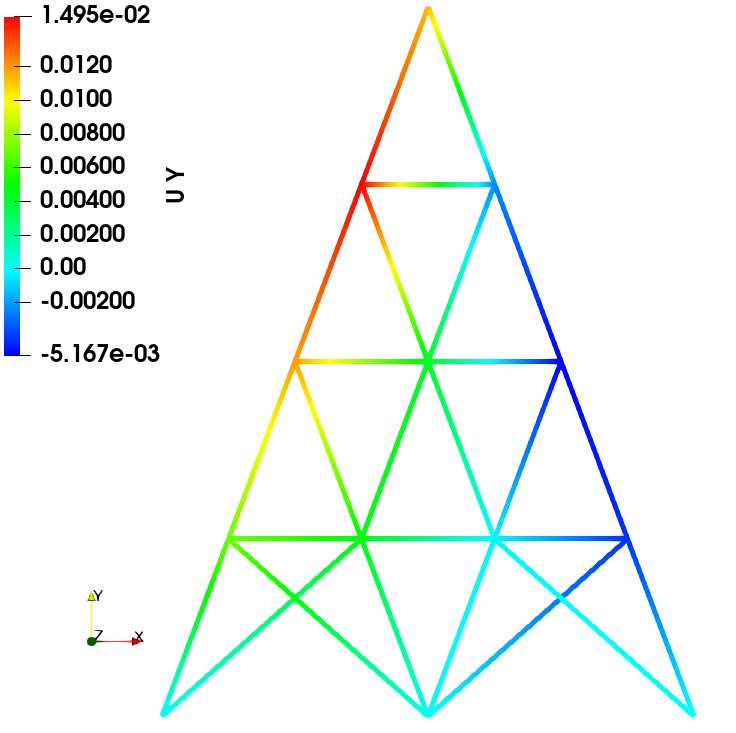
位移加载
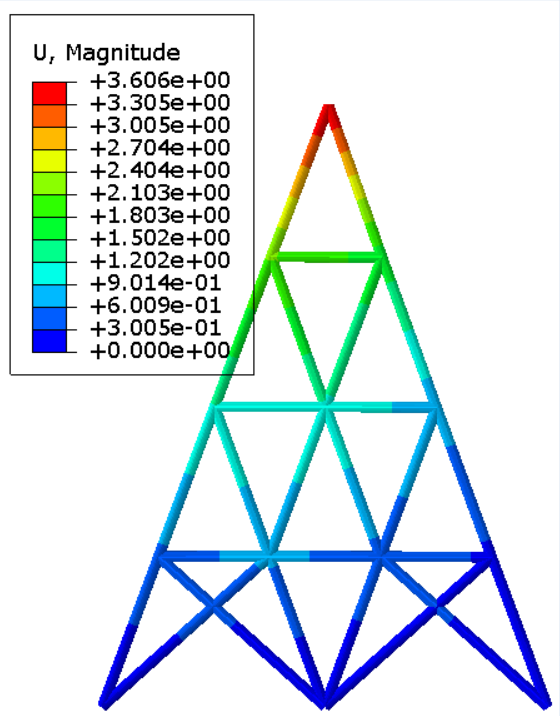


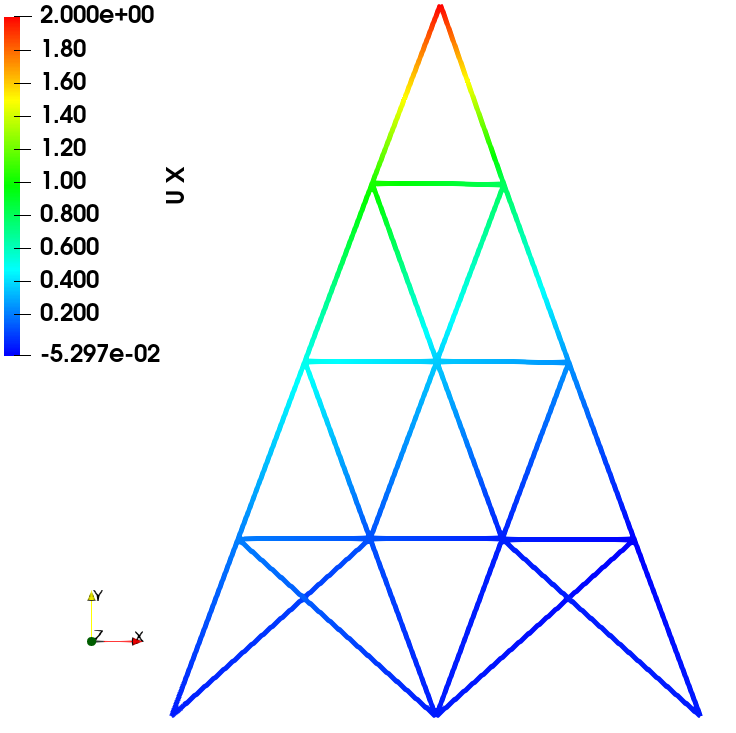
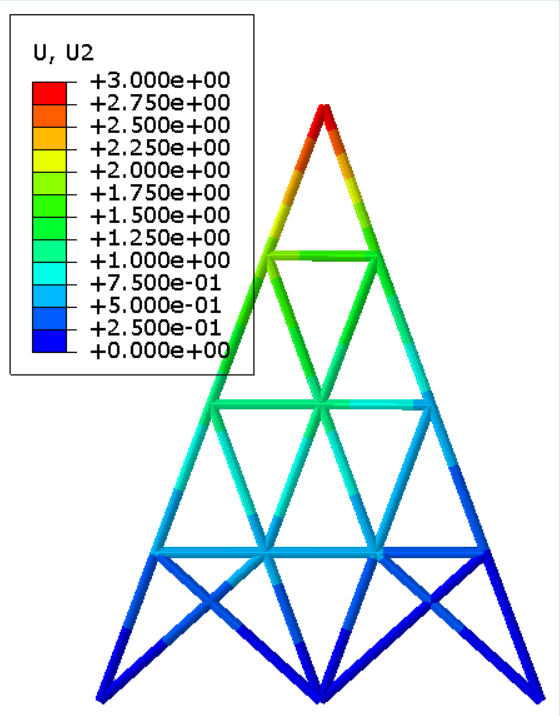
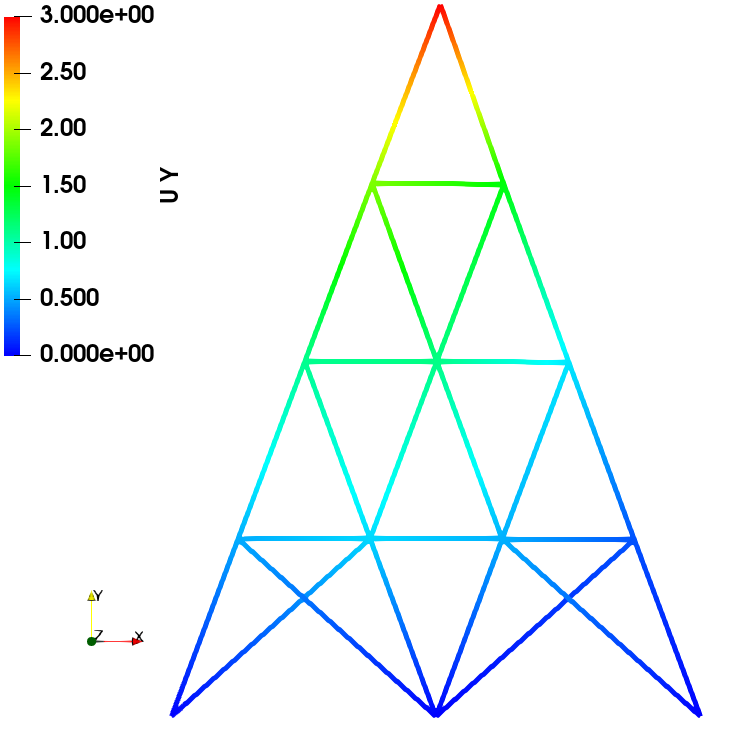
应力场
力加载
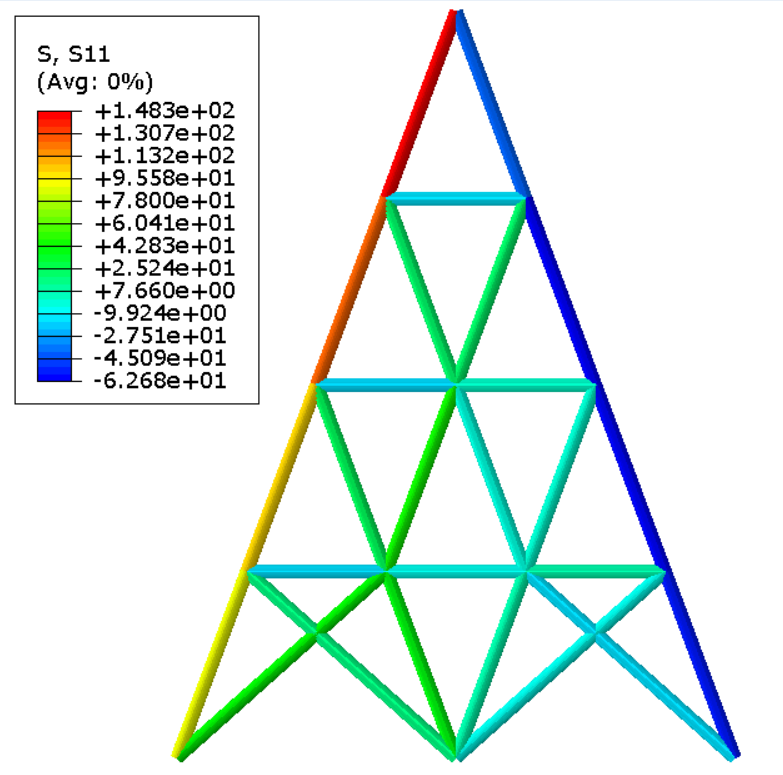
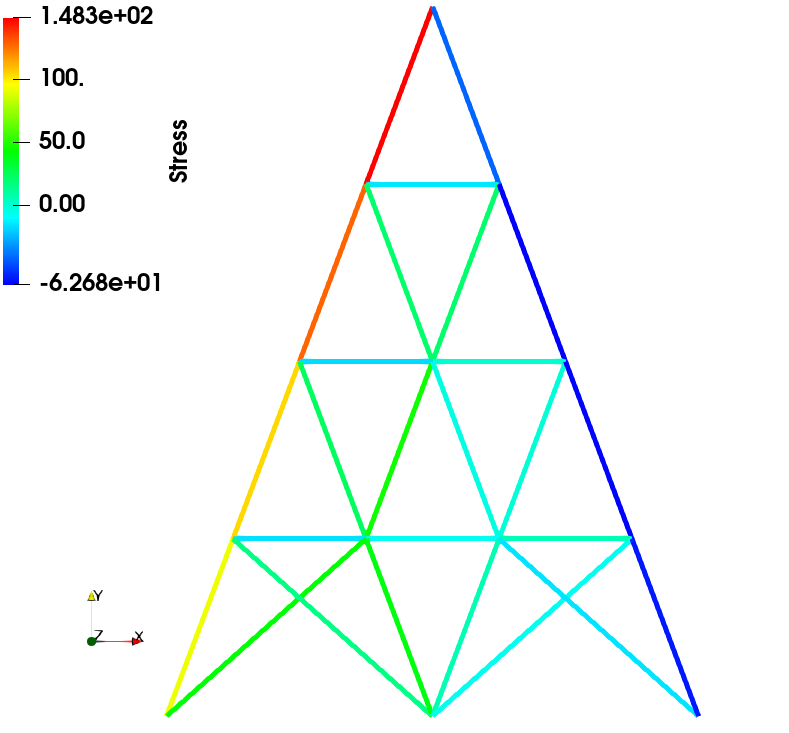
位移加载


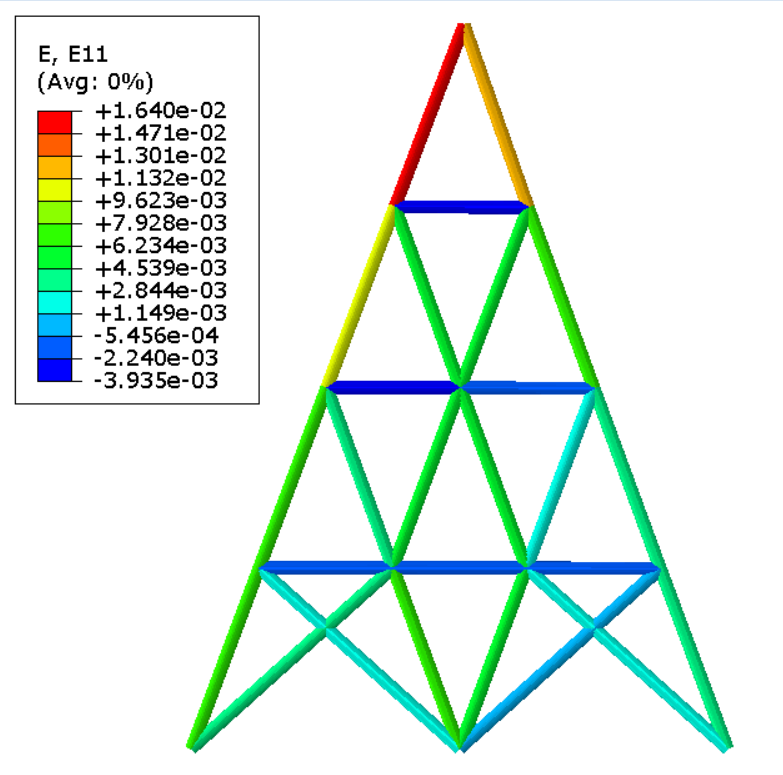
应变场
力加载
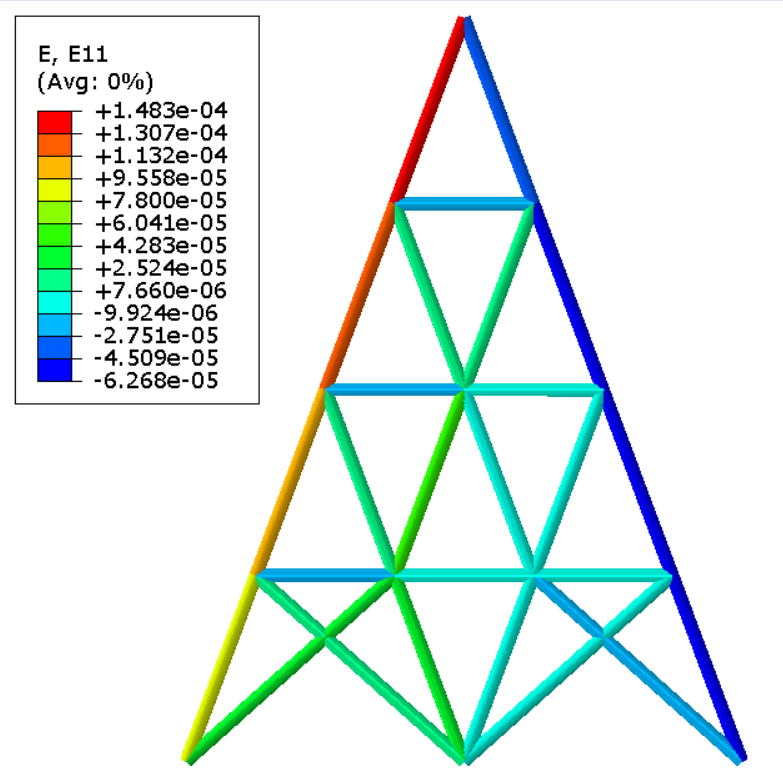

位移加载

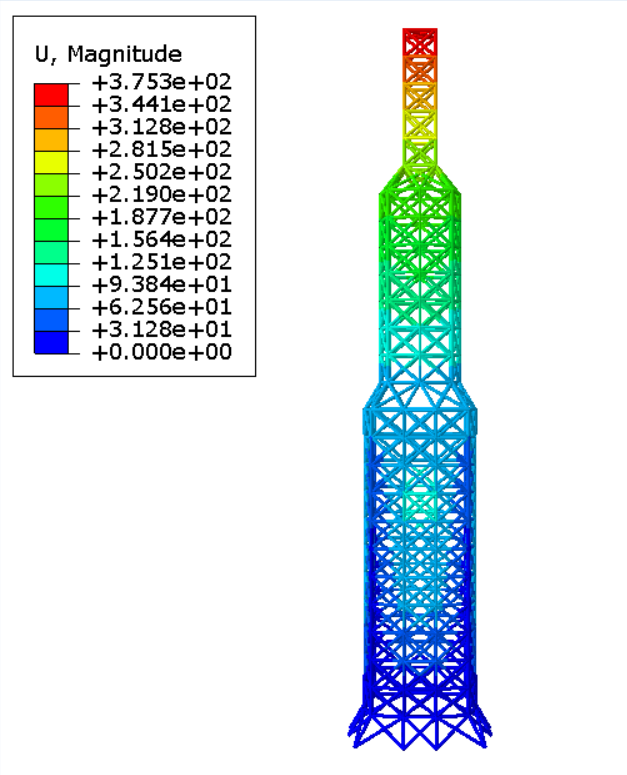
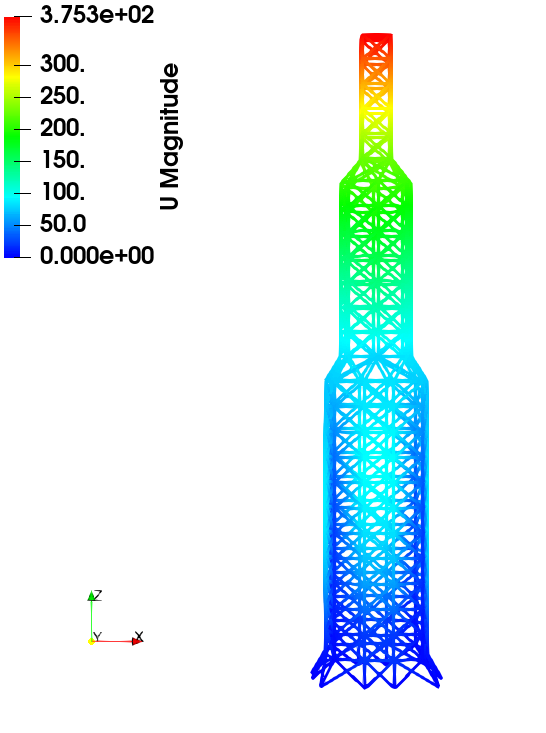
三维模型位移场
力加载
位移加载
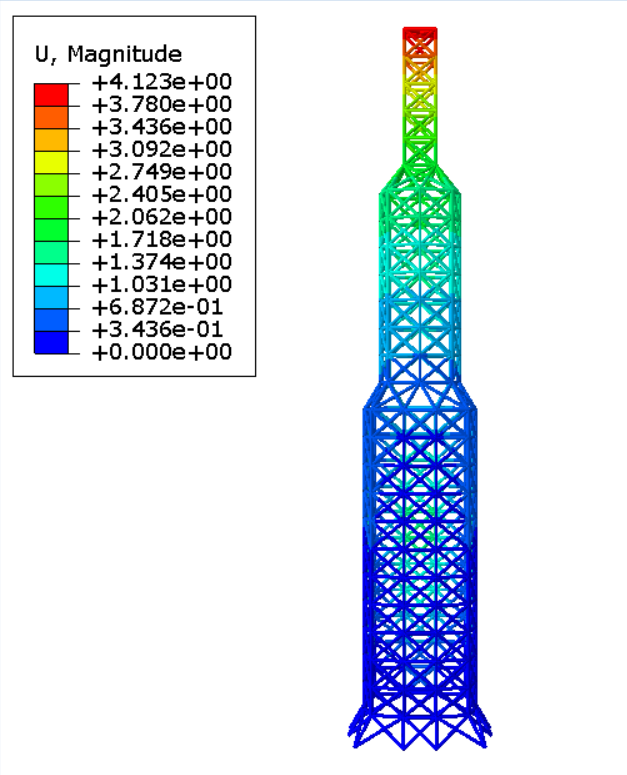

为节省篇幅,三维模型仅对比位移场,其余场变量读者可自行对比验证。
以上整套程序均在《有限元基础编程百科全书》中,以超链接的形式呈现。


