数学之美-公式的图形化
本文摘要:(由ai生成)
本文介绍了如何利用MATLAB软件绘制数学图形,展示了12个示例脚本,包括三维心形函数、极坐标图等。通过调整参数,可以生成多种理工科常见的数学图形,如心形图案、螺旋线等。图形注释简洁明了,便于读者理解。这些示例适用于对数学可视化感兴趣的学生和研究人员,有助于直观理解数学概念和欣赏数学之美。
相信很多小伙伴都了解“数学”在探索真理过程中的作用,小编自初中时代就听说了“数学”的伟大,伟大的科学家、哲学家同时还有一个共同的身份-“数学家”,而在人类历史发展和社会生活中,数学也发挥着不可替代的作用,也是学习和研究现代科学技术必不可少的基本工具。
提到数学,不得不说一款学习并理解数学的利器-MATLAB。相信众多的研究僧们在查阅文献的时候都看到了文献中精美的图片,自己却不知如何绘制。在此,小编采用MATLAB强大的绘图功能将12个公式几何化,同时列出了图形绘制程序,将数学之美可视化。
1.理工男的烂漫-三维心
clc;clear;close all;
colormap('flag');
n=100;
x=linspace(-3,3,n);
y=linspace(-3,3,n);
z=linspace(-3,3,n);
[X,Y,Z]=ndgrid(x,y,z);
F=(X.^2+(9/4).*(Y.^2)+Z.^2-1).^3-X.^2.*Z.^3-(1/9).*Y.^2.*Z.^3;
isosurface(F,0)
lighting phongcaxis;
axis equal
view([55 34]);
title('旋转的心形_三维心形函数')
axis off
while 1
rotate(F,[0,0,1],3);
drawnow
end

2
clc;clear;close all;
s=0:0.1*pi/180:7200*pi/180;
g=(exp(1)).^(sin(s))+2.*cos(s)+(sin(49*s)).^4;
plot(s,g);
polar(s,g,'-r')

3
clc;clear;close all;
t=0:0.1*pi/180:7200*pi/180;
r=(exp(1)).^(cos(t))-2.*cos(4*t)+(sin(t/12)).^5;
%plot(t,r);
polar(t,r,'-r')
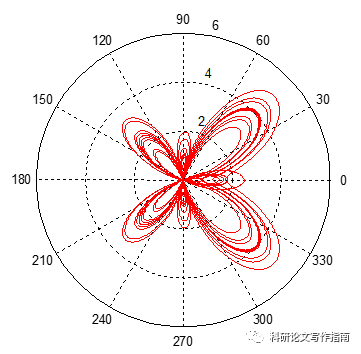
4
clc;clear;close all;
t=0:0.1*pi/180:72000*pi/180;
%r=(exp(1)).^(cos(t))-2.*cos(4*t)+(sin(t/12)).^5;
%plot(t,r);
r=2+8*cos(5*t);
polar(t,r,'-r')

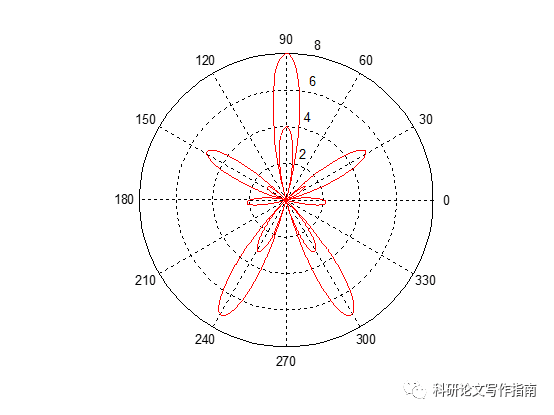
5
clc;clear;close all;
t=0:0.1*pi/180:360*pi/180;
%r=(exp(1)).^(cos(t))-2.*cos(4*t)+(sin(t/12)).^5;
%plot(t,r);
%r=2+8*cos(5*t);
r=2*(1-3.*sin(t)).*cos(6*t);
polar(t,r,'-r')
6
clc;clear;close all;
t=0:0.1*pi/180:560*pi/180;
%r=(exp(1)).^(cos(t))-2.*cos(4*t)+(sin(t/12)).^5;
%plot(t,r);
%r=2+8*cos(5*t);
%r=2*(1-3.*sin(t)).*cos(6*t);
r=4.*cos(t.^0.5)-6.*sin(t.^0.5)+3;
polar(t,r,'-r')

7
clc;clear;close all;
t=0:5*pi/180:360*pi/180;
r=8*sin(100*t);
polar(t,r,'-r')

8
clc;clear;close all;
t=0:1*pi/180:2*pi;
x=-1-cos(t);
x0=1+cos(t);
polar(t,x,'-pr');
hold on;
polar(t,x0,'-pr');

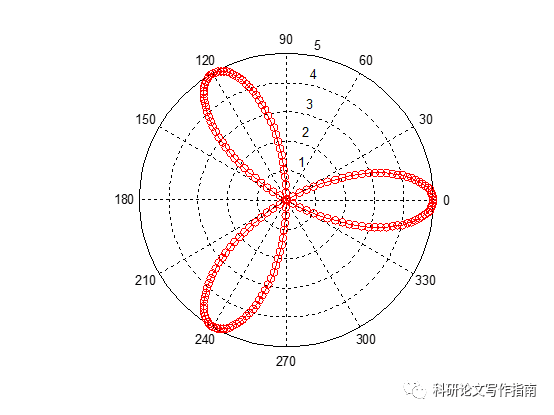
9
clc;clear;close all;
t=0:1*pi/180:2*pi;
a=5;
p=a*cos(3*t);
polar(t,p,'-or');
10
clc;clear;close all;
t=0:1*pi/180:2*pi;
p=2-2.^sin(5*t);
polar(t,p,'-or');

11
clc;clear;close all;
t=0:0.1*pi/180:20*pi;
r=sin(2*t);
s=cos(11*t);
polar(s,r,'-r');

12
clc;clear;close all;
t=0:0.1*pi/180:20*pi;
r=sin(2.334*t);
s=t-1;
polar(s,r,'-r');






