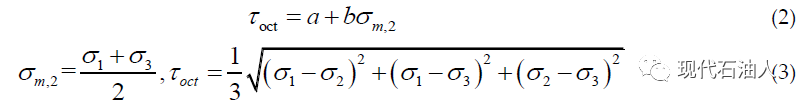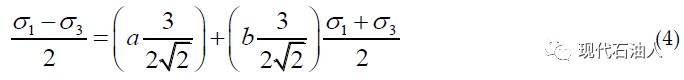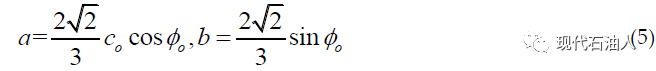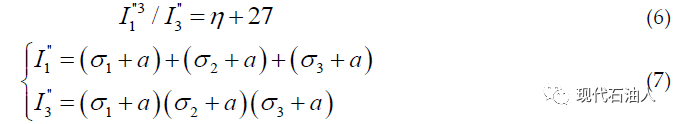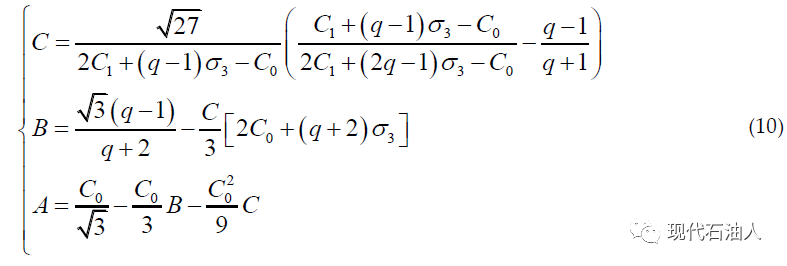本文摘要:(由ai生成)
岩石强度准则是预测岩石极限强度的理论基础,Mohr-Coulomb和Hoek-Brown准则常用但忽略中间主应力影响。为更精确描述岩石破坏行为,发展了基于这两准则的三维强度准则,考虑Lode角对强度的影响。文章介绍五种基于MC的三维强度理论,并通过数值分析软件展示它们与经典MC准则的区别。为获得更准确的预测结果,应综合使用多种方法预测与监测地层压力。
岩石强度准则是判断岩石在不同应力状态下,是否会发生屈服或破坏的理论,常用于预测不同应力状态下岩石的极限强度。目前,最常用的、影响最深远的是Mohr-Coulomb准则和Hoek-Brown准则,但是这两个经典的强度准则未考虑中间主应力的影响,仅描述岩石在三轴压缩状态下的极限强度。
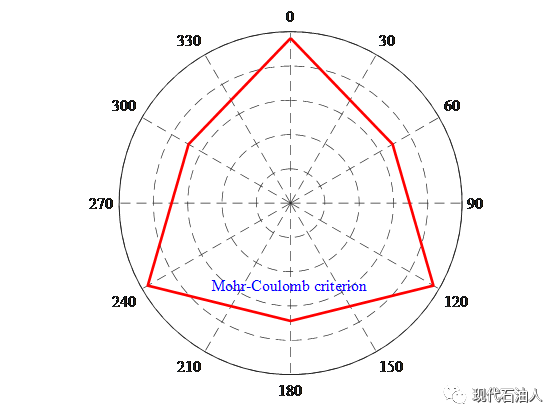
几个世纪以来,岩石力学工作者对多轴应力状态下岩石屈服与破坏特征及理论开展了大量研究,依据MC和HB准则建立了很多三轴应力状态下的强度准则。考虑三轴应力的强度准则可以区分三轴压缩和三轴拉伸应力状态岩石破坏强度的区别,也就是说三轴强度准则可以反映Lode角对岩石强度的影响。小编将岩石的三维强度准则分为两类,基于MC准则的三维强度准则和基于HB准则的三维强度准则两大类。本节内容,小编整理了五种基于MC准则的内聚力和内摩擦角概念建立的三维强度理论,分别为不考虑中间主应力影响的Mohr Coulomb准则、Modified Lade准则、Modified Wielbols Cook准则以及Mogi Coulomb准则。此处,小编采用数值分析软件绘出了以上几种准则在三大主应力空间的极限面及在偏应力平面的极限迹线,为对比三维强度准则与经典的MC准则的区别,同时绘出了MC的极限迹线,关注现代石油人公 众 号获取更多石油工程科研资料分享。赞赏后可得Mohr-Coulomb准则在三轴应力空间极限面和偏应力平面极限迹线的计算程序,并提供免费指导服务,感谢您的支持,为小编加个鸡腿!以上几种准则的方程式、分布特征及数值模拟程序如下,库仑(1773)持岩在任一平面的剪应力超过岩体的黏聚力和摩擦力时就会发生破坏。1900年,莫尔用图形系统地说明了这种破坏,自此该准则在岩石破坏预测中被广泛接受,称为莫尔-库仑准则。用σ1和σ3表示:
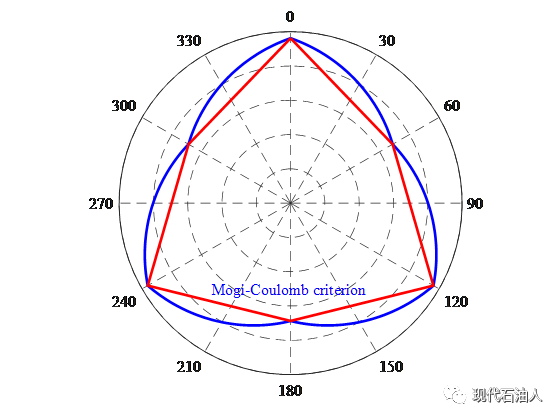
Mogi(1971)对不同的岩石岩性进行了一定数量的多轴实验,基于精确的数据集,Mogi提出了这样一个假设:作为摩擦力的畸变应变能与八面体剪应力τoct成正比,σm,2随着σm,2的增大而增大,直到达到峰值强度的临界水平。基于这一结果,Al-Ajmi和Zimmerman(2005)发现了一个线性关系,可以很好地拟合τoct-σm,2空间的多轴试验数据,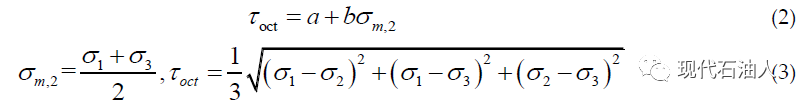
线性Mogi-Coulomb准则(MGC)与常规三轴应力状态下的Mohr-Coulomb等效,当σ1>σ1=σ1时,式(2)可表示为:
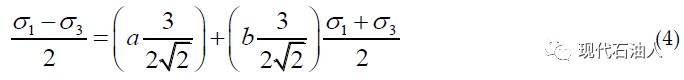
将式(4)与式(1)比较,参数a、b可由黏聚力、内摩擦角确定,
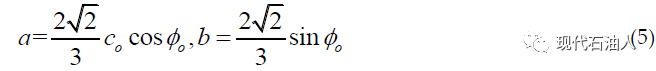
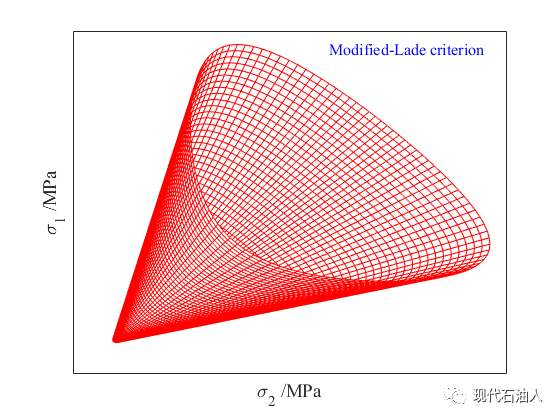
Lade(1977)在实验观测的基础上,提出了无粘性土的强度模型,称为Lade准则。该模型考虑了应力不变量对屈服和破坏的影响,剪切膨胀与大气压力呈非线性关系,而对于除岩石外的无粘性介质则定义了该模型。Ewy(1999)引入参数S作为黏聚力的函数,将Lade准则推广到岩石力学应用,即修正Lade准则(ML),
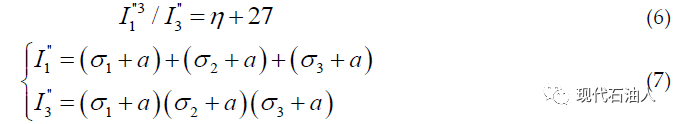
强度常数S和η与Mohr-Coulomb准则参数(黏聚力和内摩擦角)的关系可由式(8)得到。

如前所述,co和可以根据三轴实验或测井资料进行评价,因此可以方便地得到S和η。Wiebol andCook(1968)通过对滑动裂纹的细观力学分析得出,当微裂纹封闭的剪切应变能达到临界水平时,岩石就会发生破坏,提出了考虑中间主应力的wiebol -Cook判据。1994年,Zhou提出了一个非线性准则,该准则是对受限Drucker - Prager模型的扩展,由于其数学形式与Wiebols-Cook准则相似,因此被称为Modified Wiebols-Cook准则(MWC)。  其中,J1为平均有效围压应力,J2为第二不变偏压应力。强度常数A、B和C的表示形式如下:
其中,J1为平均有效围压应力,J2为第二不变偏压应力。强度常数A、B和C的表示形式如下:
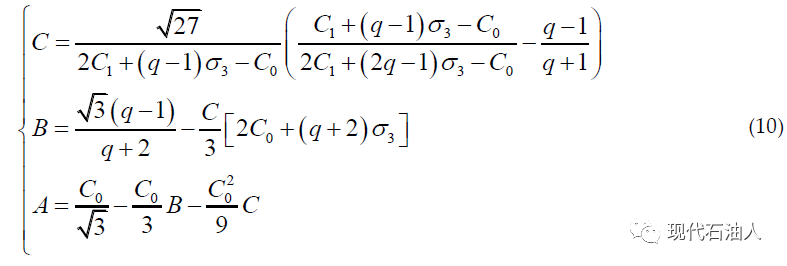
式(10)中所含参数可由黏聚力和内摩擦角确定,其关系为:

最后,根据偏应力空间变量,摩尔-库仑准则可以改写为:

Lee等人(2012)用Jiang and Pietruszczak(1988)提出的凸光滑形状函数gJP(θ)代替形状函数gMC(θ),  在该式中,当k接近0.5时,其横截面成为曲线三角形,而k接近1时,其横截面为圆形,Lee etal.,(2012)将MC准则推广到其应力维数。K为三轴拉伸破坏时ρ值与三轴压缩值的比值,可以表示为:
在该式中,当k接近0.5时,其横截面成为曲线三角形,而k接近1时,其横截面为圆形,Lee etal.,(2012)将MC准则推广到其应力维数。K为三轴拉伸破坏时ρ值与三轴压缩值的比值,可以表示为:
介绍完以上五种岩石强度准则的后,下面用图形展示这五种准则在不同的应力空间中的分布特征,