铺层复合材料HyperMesh建模及优化——从经典层合板理论说起

导读：

《铺层复合材料HyperMesh高级建模及OptiStruct仿真优化》是笔者在仿真秀平台原创的复合材料建模分析优化首套视频教程，详情见文后。它深度讲解：基于HyperMesh铺层复合材料建模流程，板类建模，工字梁类建模；基于OptiStruct铺层复合材料仿真及设置，复合材料失效准则，复合材料相关输出；基于OptiStruct铺层复合材料优化，铺层形状优化，铺层厚度优化，铺层顺序优化。

一、写在文前

本文是基于前文的更新。前文发表后，根据读者反馈，文中有些错误和不妥之处，故更新为本文，感谢大家的支持。

在此，特别感谢美国普渡大学余文斌教授的指点，他指出的目前层合板理论中的缺陷及我们常规教材中的错误，对本人的触动很大。在本文的末尾，会引用余文斌教授文章中的观点，希望能有更多的从事复合材料行业的同仁看到。

复合材料属于各向异性材料，与传统金属材料在力学性能分析方面有很大的不同，同时复合材料的多组分结构特征造成了在结构分析方面的复杂性。

复合材料的范畴很广，广义上讲，我们能够看的材料都是复合材料。但我们实际应用中已经把复合材料的范围框在了一个很小的范围，比如纤维增强复合材料。根据纤维长度，又可以分为长纤维和短纤维，长纤维中用的最多的就是长纤维铺层复合材料。

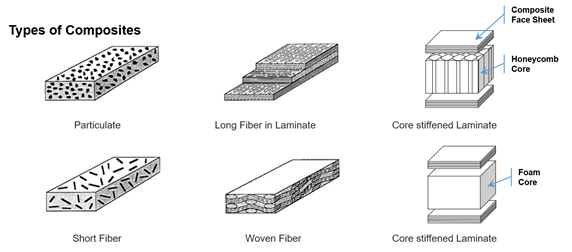
经典层合板理论，Classical Laminate Theory ，简写CLT，是一种常用的预测长纤维铺层复合材料性能的工具，用于分析复合层合板在设计中可能出现的复杂耦合效应。

下面我们简单走一下整个流程，不求面面俱到。

二、复合材料本构关系

下图中显示的是一个材料积分点在直角坐标系中的应力/应变状态,垂直于作用面的应力/应变分量为正应力/应变,平行于作用面的分量为剪应力/应变。其中六个剪应力/应变满足剪应力/应变互等定理。所以写成张量形式有九项，但是写成向量形式就只有六项。

广义胡克定律反映了各向异性弹性体的应力与应变的线性关系，构成各向异性弹性力学的本构方程。在小变形的情况下，对于弹性体，应变应力关系用广义胡克定律可以表示为：

式中Q表示刚度矩阵。写成柔度矩阵形式如下：

式中S表示柔度矩阵，满足关系式：

可知一般各向异性材料的弹性常数有36个。对于均匀的各向异性体，和均为常数；对于非均匀体它们是坐标的函数。

通过对材料的应变能密度分析得到

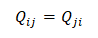
同样可以得到关系式：

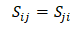
表明刚度矩阵Q和柔度矩阵S都是对称矩阵。由于对称性的存在，各向异性材料的独立弹性常数减少为21个。

三维正交各向异性材料，刚度矩阵弹性常数进一步简化：

求逆得到应变应力关系式：

材料的独立弹性常数减少到九个。可知正交各向异性材料的正应力和剪应变或剪应力和正应变之间没有耦合作用。

如果层合板的厚度比较薄的时候，可用薄翘理论来分析层合板的受力情况。

注意：xyz为材料坐标系，123为某一铺层坐标系。

以下是二维问题柔度矩阵S中的柔度系数定义，

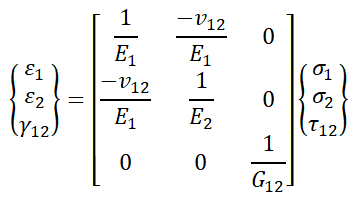
以下是弹性矩阵Q的定义，

刚度矩阵和柔度矩阵关系:

独立的量只有五个：

根据结构对称性可得：

当复合材料主纤维方向与平面坐标系x轴有一夹角𝜃，则需要对刚度矩阵或者柔度矩阵做旋转变换，才能成为该坐标系下的刚度、柔度矩阵

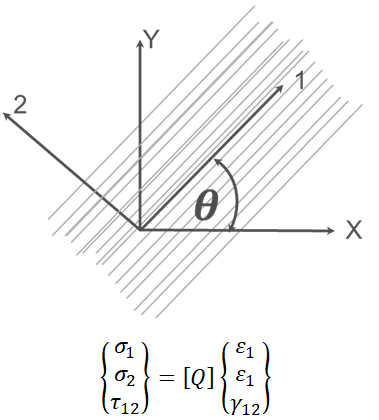
应变矩阵从主纤维方向转换到平面坐标系X轴方向：

其中，

应力矩阵从主纤维方向转换到平面坐标系X轴方向：

其中，

那么，

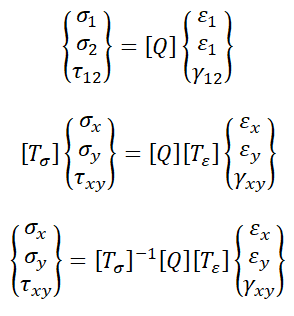
刚度矩阵变换：

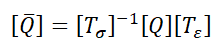
其中，

那么，

柔度矩阵变换，

因此变换后的应力应变关系为：

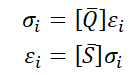
转换后的刚度矩阵展开式：

转换后的柔度矩阵展开式：

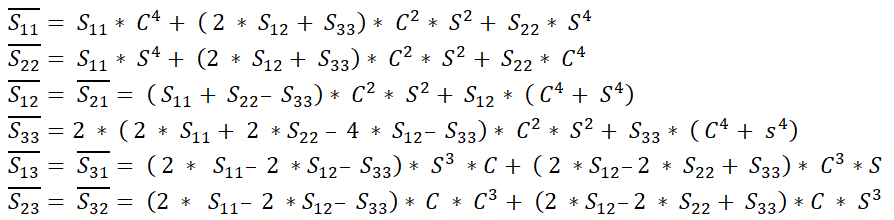
三、经典层合板理论的基本假设

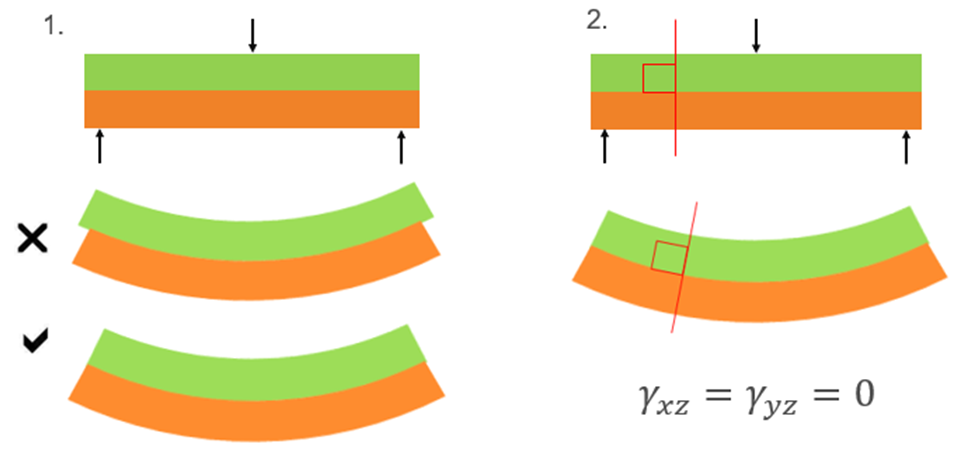
经典层合板理论采用了弹性板壳理论中的直线法假设,在复合材料力学中比较成熟和实用。尽管层合板由多个单层板黏合而成,但由于单层的厚度一般是0.1mm的量级,所以层合板总厚度方向的尺寸与其他两个方向相比要小得多,挠度也远小于厚度,整体上可将层合板视为非匀质的各向异性薄板。

如果有两层或者两层以上的铺层粘结在一起后，可作如下假设(等应变假设)：

• 各单层间黏结牢固,不产生滑移,因而变形在层间是连续的。
• 各层处于平面应力状态。

• 变形前垂直于层板中面的直线段,变形后仍然为垂直变形后中面的直线段,且长度不变。

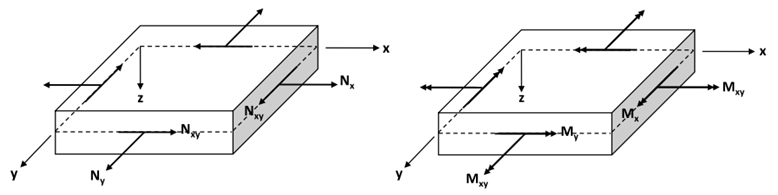
中面载荷

对各向同性材料有：

对于有n个恒定厚度层组成的层压板，中面载荷可以用每个层厚度的应力变化之和表示：

铺层顺序及距离中面位置标定

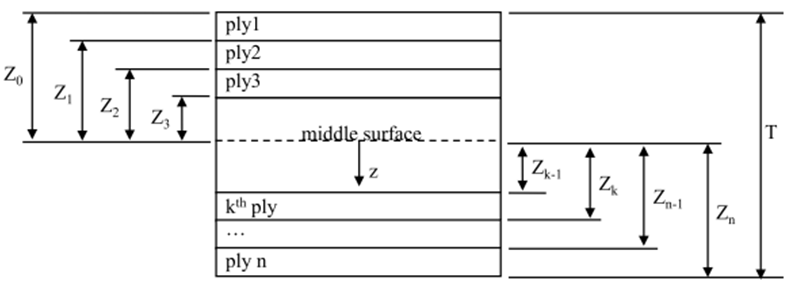
ABD矩阵推导

叠层显示下的面内载荷作用

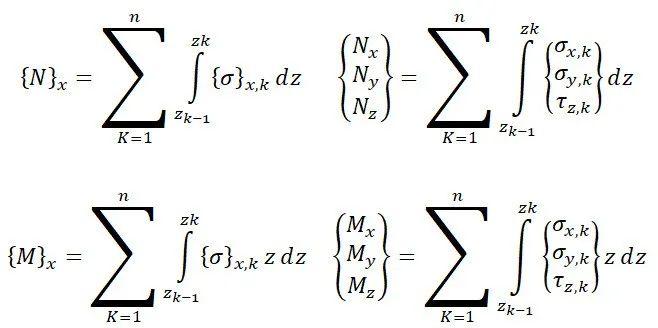
力流 => [A] [B]矩阵

弯矩流 => [B]、[D]矩阵

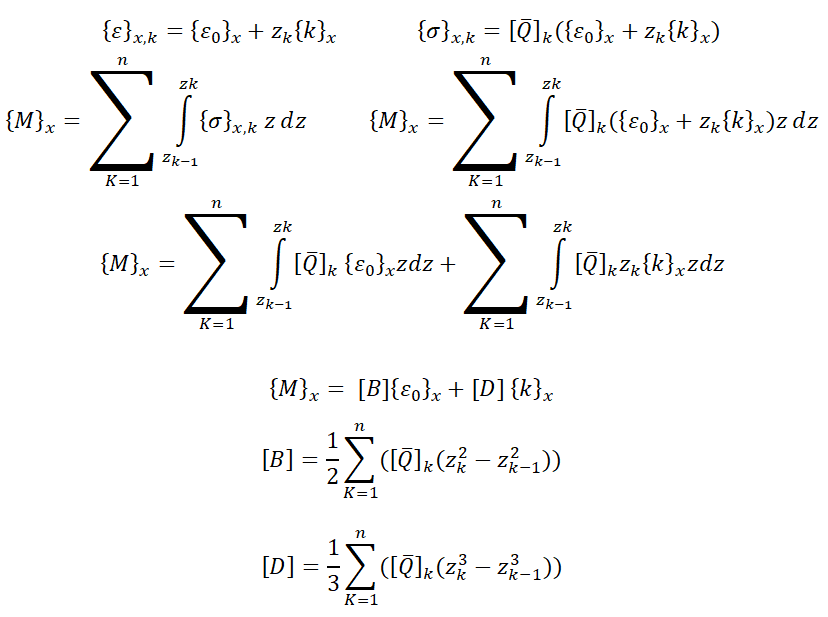
[D]薄板弯曲刚度矩阵

ABD矩阵在设计中的应用

ABD矩阵具体项作用形式

四、专家观点

以下内容摘自余文斌教授《Three Common Mistakes in Mechanics ofComposites》

1、经典层合板理论的内在不一致性（蓝色字体来自原文）

经典板模型的本构关系可以使用以下六个方程来表示：

CLT的传统推导从Kirchhoff假设开始，将3D位移表示为2D板位移，

其中x3是厚度方向，ui是3D位移。3D应变可以用2D板应变和曲率表示为：

εαβ表示三维平面应变。根据Kirchhoff假设平面外应变εi3消失。换句话说，Kirchhoff假设使得层合板为平面应变状态。这与导出方程（20）中的本构关系需要的平面应力假设是相矛盾的。我们知道平面应变与平面应力在大多数情况下不能共存。大多数，如果不是全部的话，学术界对这种明显的矛盾保持沉默。CLT的这种矛盾可以通过结合横向法线的变形来消除，使得

其中wi是描述横向变形的3D波动函数，横向变形在Kirchhoff假设下是无法描述的。等式（23）可以被认为是使用三维波动函数和板位移来描述三维位移长变量变化的方程组。

通过以上文中的内容，我们可以得出目前的主要的矛盾点在CLT中同时使用了平面应力和平面应变假设，而两者一般是不可能同时存在的，但我们目前的教材中对这一点都没有明确的说明。

由于这个矛盾的存在，目前CLT是无法处理层间剪切载荷问题的。如果采用余教授的方法，完全可以使用CLT来得到层间剪切。

目前的大部分商软中使用的基本还是无法得到层间剪切的CLT，余教授的方法已经在SwiftComp软件中得到了具体的实现，大家可以试用。

2、不对称B矩阵（蓝色字体来自原文）

最后一个错误也与CLT有关。在文献中，B矩阵通常是写成：

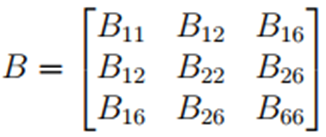
换句话说，在板的本构关系等式（20）中，B矩阵中必须满足B21＝B12，B61＝B16，B62＝B26。对于复合材料层合板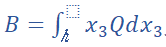，是对称的，因为Q是对称的。但是，不能保证B必须是对称的。事实上，对于一般的复合材料板，如夹芯板使用波纹芯、3D编织复合材料制成的平板或曲板，我们已经发现了B不是对称的情况。那么，最好把本构关系写成等式（20）中那样，考虑B可能不是对称的可能性。去除B矩阵必须是对称性的要求，我们扩大了从CLT导出的经典板模型的应用范围到其他具有任意各向异性的薄板，而不仅仅是复合材料层压板。

如果对以上两个问题感兴趣，请查看原文中的细致分析和描述。

最后用余教授的一句话结束本文，“希望对学界正本清源起到一点作用，错误不至于代代相传。”

五、铺层复合材料建模优化课程

以上就是笔者春节假期总结的HyperMesh铺层复合材料高级建模及优化的经典层合板理论，希望对复合材料建模分析优化学习者有所帮助。为此我的视频教程《铺层复合材料HyperMesh高级建模及OptiStruct仿真优化》也正式上线了。目标是让学习者可以自行进行复合材料建模，仿真及优化设计能力。