搞笑诺贝尔奖:小鸭子为什么在妈妈身后编队游泳?水波动力学中的乘波和破浪行为

摘 要
它们为什么在游泳的时候要保持整齐的编队? 最佳的游泳队形是啥样的? 小鸭子们采用编队游泳的方式,每个个体能节省多少能量?
绪 论

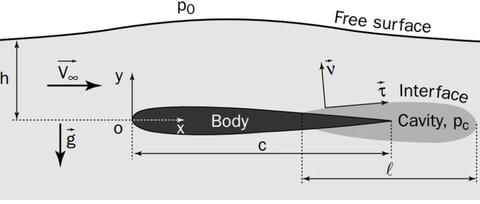
图1(b–d)展示了不同条件下自由水面上一只小鸭子的简化二维力学模型。在图1(b)所示的平静水面条件下,小鸭受到没有水平分量的静水压力。在图1(c)中,小鸭子坐在波浪上,胸部在波峰上,腹部在波谷上。由于波高反映了水面上的压力分布,由于小鸭浸入身体表面的压力积分,预计会产生与运动方向相反的额外阻力。在这种情况下,波浪相互作用的影响是不利于小鸭子向前游泳的,与在平静的水中游泳相比,小鸭子需要为运动付出更多的努力。在图1(d)中,小鸭恰好与图1(c)中所示的波浪呈180°相位差。由于胸部在波谷上,腹部在波峰上,小鸭将被波浪推动,从而减少其移动力。应该注意的是,只有当小鸭与波浪的相对位置保持不变时,从波浪获得的益处才能持续。它要求小鸭的前进速度必须等于波浪的群速度。在编队游泳中,只要后面的小鸭子保持在她们前面游泳的妈妈相同的速度,就可以很容易地满足乘波的条件,因为从固定在前体上的坐标系观察时,前体产生的稳定波不会改变相位。
让我们把定义为一只鸭子或者很多小鸭子在平静的水中单独游泳时的波阻。当它们编队游动时,波阻记为。减阻系数 可定义为。
可定义为。
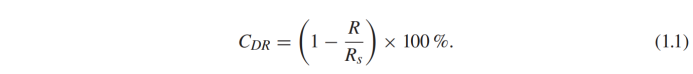
 可用于量化水动力相互作用的强度。
可用于量化水动力相互作用的强度。  >0表示由于水动力的作用,小鸭子游动的波阻减小,而
>0表示由于水动力的作用,小鸭子游动的波阻减小,而  <0表示波阻增加。在
<0表示波阻增加。在  =0时没有发现相互作用,波阻与独立游泳的波阻相同。当
=0时没有发现相互作用,波阻与独立游泳的波阻相同。当  >100%时,此时波阻转化为小鸭子游泳的推进力。显然,小鸭子们都希望获得尽可能大的
>100%时,此时波阻转化为小鸭子游泳的推进力。显然,小鸭子们都希望获得尽可能大的  。
。研究方法与基本假设
穿过自由液面运动的物体的总阻力由两个主要部分组成:波阻和粘性阻力。当速度高于  时(为弗劳德数,可表示为
时(为弗劳德数,可表示为  ,其中U为移动速度,g为重力加速度,L为特征长度),波阻占主导地位(Schultz 2007)。对于人类游泳运动员来说,在水面游泳时,波浪阻力可能占总阻力的60%(文内尔、皮斯和威尔逊,2006年)。对于小鸭子来说,考虑到其较小的体长,弗劳德数通常高于0.25。它们的疏水羽毛可以进一步减少粘性阻力。因此,我们假设波浪阻力是小鸭总阻力的主要组成部分。
,其中U为移动速度,g为重力加速度,L为特征长度),波阻占主导地位(Schultz 2007)。对于人类游泳运动员来说,在水面游泳时,波浪阻力可能占总阻力的60%(文内尔、皮斯和威尔逊,2006年)。对于小鸭子来说,考虑到其较小的体长,弗劳德数通常高于0.25。它们的疏水羽毛可以进一步减少粘性阻力。因此,我们假设波浪阻力是小鸭总阻力的主要组成部分。假设编队游泳的小鸭和以相同速度独立游泳的同一只小鸭之间的粘性阻力差异很小。粘性阻力主要由三个因素决定:游泳速度、浸没体表面的形状和面积。对于以相同速度游泳的同一只小鸭子来说,无论是独立游泳还是编队游泳,这三个因素都可以视为相同。因此,总阻力的差异主要由波阻分量引起。假设波浪阻力减小可用于评估流体动力相互作用的强度。这里不试图分析由流体粘度引起的阻力分量。这一假设与造船工程师在双体船设计中采用的理论一致(Söding 1997;Tuck & Lazauskas 1998)。 假设小鸭子是坚硬光滑的身体。疏水性羽毛和划水足的局部运动将影响总阻力。据推测,这种效应在独立游泳和编队游泳中是一致的。因此,鸭子的几何形状由简单的椭球来模拟。 小鸭子以恒定速度在水面上移动,且小鸭子的俯仰角为零。在我们的计算中既不考虑下沉也不考虑纵倾,因为它们对阻力的影响在低弗劳德数时非常小。 假设水鸟可以本能地找到并停留在阻力最小的位置,而不考虑其他群体成员的运动表现。
结果和讨论
3.1 母鸭后面跟着一只小鸭子(M+1D)
让我们首先调查一下只有一只小鸭跟着母鸭的情况。图2(a)显示了母鸭以0.48m/s的速度移动时产生的波形。波型有两个主要特征:在鸭头和鸭尾部分的每一侧的发散波,以及与鸭子后面的中心线相交的弯曲波峰的横向波。这种波浪模式保持不变,并随着母鸭的身体移动。这个波浪系统的能量是通过做功克服波浪阻力来维持的。图2(a)还显示,大部分波浪能量集中在母鸭尾部波浪系统后面的楔形区域内。
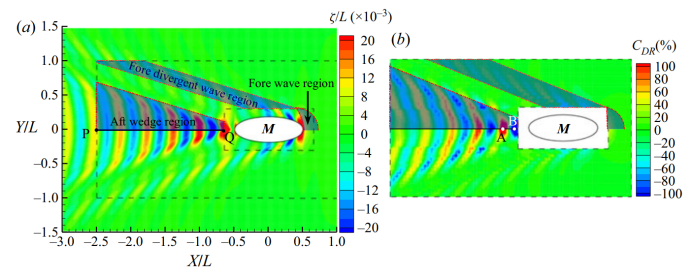 图2.(a)母鸭以U=0.48m/s(Fr=0.244)的速度游泳时的波形。图上的椭圆M代表母鸭(长L=0.4米,宽W=0.15米,深H=0.05米)。云图颜色表示通过其主体长度无量纲化的波高ζ。图中的X和Y横纵坐标是相对于母鸭的坐标,其原点在母鸭的中心。阴影代表母鸭波能量集中的一半区域。PQ线是母鸭后面的中线;
图2.(a)母鸭以U=0.48m/s(Fr=0.244)的速度游泳时的波形。图上的椭圆M代表母鸭(长L=0.4米,宽W=0.15米,深H=0.05米)。云图颜色表示通过其主体长度无量纲化的波高ζ。图中的X和Y横纵坐标是相对于母鸭的坐标,其原点在母鸭的中心。阴影代表母鸭波能量集中的一半区域。PQ线是母鸭后面的中线;
(b)当小鸭子(长l=0.1米,宽w=0.05米,深h=0.017米)在图(a)中两个黑色虚线框之间的区域以相同的速度跟随母鸭游动时,其阻力减小系数的分布。阴影代表主要流体动力相互作用发生的一半区域。
现在,把一只小鸭子放入图2(a)所示的靠近母鸭的内部和远离母鸭的外部之间的区域,让它以与母鸭相同的速度游泳。我们计算了该区域1290个位置(半个计算域)的波阻,并获得了一个减阻轮廓,如图2(b)所示。可以观察到母鸭的波形和小鸭的 轮廓之间有很高的一致性。图2(b)中有三个主要的
轮廓之间有很高的一致性。图2(b)中有三个主要的 密集区域,对应于图2(a)中的三个波能量集中区域。最强烈的水动力相互作用发生在波能集中的尾部楔形区域。最大和最小
密集区域,对应于图2(a)中的三个波能量集中区域。最强烈的水动力相互作用发生在波能集中的尾部楔形区域。最大和最小 (位置A和B)出现在母鸭后面的中心线上。假设小鸭已经对阻力产生了本能的感觉,它将保持在位置A以获得最小的阻力。此外,当小鸭在母鸭后面游泳时,没有横向力和偏航力矩作用在小鸭上,因为小鸭遇到的水流关于中心线对称。因此,只要小鸭子保持与母鸭相同的速度,它就可以毫不费力地达到稳定的乘波状态,从而节约其能量消耗。
(位置A和B)出现在母鸭后面的中心线上。假设小鸭已经对阻力产生了本能的感觉,它将保持在位置A以获得最小的阻力。此外,当小鸭在母鸭后面游泳时,没有横向力和偏航力矩作用在小鸭上,因为小鸭遇到的水流关于中心线对称。因此,只要小鸭子保持与母鸭相同的速度,它就可以毫不费力地达到稳定的乘波状态,从而节约其能量消耗。
小鸭子的另一个选择是在母鸭前面游泳(在母鸭的fore波上)。从图2(a)可以看出,该区域有一个波峰,该波峰在上游迅速消失。因此,当小鸭在该区域游泳时,它将持续乘波,并且该区域的水波作用力始终为动力而非阻力(如图2b所示)。这表明母鸭可以推动小鸭子游到她前面。当小鸭在母鸭前面的中心线游泳时,也没有横向力和偏航力矩作用在小鸭上。然而,副作用是显而易见的。不考虑社会行为(例如抵御捕食者),潜在利用的波浪能相对较小。当小鸭子非常靠近妈妈的前胸时,它只会受益于一个小的“推力”。随着小鸭向更上游的地方移动,这种好处很快就消失了。因此,如果一个编队中有不止一只小鸭,其他成员很难获得任何帮助它们移动的好处。
当小鸭在母鸭前发散波的两侧游泳时,也观察到了水动力相互作用。然而,这些区域对小鸭的吸引力较小,因为相互作用力较小。此外,母鸭产生的波浪会破坏小鸭流场的双边对称性,因此产生横向力和偏航力矩。为了跟随母亲,小鸭子不得不花更多的力气来保持它的路线和航向角。
从图2可以得出结论,小鸭子最有可能在妈妈身后的中线游泳。现在,将小鸭放在中心线上,并逐渐将其位置从P改为Q(如图2a所示)。图3显示了小鸭子和母鸭的波浪阻力减小情况以及波浪模式。从图3的结果中有三个主要发现。
根据与母鸭的相对位置,尾随小鸭跟随母鸭尾流经历阻力增加( <0)和阻力减小(
<0)和阻力减小( >0)的概率相等,如图3(a)中的蓝色实线所示。小鸭的
>0)的概率相等,如图3(a)中的蓝色实线所示。小鸭的 曲线呈现周期性,在一个中性值附近波动。随着小鸭向下游游得更远,摆动幅度逐渐减弱。衰减率与传播到下游远场的波的衰减率非常匹配。
曲线呈现周期性,在一个中性值附近波动。随着小鸭向下游游得更远,摆动幅度逐渐减弱。衰减率与传播到下游远场的波的衰减率非常匹配。 曲线上两个连续波峰之间的距离(d)与波长(λ)完全相同。由于移动物体后中心线上的波长与速度有关
曲线上两个连续波峰之间的距离(d)与波长(λ)完全相同。由于移动物体后中心线上的波长与速度有关  ,只要小鸭保持与母亲相同的速度,它就总能以较小的游泳力将自己调整到一系列位置。我们将虚拟小鸭放置在对应于
,只要小鸭保持与母亲相同的速度,它就总能以较小的游泳力将自己调整到一系列位置。我们将虚拟小鸭放置在对应于 曲线每个波峰的位置。可以观察到这些都是乘波的位置(小鸭的胸部在波谷上,腹部在波峰上),这与图1(d)所示的简化二维模型的预测一致。在
曲线每个波峰的位置。可以观察到这些都是乘波的位置(小鸭的胸部在波谷上,腹部在波峰上),这与图1(d)所示的简化二维模型的预测一致。在 曲线的第一个波峰处发现最大 波阻降低158%,这表明小鸭在位置A处的总波阻为正(100%用于克服其自身的波阻,而其余58%转化为推力,驱动小鸭前进)。在多艘船的水箱试验中也观察到了正阻力(指向移动方向的阻力)(Vantorre、Verzhbitskaya和Laforce,2002年)。铁人三项游泳的实验数据也证实了这一点(Bassett等 1991;Janssen, Wilson & Toussaint 2009)认为,跟随者越接近领导者,其获得的辅助减阻效果就越好。随着鸭妈妈到小鸭距离的增加,曲线的幅度会减小。在第5个波峰时,小鸭子距离妈妈2.4L(母鸭划水加速的水流可能会分散),小鸭子仍然可以获得高达87%的波浪减阻效果。但同样也存在一些阻力增加的区域。特别是,在位置B处观察到减阻系数变为了-187%,此时小鸭非常接近地跟随其母亲。这与图1(c)所示的简化二维模型推断的坐浪位置相似。这种阻力增加的现象是通过对人类游泳者被动阻力的实验测量观察到的(让桑等人,2009年)。然而,在Fish对小鸭的实验中没有观察到这种现象(Fish 1994)。一个可能的原因是,小鸭子凭本能决定它们的位置,确保它们只在阻力减小的区域游泳。
曲线的第一个波峰处发现最大 波阻降低158%,这表明小鸭在位置A处的总波阻为正(100%用于克服其自身的波阻,而其余58%转化为推力,驱动小鸭前进)。在多艘船的水箱试验中也观察到了正阻力(指向移动方向的阻力)(Vantorre、Verzhbitskaya和Laforce,2002年)。铁人三项游泳的实验数据也证实了这一点(Bassett等 1991;Janssen, Wilson & Toussaint 2009)认为,跟随者越接近领导者,其获得的辅助减阻效果就越好。随着鸭妈妈到小鸭距离的增加,曲线的幅度会减小。在第5个波峰时,小鸭子距离妈妈2.4L(母鸭划水加速的水流可能会分散),小鸭子仍然可以获得高达87%的波浪减阻效果。但同样也存在一些阻力增加的区域。特别是,在位置B处观察到减阻系数变为了-187%,此时小鸭非常接近地跟随其母亲。这与图1(c)所示的简化二维模型推断的坐浪位置相似。这种阻力增加的现象是通过对人类游泳者被动阻力的实验测量观察到的(让桑等人,2009年)。然而,在Fish对小鸭的实验中没有观察到这种现象(Fish 1994)。一个可能的原因是,小鸭子凭本能决定它们的位置,确保它们只在阻力减小的区域游泳。
尾随小鸭在领头鸭的尾流中游泳时受到强烈的流体动力相互作用并不奇怪。然而,母鸭是否会因为尾随小鸭的存在而受到阻力的减小,从而在编队游泳中实现互利?关于公路自行车运动的实验研究(Blocken等,2013)证实了这种跟随运动方面的互利性,但从未有关于鸭子的报告。我们的计算提供了证据来支持这一假设,即紧跟在领头鸭后面游泳的尾随小鸭也会帮助领头鸭。从图3(a)中的蓝色虚线曲线可以看出,当小鸭直接在母鸭身后游泳时,母鸭的波阻可以减少35%。由于小鸭的前浪,分布在母鸭后部的压力增加了。结果,母鸭乘着小鸭子的船头浪而受益。然而,在这个位置上,小鸭是失败者。它的波浪阻力减少了116%,这表明与独自游泳时相比,小鸭必须花费两倍以上的努力来克服波浪阻力。当小鸭在位置A游泳时,观察到双赢的情况,母鸭节省了5%,小鸭节省了158%的波浪阻力。随着分离的增加,小鸭子给母鸭的艏波减阻的利好迅速减少。对母鸭几乎没有交互影响,因为间隔变得比小鸭的体长还大。
我们还发现小鸭在A位置游泳时节省能量,而在b位置消耗更多能量。图3(b)和3(c)中的波形解释了出现这种现象的原因。当小鸭在位置A乘波时,观察到减阻的波浪干扰现象,如图3(b)所示。波浪抵消主要发生在母鸭的尾部楔形区域,这与图2(b)所示的波浪阻力减小一致。尾随小鸭产生的波的相位与母鸭产生的波的相位不同。通过叠加,下游波被部分抵消。把母鸭和小鸭子作为一个整体系统(M+1D),它需要系统做更少的工作来维持合成波能。由于波浪被限制在开尔文楔形区的下游,母鸭只能从波浪抵消中获得非常有限的好处。尾随小鸭得到的主要好处是减少了其运动的阻力。比较图3(b)和2(a)中的波浪模式,我们还可以发现M+1D产生的波浪甚至不如单只母鸭产生的波浪强烈。它解释了为什么当小鸭在位置A游泳时,作用在小鸭上的波浪阻力变为推力(
 >100%)。相反,当小鸭在位置B的波浪上游泳时,观察到增阻的波浪干扰。由于开尔文波的下游传播特性,放大 波携带的额外能量主要从小鸭的能量消耗中提取。如图3(a)所示,这与阻力在位置B增加的事实相吻合。
>100%)。相反,当小鸭在位置B的波浪上游泳时,观察到增阻的波浪干扰。由于开尔文波的下游传播特性,放大 波携带的额外能量主要从小鸭的能量消耗中提取。如图3(a)所示,这与阻力在位置B增加的事实相吻合。

图3.(a)波浪阻力减小随小鸭子和鸭妈妈之间距离的变化。蓝色实线上的点A和B对应于图2(B)中的相同点,代表最大和最小波浪减阻位置。这里d是 曲线上两个连续峰值之间的距离。红色实线是母鸭后中心线上的波浪轮廓,λ是波长。图(b)和(c)中的椭圆D代表小鸭。
曲线上两个连续峰值之间的距离。红色实线是母鸭后中心线上的波浪轮廓,λ是波长。图(b)和(c)中的椭圆D代表小鸭。
(b)当小鸭在位置a游泳时的波形图;
(c)当小鸭在位置b游泳时的波形图。
它们会在每个  波峰处定位,以便形成图3(a)所示的单行吗?
波峰处定位,以便形成图3(a)所示的单行吗?编队中的每个个体可以节省多少波阻?
 =158%)。M+D1系统后面的剩余波浪能仍然足以使D2获得推进力(
=158%)。M+D1系统后面的剩余波浪能仍然足以使D2获得推进力(  =132%,其中100%用于克服其波浪阻力,剩余的32%转化为推进力)。D3利用的波浪能进一步减少。最终,D3后面的小鸭子实现了波浪阻力减小的稳定状态。波阻降低保持在大约100%,这表明D3后面的所有小鸭子都获得了相同量的辅助来平衡它们的波阻。由于Dn(n>3)上的波浪阻力为零,这些小鸭获得了自由航行的环境,并且没有做任何工作来产生额外的波浪能。这些小鸭子的作用是维持海浪并将它们传递给后面的小鸭子。我们称这种微妙的平衡状态为波传递。在图4(a)所示的波型以及图4(b)所示的波形中也可以观察到这种波传递现象。D3后面的波经过D4,然后相同的波保持在D4后面。重复这个过程,从母鸭发出的波能量最终将到达第n只小鸭,而不管是否分离。将M+nD作为一个整体系统,M+3D的总波阻最小。随着拖尾小鸭数量的增加,总波浪阻力将保持在这一最低水平。应该注意的是,波的传播是在固定于物体上的运动坐标系下建立的一种微妙的动态平衡。只有当个体保持与母鸭相同的速度,并按顺序停留在母鸭后面中心线上的正确位置时,才能实现这一目标。任何不遵守秩序的个体都将破坏复杂的平衡。
=132%,其中100%用于克服其波浪阻力,剩余的32%转化为推进力)。D3利用的波浪能进一步减少。最终,D3后面的小鸭子实现了波浪阻力减小的稳定状态。波阻降低保持在大约100%,这表明D3后面的所有小鸭子都获得了相同量的辅助来平衡它们的波阻。由于Dn(n>3)上的波浪阻力为零,这些小鸭获得了自由航行的环境,并且没有做任何工作来产生额外的波浪能。这些小鸭子的作用是维持海浪并将它们传递给后面的小鸭子。我们称这种微妙的平衡状态为波传递。在图4(a)所示的波型以及图4(b)所示的波形中也可以观察到这种波传递现象。D3后面的波经过D4,然后相同的波保持在D4后面。重复这个过程,从母鸭发出的波能量最终将到达第n只小鸭,而不管是否分离。将M+nD作为一个整体系统,M+3D的总波阻最小。随着拖尾小鸭数量的增加,总波浪阻力将保持在这一最低水平。应该注意的是,波的传播是在固定于物体上的运动坐标系下建立的一种微妙的动态平衡。只有当个体保持与母鸭相同的速度,并按顺序停留在母鸭后面中心线上的正确位置时,才能实现这一目标。任何不遵守秩序的个体都将破坏复杂的平衡。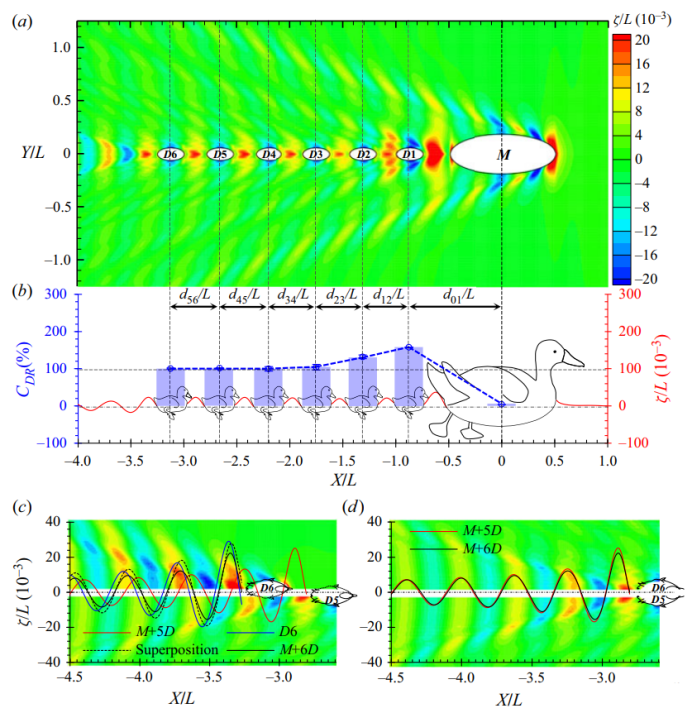
 是两个相邻个体之间的间隔,其中下标n=0表示母鸭。虚拟小鸭子被放在波阻最小的位置。图(b)中的误差条显示了数值离散化引起的误差。图片(c)和(d)显示了波型和波形的分解。
是两个相邻个体之间的间隔,其中下标n=0表示母鸭。虚拟小鸭子被放在波阻最小的位置。图(b)中的误差条显示了数值离散化引起的误差。图片(c)和(d)显示了波型和波形的分解。 的M+6D的波形。将图(c)中的黑色实线向上游移动
的M+6D的波形。将图(c)中的黑色实线向上游移动  ,我们可以获得图(d)中的黑色曲线。
,我们可以获得图(d)中的黑色曲线。波浪通过解释了为什么在鸭子和人类在公开水域游泳比赛中经常能观察到单列队形,对这一现象的研究让我们更深入地研究波传递的最基本原理。在这里,我们选择D6作为典型的波浪传递者,它遇到来自D5的波浪,然后向下游传递相同的波浪。分解波形和波形有助于我们分析理解这一现象。我们先假设D6不存在,则其是一个最优的M+5D结构,我们可以得到一个波形图(如图4c的下半部分轮廓所示),以及D5后面的波形轮廓(如图4c中的红色实线所示)。现在,让一只小鸭子在D6的位置独立游泳。图4(c)的上半部分轮廓和蓝色实线分别显示了其波形和轮廓。根据对M+1D编队的讨论,出现了波浪抵消,并且由M+5D和D6产生的波浪被部分抵消,从而导致阻力减小。然而,图4(c)中的结果表明这两个波系统不是异相的。它们之间的相位角非常微妙,以至于在D6之后可以获得与M+5D振幅几乎相同的合成波形。让我们将M+5D的波剖面向上游移动的相位,这是d5和D6之间的无量纲分离。如图4(d)所示,我们可以看到M+5D和M+6D后面的波形轮廓非常一致,这表明D6成功地维持并越过了波浪。
我们的研究表明,小鸭应用乘波和破浪原理来减少波浪阻力,从而改善它们的运动性能。它们最有可能排成一列纵队游泳,这样每个小鸭子都能得到总体最大化的助力。波浪通过伴随着动态平衡,在这种平衡下,无论群体大小如何,群体的总波阻都保持不变。这些原则有可能应用于设计现代货运船,以在不增加燃料成本的情况下运输更多货物。
在水面上编队移动时获得的利好也可能影响小鸭子的原始本能,驱使小鸭子下意识地跟随它们在岸上一段时间内看到的任何移动物体,因为它们对印迹更敏感。虽然印迹的机制还没有完全被理解,但这项研究揭示了流体力学对动物行为和潜在进化的重要性。