数学物理方程理论基础
文章摘要
文章介绍了梯度、散度和旋度的概念及意义。梯度是一个向量,指示函数在某点变化最快、变化率最大的方向。沿着梯度方向,函数值增大;反之减小;垂直于梯度方向,函数值不变。散度是通量的强度,表示场的有源性,散度为正表示有通量产生,为负则表示吸收通量。旋度表示环流量的强度,通过右手定则判断其方向。文章最后汇总了散度、梯度和旋度的基本公式。
正文

梯度
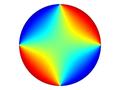
在空间中的每一个点都可以确定无数个方向,一个多元函数在某个点也必然有无限多个方向。因此,导数在这无限多个方向导数中最大的一个(最大的导数直接反映了此函数在该点变化率的数量级)等于多少?它是沿哪个方向达到的?描述这个最大方向导数及其所沿方向的矢量,便是梯度。
梯度的本意是一个向量(矢量), 表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。任何场都可以用来理解梯度,后来被引用到数学中用来指明函数在指定点的变量率最快的方向和大小,是一种变化效率的数字抽象。
梯度的定义为:

在数学上可以改写为:

根据梯度的定义可知:
(1)沿着梯度方向走,函数值增大;
(2)沿着相反于梯度的方向走,函数值减小
(3)垂直于梯度方向,函数值不变
散度
理解散度之前,必须理解通量。通量简言之,单位时间内通过某个曲面的量。对于曲面,其通量为:

散度:向量场A中M点的散度可以表示为:

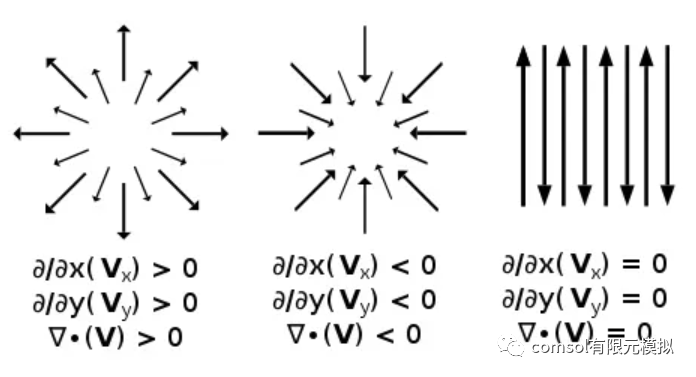
就是闭合曲面围成空间中的通量除以围成空间体积,然后令曲面无限小,此时计算出来的就是散度。
散度是通量的强度,其物理意义表示场的有源性。如果散度为正,表明向量场在这一点或这一无限小的区域有通量产生,表明该处有水流的涌出,即有源性。如果散度为负,表明此处没有新的通量产生,且会吸收水流。
旋度
类似于通量,我们也可以把各个点环流量的强度加起来,得到环流量。而通过不断缩小封闭区域就可以得到环流量的强度,即旋度。

此时M点旋度可以表示为:

当然,旋度还有方向。其方向通过右手定则进行判断。大拇指所指方向为旋度的方向,知道大拇指的方向就知道封闭曲线呈顺时针还是逆时针旋转了。
散度-梯度-旋度基本公式汇总