机器学习与力学控制:智能颗粒、裂纹反演、本构关系
本文摘要(由AI生成):
本文综述了复杂流动中智能颗粒游动策略的研究进展,包括强化学习原理、深度学习网络结构、缺陷识别、裂纹、人工神经网络、网格生成、背景网格法、径向基函数、有向图表示的本构关系、AlphaGo Zero实现的自主学习过程、三轴数值试样、滚筒内的颗粒分布、切向速度与实验数据的比较等方面的内容。
文一:

doi:10.6052/0459-1879-21-402
复杂流动中的智能颗粒游动策略研究进展
摘要:
智能颗粒定义为可以根据环境的变化而主动调整自身在流场中运动的颗粒,一般用于描述微小的游动物体,如微生物、浮游生物和微纳机器人。由于颗粒运动学特性和流场环境的复杂性,探索智能颗粒的运动策略是一项具有现实意义与挑战性的研究。近期强化学习算法被应用于智能颗粒的运动策略研究,并取得一定进展。本文将讨论强化学习在智能颗粒研究中的应用,并介绍浮游生物运动策略的相关研究进展,包括适用于海洋浮游生物的游动颗粒模型,以及强化学习的基本原理和此类问题的研究框架。海洋浮游生物的昼夜垂直迁移对其生存和繁衍至关重要,生物学研究表明某些浮游生物可感知周围的流场信息,但能否利用这些信息提高垂直方向游动效率仍是一个未知的问题。基于这一背景,相关研究考虑了重力沉降和颗粒形状对浮游生物垂直游动策略的影响。研究发现细长的颗粒能够更加高效地垂直向上运动,而重力沉降则导致智能游动策略发生较大变化。在此基础上,后续研究进一步考虑了局部流体信号的作用,并讨论了基于局部信息在全局坐标系中定向运动的可能性。当颗粒只能感受到局部流体信号时,必须破坏动力学系统的对称性,否则颗粒无法学到有效的垂向游动策略。此外,研究还发现强化学习能够利用流体信号背后的机制,得到颗粒在二维定常流动和三维非定常湍流中高效垂直运动的策略。这些智能游动策略依赖于本质的物理规律,因此这些策略在更加复杂或真实的流动中也可能有优秀的表现。
关键词:
智能颗粒,强化学习,浮游生物,垂直迁移

图:(a)智能颗粒示意图。x-y-z为全局坐标系,n-p-q为颗粒局部坐标系。(b)强化学习原理示意图

图:智能颗粒垂直运动速度随形状和重力沉降作用的变化。颗粒速度以流动的特征速度无量纲化。RL:强化学习得到的智能策略,naive:简单策略,settle:考虑沉降作用

图:(a)智能颗粒在二维Taylor-Green旋涡流动中的运动轨迹。红点表示颗粒的初始位置,背景为涡量云图。(b)智能颗粒与非智能颗粒当地流体垂直方向速度4,的概率密度分布(PDF)
文二:

doi:10.6052/0459-1879-21-360
基于SBFEM和深度学习的裂纹状缺陷反演模型
摘要:
结构内部缺陷的识别是结构健康监测的重要研究内容,而当前以无损检测为主的结构安全检测多以定性分析为主,定量识别缺陷的尺度较困难。本文将比例边界有限元法(scaled boundary finite element methods,SBFEM)和深度学习相结合,提出了基于Lamb波在结构中传播时的反馈信号定量识别结构内部裂纹状缺陷的反演模型。通过随机生成缺陷信息(位置、大小),采用SBFEM模拟Lmb波在含不同缺陷信息的结构中的信号传播过程,SBFEM仅需对结构边界离散可最小化网格重划分过程,大大提高了计算效率。Lmb波在含裂纹状缺陷结构中传播时观测点的反馈信号包含大量的裂纹信息,基于这一特性可为深度学习模型提供足够多的反映问题特性的训练数据。建议的缺陷反演模型规避了传统反分析问题的目标函数极小化迭代过程,在保证计算精度的前提下大大减少了计算成本。对含单裂纹和多裂纹板的数值算例进行分析,结果表明:建立的缺陷识别模型能够准确地量化结构内部的缺陷,对浅表裂纹亦有很好的识别效果,且对于含噪信号模型仍具有较好的鲁棒性。
关键词:
无损检测,比例边界有限元法,深度学习,反分析问题,缺陷识别,裂纹
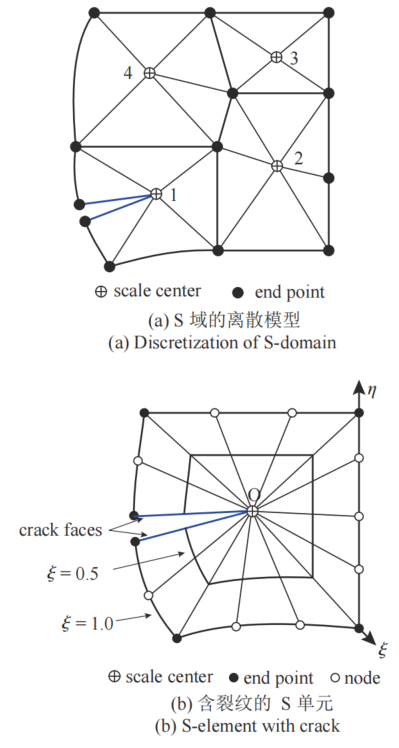
图:比例边界有限元S域和S单元示意图
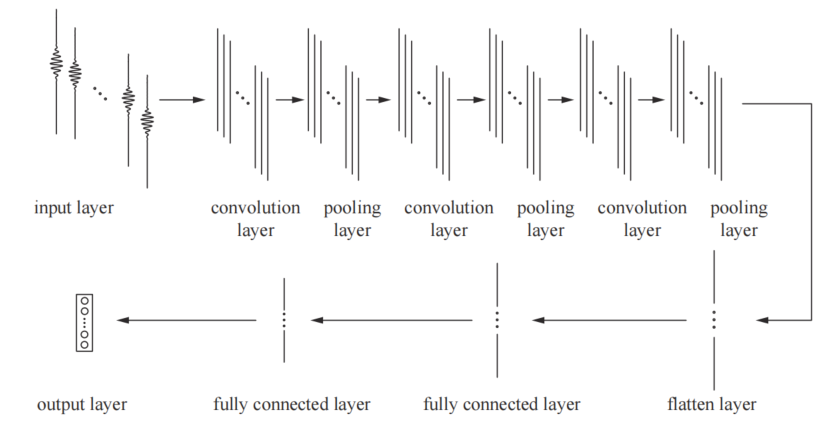
图:深度学习网络结构图
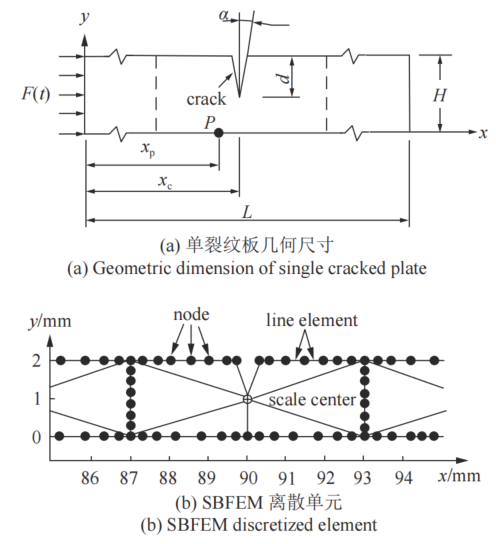
图:单缺陷板几何尺寸及SBFEM边界离散

图:多裂纹测试集反演结果图(续)
文三:

doi:10.6052/0459-1879-21-334
基于人工神经网络的非结构网格尺度控制方法
摘要:
网格自动化生成和自适应是制约计算流体力学发展的瓶颈问题之一,网格生成质量、效率、灵活性、自动化程度和鲁棒性是非结构网格生成的关键问题。在非结构网格生成中,网格空间尺度分布控制至关重要,直接影响网格生成质量、效率和求解精度。采用传统的背景网格法进行空间尺度分布控制需要在背景网格上求解微分方程得到背景网格上的尺度分布,再将网格尺度从背景网格插值到真实空间点,过程十分繁琐且耗时本文从效率和自动化角度提出两种网格尺度控制方法,首先发展了基于径向基函数(RBF)插值的网格尺度控制方法,通过贪婪算法实现边界参考点序列的精简,提高了RBF插值的效率同时,还采用人工神经网络进行网格尺度控制,初步引入相对壁面距离和相对网格尺度作为神经网络输入输出参数,建立人工神经网络训练模型,采用商业软件生成二维圆柱和二维翼型非结构三角形网格作为训练样本,通过训练和学习建立起相对壁面距离和相对网格尺度的神经网络关系。进一步实现了二维圆柱、不同的二维翼型的尺度预测,RBF方法和神经网络方法的效率与传统背景网格法相比提高了5~10倍,有助于提高网格生成的效率。最后,将方法推广应用于各向异性混合网格尺度预测,得到的网格质量满足要求。
关键词:
人工神经网络,网格生成,网格尺度,背景网格法,径向基函数
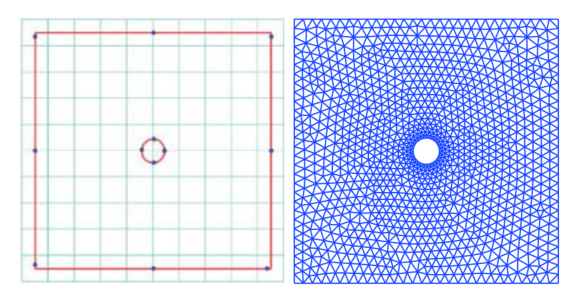
图:圆柱算例点源设置及网格生成情况

图:RBF网格变形方法

图:ANN模型各向同性网格预测结果
文四:

doi:10.6052/0459-1879-21-312
基于深度强化学习算法的颗粒材料应力-应变关系数据驱动模拟研究
摘要:
颗粒材料的宏观力学行为受颗粒组分等材料参数,孔隙率、配位数等状态参数的影响,同时又具备复杂的加载路径和加载历史相关性,建立包含多个内变量以及各变量间相互关联的颗粒材料本构模型是一个重要的科学难题。不同于传统的基于屈服面、流动法则和硬化函数框架下的唯象本构模型,本文基于颗粒物质力学的研究基础,以颗粒材料平均孔隙率、细观组构参数和弹性刚度参数作为内变量,结合深度学习方法建立以有向图表征的数据本构模型。有向图中以不同的链接网络表示不同的内变量信息流动方向,各个内变量间的映射关系采用循环神经网络来建立,将各个神经网络相互组合,形成包含不同内变量且具有不同预测能力的本构模型。该本构模型的建立过程等价于在众多可能的内变量链接关系空间中寻找最能描述实际材料宏观应力应变行为的优化问题。因此,可将有向图本构模型的建立过程看作“马尔可夫决策过程,采用深度强化学习算法构建有向图的内变量链接组合优化过程,具体采用AlphaGo Zero算法自动寻找最优的颗粒材料数据驱动本构模型建模路径。研究结果表明,采用有向图和深度强化学习算法可建立起完全依靠“数据驱动”的颗粒材料应力一应变关系。此外,本方法提供了一种将不同理论模型从数据角度统一起来,且基于人工智能算法发展更优模型的研究思路,可为相似问题的研究提供借鉴。
关键词:
颗粒材料,应力-应变关系,离散元法,深度强化学习,有向图
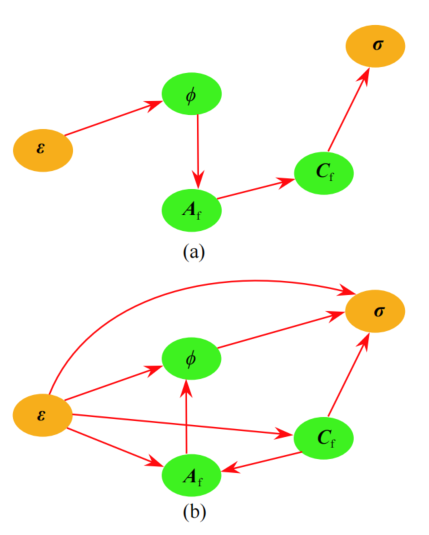
图:有向图表示的两种本构关系

图:一次完整的有向图本构关系建立过程
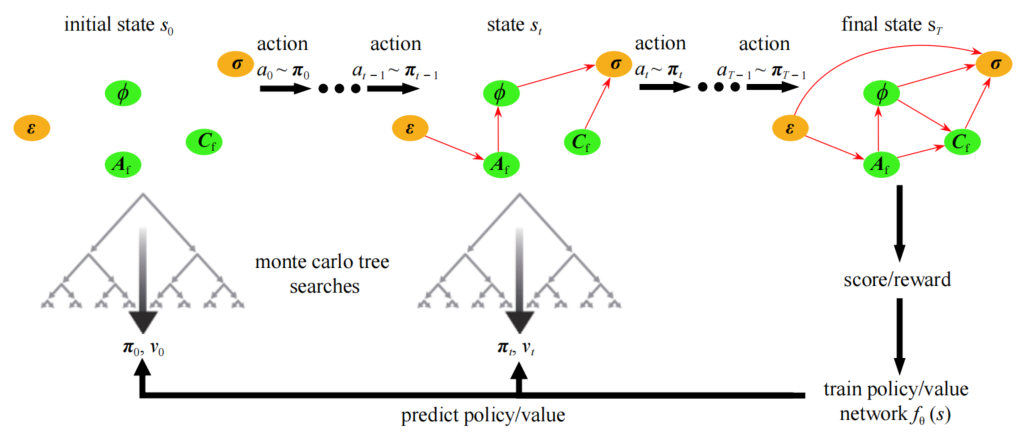
图:AlphaGo Zero实现的自主学习过程

图:三轴数值试样
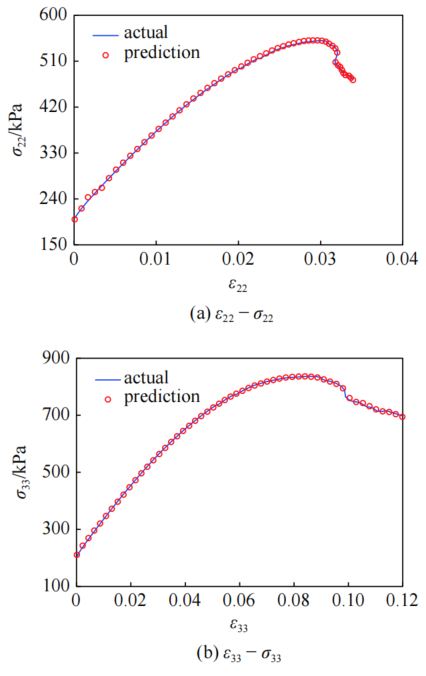
图:等b加载下“数据”本构模型预测比较
文五:

doi:10.6052/0459-1879-21-313
基于离散单元法和人工神经网络的近壁颗粒动力学特征研究
摘要:
颗粒与壁面的相互作用往往对颗粒流动具有显著影响。为研究颗粒与壁面作用机理,对滚筒内颗粒流动过程进行离散单元法(DE)数值模拟。基于模拟结果统计分析靠近壁面处颗粒的运动特征,结果表明,小摩擦系数时颗粒平动和旋转速度均近似满足正态分布,但由于壁面影响,摩擦系数增大时颗粒沿滚筒轴向的旋转速度偏离正态分布,颗粒动力学理论推导壁面边界条件时应考虑速度正态分布的修正及速度脉动的各向异性。采用人工神经网络(ANN)构建了颗粒无因次旋转温度、滑移速度和平动温度之间的函数模型,进而可以在常规双流模型壁面边界条件中考虑颗粒旋转的影响。基于DEM模拟及结果分析可以为壁面边界条件的理论构造和半经验修正提供基础数据和封闭模型。

图:滚筒内的颗粒分布

图:切向速度与实验数据的比较
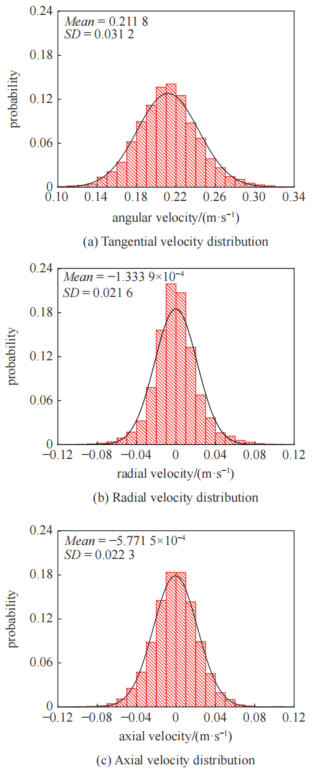
图:近壁颗粒平动速度分布
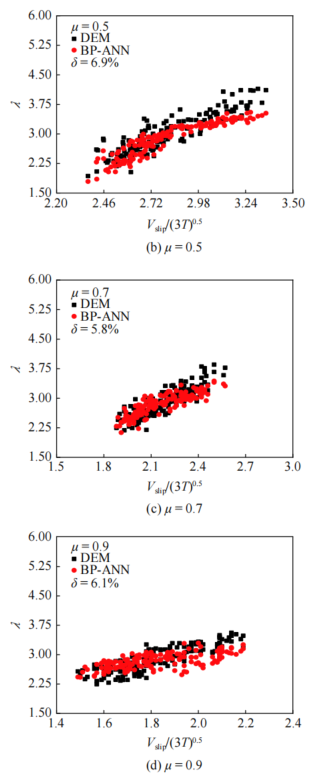
图:无因次旋转温度的模型预测与DEM统计结果对比




