STAR-CCM+求解算法
本文摘要(由AI生成):
这篇文章主要讨论了如何提高 STAR-CCM+软件的整体性能,特别是在考虑湍流求解器的隐式/显式收敛性平衡时,通过调整相关参数来提高收敛速度和稳定性。文章以机翼为例,探讨了如何平衡 Courant 数和显式松弛来实现更快的收敛速度,并介绍了一些高级技巧,如网格序列(GSI)和专家驱动程序(ED),以及如何调整湍流模型的参数以提高收敛性。文章还提出了一些建议,如在外部空气动力学的不同流动区域中使用 GSI+ED(隐式求解器和显式离散化),并根据具体情况调整 CFL 数和 ω(e)值等相关参数。同时,在某些情况下可以考虑添加连续性收敛加速器(CCA)以加快收敛速度。但需要注意,每个具体的案例可能会有不同的最佳参数设置,需要根据具体问题进行调整。
STAR-CCM+提供了两种主要的流动求解器,耦合求解器和分离求解器;耦合求解器对于所有航天外部流动应用来说是推荐的,其同时求解连续性、动量和能量守恒方程,但内存需求较高,具有强大的求解加速技术。分离求解器适用于低速流动(弱或无可压缩性), 使用SIMPLE算法,压力修正方程具有椭圆特性,在保持质量守恒性质方面表现良好,粗略地说,使用分离求解器计算收敛相对于求解器不敏感的案例。
耦合求解器具有许多工具来优化收敛速度和稳定性,这些工具帮助简化用户的设置过程,但了解每个参数如何影响求解器仍然很重要。耦合求解器关键的参数包括:Courant数,显式松弛,无粘性通量。Courant数确定求解器的局部伪时间步长,是线性系统隐式松弛的一种形式,帮助确定解决方案的“delta”向量,低值有助于提高稳定性,高值有助于提高速度。显式松弛决定要使用多少“delta”向量,合适的值有助于避免振荡,正确使用可以同时提高稳定性和速度。无粘性通量控制所需的耗散,“Roe FDS”(默认)推荐用于亚音速和跨音速流动,“AUSM+ up” 推荐用于超音速和高超音速。
以机翼为例,说明耦合求解器两个主要参数之间的相互作用:Courant数和显式松弛。案例细节为2D机翼,高升力构型,Ma=0.2; Re=9M。
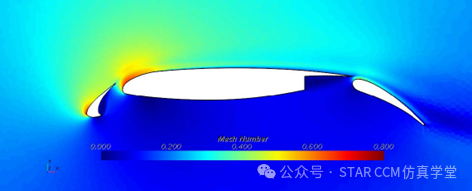
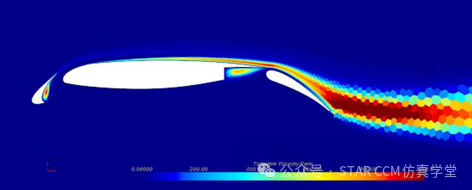
求解设置为CFL=25,𝜔ex=1.0,CFL数在1到100次迭代线性增加,收敛分为4个阶段。
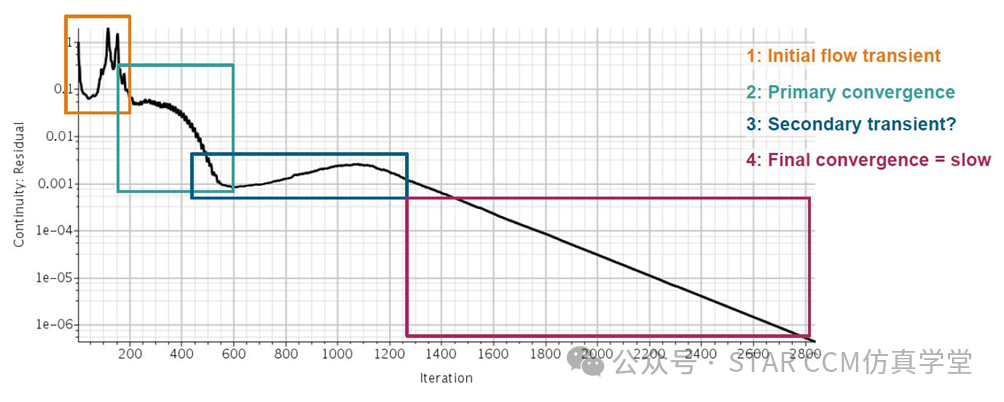
如果我们只增加Courant数(CFL数),而不改变显式松弛,则最初的收敛速度可能会更快,但后面可能会导致不稳定和发散,这在图中用黑色虚线表示。另一方面,如果我们减小显式松弛而不改变Courant数,则整体收敛速度可能会变慢,如图中红色实线所示,但在迭代过程中可以提供更好的稳定性。那么,如果我们同时增加Courant数并减小显式松弛,在这种情况下,我们可以实现更快的收敛速度,如图中红色虚线所示。与之前的情况相比,达到收敛所需的迭代次数大大减少(约1100次迭代对比约2850次迭代)。从中我们可以得出的结论是在Courant数(CFL数)和显式松弛之间取得平衡非常重要,以实现稳定性和收敛速度的双重目标。通过同时调整这些参数,可以在求解过程中提高效率和准确性。建议进行敏感性分析和基准实验,以确定每个具体案例的最佳组合。

耦合求解器可使用网格序列(GSI)进行加速,网格序列是在一系列粗糙网格上运行一阶欧拉方程。网格序列的默认设置适用于一般情况,如考虑亚/跨音速问题可增加GSI的CFL数值,对于具有良好GSI收敛性的问题,可调整更严格的“容差”,对于高超声速流动问题,考虑降低GSI的CFL数值,或者降低“容差”值以及增加迭代次数,如果GSI解变得不稳定(例如应用了限制方法),可减少粗糙等级的数量。
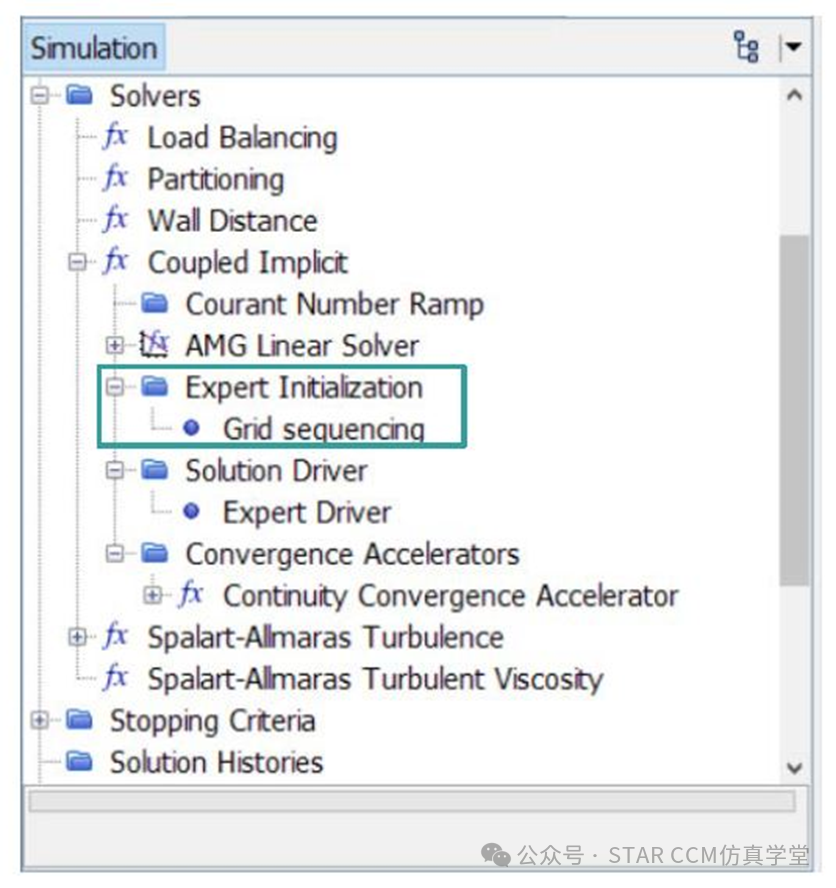
耦合求解器还可采用专家驱动程序(ED)来提供简单而稳健的收敛加速,专家驱动程序中CFL控制由线性系统稳定性确定,显式松弛控制有助于非线性稳定性,专家驱动程序默认设置效果良好,但可考虑CFL跃升,最大显式松弛对于跨音速流动,降低到0.5-0.75;对于非常严格的问题(燃烧、复杂状态方程、高超声速等),降低到0.3-0.5。
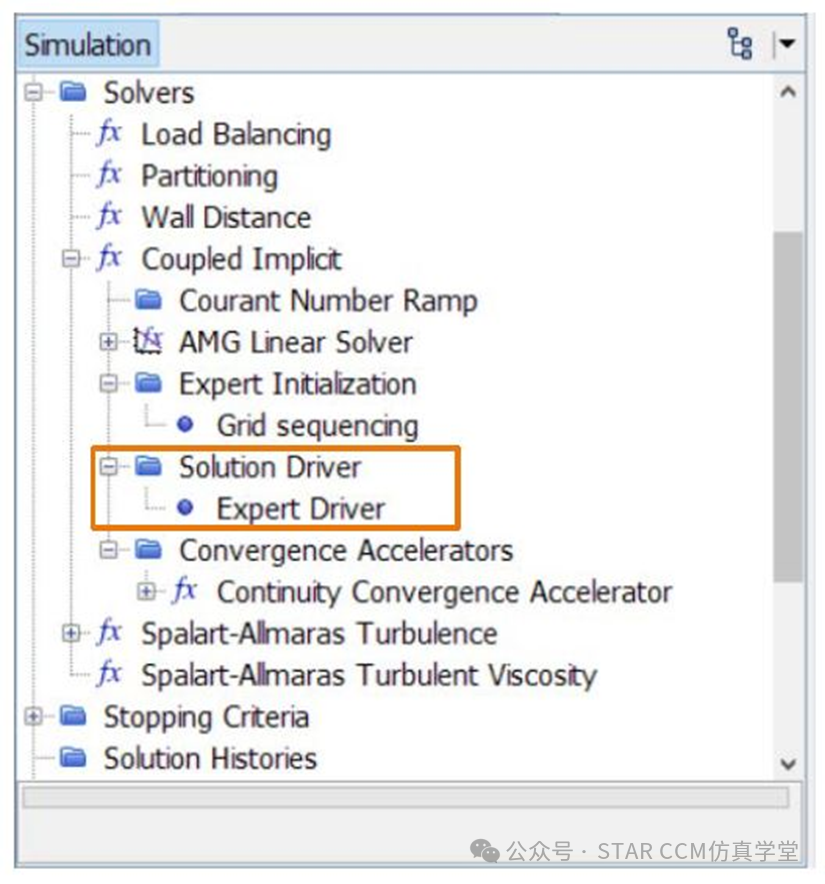
耦合求解器具有连续性收敛加速器(CCA),连续性收敛加速器解决压力修正的椭圆方程,然后通过欠松弛更新解,类似于SIMPLE中的压力修正,对于由于质量平衡收敛缓慢的问题非常有用,例如:高超声速流动、燃烧等,推荐使用默认设置,对于最困难的问题,启用“增强稳定性处理”。
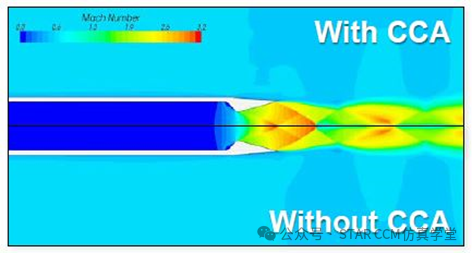

湍流总是以分离的方式求解的,运行耦合流动求解,将湍流求解器的URF(𝜔𝑡)与 CFL匹配,即𝜔𝑡=CFL/(CFL+1),如果使用低隐式松弛(𝜔𝑡→1),考虑将湍流AMG求解器更新为V循环而不是 Flex(默认设置)。在区域级别应用方向重排序可提高AMG性能,对于高超声速流动或发散的问题,在早期阶段考虑增加更多的耗散。在初始求解时可使用一阶精度,但在最终解决方案中返回到二阶精度。
以NACA0012机翼为例说明两个主要湍流求解器参数之间的相互作用:湍流URF (Turbulence URF)和湍流粘度 URF (Turbulent ViscosityURF)。
案例细节:2D测试案例,NACA0012翼型,马赫数𝑀a = 0.15,雷诺数𝑅e = 5𝑀,使用 Spalart-Allmaras(SA) 湍流模型。

在这个例子中,考察了4个不同的CFL数值,而SA湍流参数保持默认设置。Courant数在初始阶段有所帮助,但在“次级瞬态”过程中效果停滞。CFL数用于描述数值方法中的时间步长选取。它对于控制数值稳定性和模拟精度非常重要。在初始阶段较低的CFL数可以帮助系统更好地适应初始条件,并保持数值稳定性。然而,在“次级瞬态”过程中,CFL数的影响会减弱,因为系统已经进入了一个相对稳定的状态。SA湍流模型的参数根据默认设置进行保持,这意味着在测试中没有改变湍流模型的具体参数。因此,通过改变CFL数值来考察其对结果的影响,发现Courant数对于初始阶段具有一定的帮助,但在“次级瞬态”过程中,Courant数的影响逐渐减弱,可能无法产生进一步的改善。因此,在使用SA湍流模型时,仅通过调整CFL数值可能无法显著改变“次级瞬态”过程的结果。可能需要进一步考虑其他因素或改变湍流模型参数来解决“次级瞬态”过程中的问题。
在这个案例中,湍流URF和湍流粘度URF是两个需要相互调整的参数。它们对稳定性和速度之间存在权衡。如果想要获得更高的速度,可以提高湍流URF值。这样会增加湍流模型对湍流效应的计算程度,从而使求解器更快速收敛。但是,需要注意的是,过高的湍流URF值可能会引入不稳定性。另一方面,降低湍流粘度URF值可以提高稳定性,较低的湍流粘度URF值会减小湍流模型对湍流粘度的考虑程度,从而降低数值不稳定性的风险。然而,过低的湍流粘度URF值可能会导致湍流效应计算不足,从而影响最终结果的准确性。因此,在实际应用中,需要根据具体情况权衡两个参数的取值,以获得既具有良好稳定性又具有较高计算速度的求解器性能。
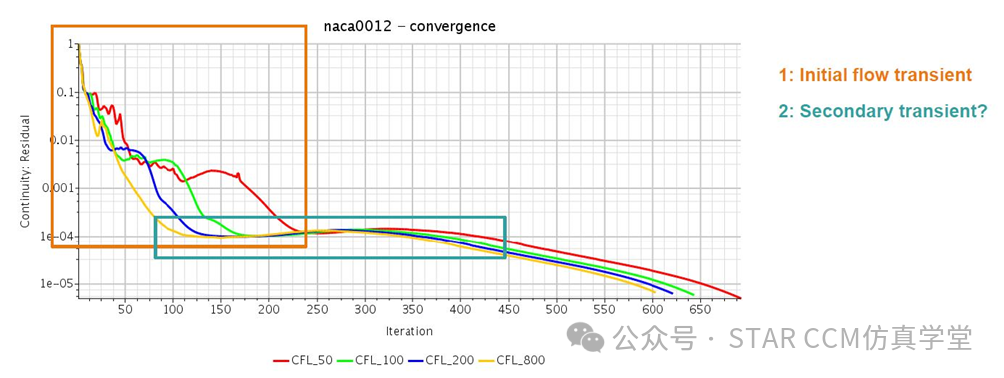
在考虑湍流求解器的隐式/显式收敛性平衡时,通过保持它们的乘积不变来进行变化。趋势显示,增加湍流的隐式松弛有助于最小化/消除次级瞬态的影响。对于CFL=200的情况,等效于湍流的隐式松弛因子约为0.995。因此为了获得更好的性能,需要平衡湍流求解器的隐式和显式松弛,并非所有情况都允许使用如此高的湍流隐式松弛因子。
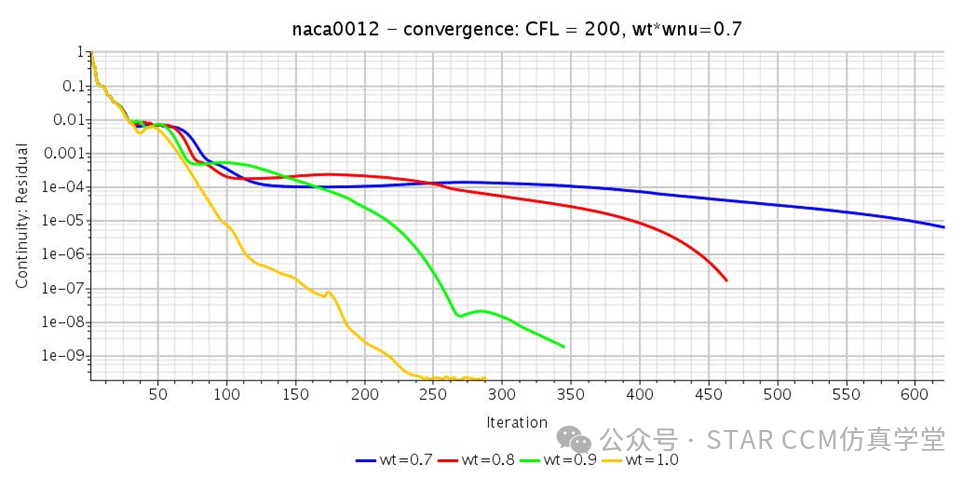
在高升力机翼中,使用CFL=400和ωe=0.5进行计算。保持隐式和显式湍流URF乘积不变,与之前的情况相比,改进效果较小,但仍然实现了10-15%的改进。这些改进的好处因情况而异,也会根据湍流模型的不同而有所差异,关键的收获是如何利用可用的工具来提高整体性能。通过调整CFL数和ωe值以及其他相关参数,可以进一步探索调整湍流模型来实现更好的性能提升。但需要注意,每个具体的案例可能会有不同的最佳参数设置。

对于外部空气动力学的不同流动区域,在所有情况下,建议使用GSI + ED(隐式求解器和显式离散化)。对于亚音速/跨音速:CFL数约为100,为获得较快的性能,CFL数可约为1000,具体取决于网格质量和物理特性。对于超音速,CFL数约为20;对于高超声速,CFL数约为1;对于全局质量平衡难以收敛的情况,考虑添加连续性收敛加速器(CCA),这种情况通常发生在具有尾流区域的超音速/高超声速案例中,在这些情况下,使用CCA可以帮助加快全局质量平衡的收敛速度。需要注意的是,以上提供的建议仅作为参考,具体的最佳参数设置还需要根据具体问题进行调整。对于不同的流动问题和模拟要求,可能需要进一步的参数研究和实验来确定最佳的性能优化策略。




