隐式Newmark动力积分算法及matlab源码
本文摘要(由AI生成):
这篇文章主要介绍了显式动力积分中心差分法的基础算法和实现过程,并提供了相关的 MATLAB 代码。文章首先回顾了之前提供的显式动力积分中心差分法基础算法的 MATLAB 实现,然后介绍了时域动力学有限元分析中常用的计算方法,包括模态叠加法和直接积分法,并详细讲解了直接积分法中的隐式积分法和显式积分法的特点和优缺点。文章还介绍了 Newmark-beta 法的具体积分公式和计算过程,并通过 MATLAB 代码进行了演示。最后,文章通过对比不同步长下显式中心差分法和 Newmark-beta 法的计算结果,展示了显式积分法的稳定时间增量步与网格密度和质量的关系。
在之前的推文显式动力学中心差分法matlab源码中,本公 众号提供了显式动力积分中心差分法基础算法的matlab实现。
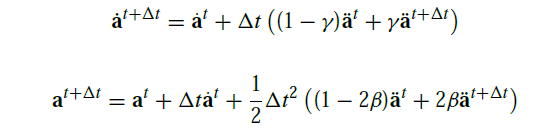
 取不同的值时,其可以得到各种不同的积分方法。例如,
取不同的值时,其可以得到各种不同的积分方法。例如, 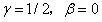 时,该积分格式即为之前提到的中心差分法。
时,该积分格式即为之前提到的中心差分法。 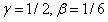 时该格式为线性加速度法。
时该格式为线性加速度法。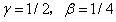 时的积分方法,此时的积分方法也称为平均加速度法。
时的积分方法,此时的积分方法也称为平均加速度法。

clcclearn=2;k=zeros(n);m=zeros(n);Cdamp=zeros(n);k=[6 -2;-2 4];m=[2 0;0 1];disp0=zeros(n,1);velocity0=zeros(n,1);acceler0=[0;0];dt=0.28; alpha=0.25;delta=0.5;a0=1/(alpha*dt^2);a1=delta/(alpha*dt);a2=1/(alpha*dt);a3=1/(2*alpha)-1;a4=delta/alpha-1;a5=dt/2*(delta/alpha-2);a6=dt*(1 - delta);a7=delta*dt;kbar=k+a0*m+a1*Cdamp;disp_0_dt=disp0-dt*velocity0+a3*acceler0;Rt_pdt=[0;10];ndtime=12;u=zeros(ndtime+1,n);t=zeros(ndtime+1,1);t(1)=0;u(1,:)=disp0;for i=1:ndtimeRt_pdt_bar=Rt_pdt+m*(a0*disp0+a2*velocity0+a3*acceler0)+Cdamp*(a1*disp0+a4*velocity0+a5*acceler0);disp_t_pdt=kbar\Rt_pdt_bar;u(i+1,:)=disp_t_pdt;acceler_t_pdt=a0*(disp_t_pdt - disp0) -a2*velocity0-a3*acceler0;velocity_t=velocity0+a6*acceler0+a7*acceler_t_pdt;t(i+1)=i*dt;disp0=disp_t_pdt;velocity0=velocity_t;acceler0=acceler_t_pdt;endfigure(1),plot(t,u(:,1),"r-"),grid on;xlabel("time");ylabel("disp_1");hold on;%legend("Newmark");figure(2),plot(t,u(:,2),"B-"),grid on;xlabel("time");ylabel("disp_2");hold on;%legend("Newmark");
最终的位移如图所示:
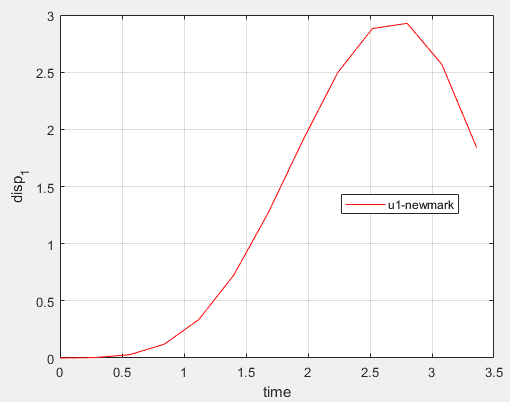
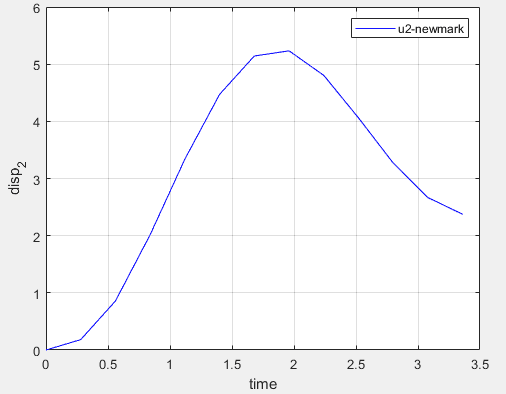
与显式中心差分法的对比:
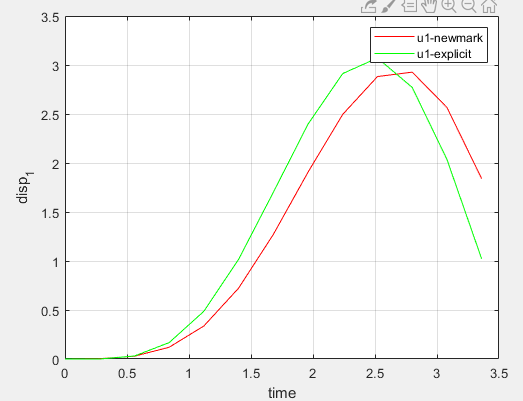

可以看出二者略有差别。
如果将步长减小至0.028,二者对比如下:
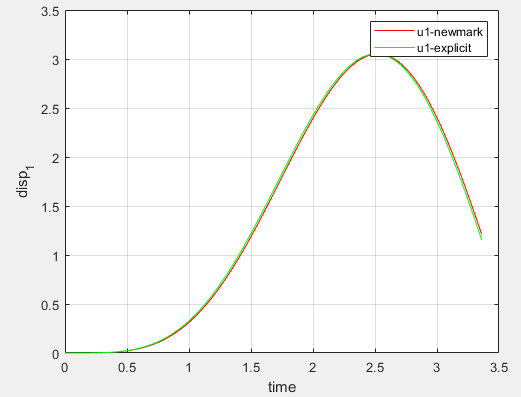
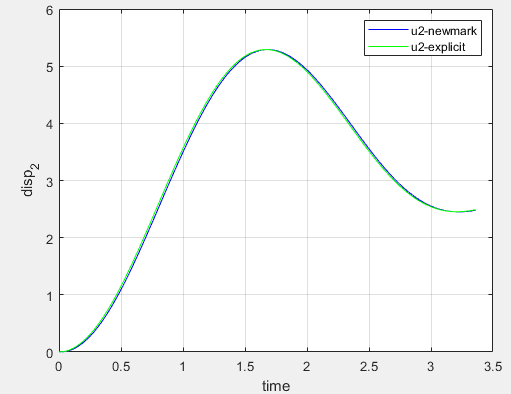
二者匹配度较好。
以上,即是本文的全部内容,感谢您的阅读!
登录后免费查看全文
著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2024-03-19
最近编辑:7月前
还没有评论
相关推荐
最新文章
热门文章




