推导出一个两端口的功率增益的表达式,需要哪些预备知识点
(1)
一个两端口的功率增益,在[1]的12.1节中给出了三种定义,分别是:
①,功率增益(power gain)=G=PL/Pin
②,可用功率增益(available power gain)=Ga=Pavn/Pavs。
③,转换功率增益(Transducer power gain)=Gt=PL/Pavs。
而对这些功率进行定义时,源,负载和管子之间的关系,可以从下面的图中,看出点道道来[2]。对于功率增益,没有定义源或者负载的匹配状态;对于可用功率增益,是定义源和负载与管子都是共轭匹配;对于转换功率增益,则是定义源与管子是共轭匹配。
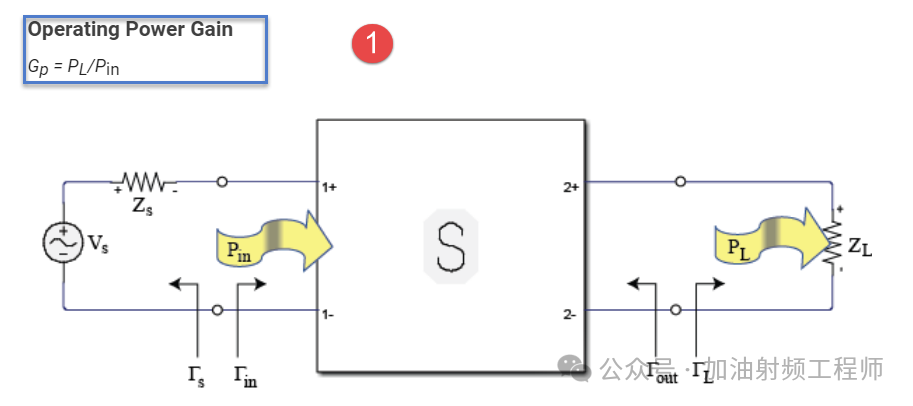
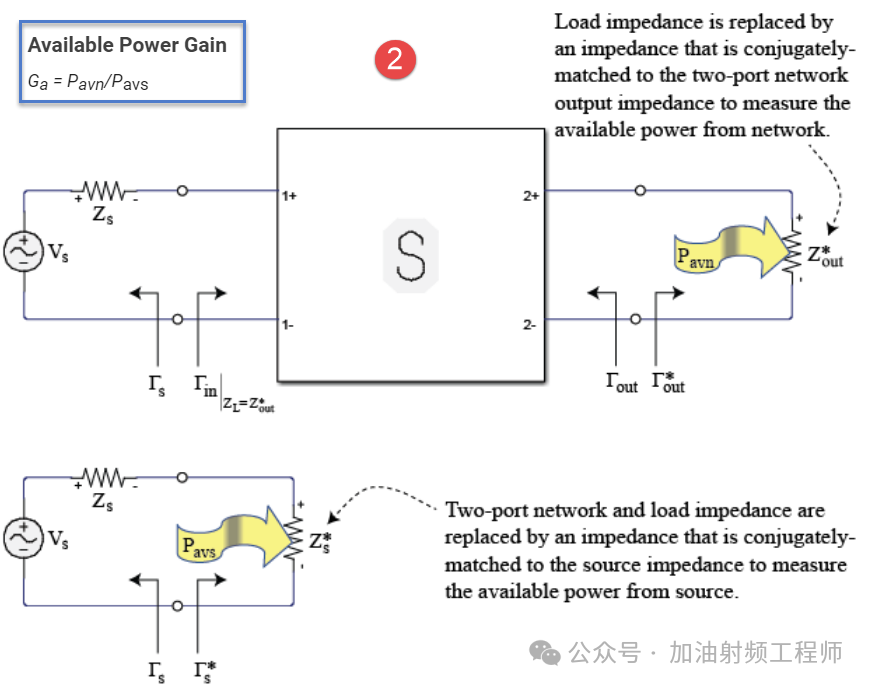
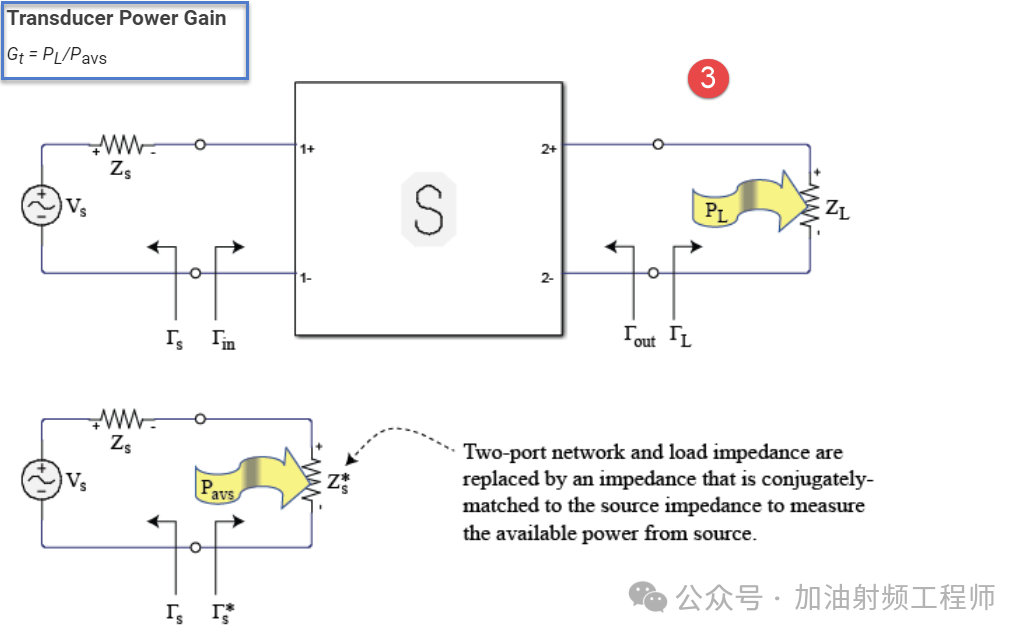
而这三个功率的表达式,分别为:

其中最有用的增益定义,是transducer power gain,是因为它包含了源和负载失配的影响。
(2)
那这几个公式是怎么推导出来的呢?
在进行推导之前,先来说一说,在推导过程中,会用到的两个知识点。
(3)
第一个,就是推导过程中,用到的反射系数与阻抗之间的关系,比如说:
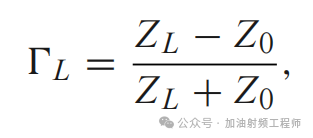
那这个关系式是怎么来的呢?
如果稍稍往前推的话,咱们可以从传输线的电报方程说起。
传输线,之所以在低频和高频的时候,会被给予不同的对待,就是因为在高频的时候,传输线的尺寸与波长可以比拟,这个时候,传输线上的电压和电流就不是恒定的,而是变化的。
打个比方,在一条路上,有一块砖头,人走在这条路上,基本可以对砖头视而不见;而如果换成蚂蚁,那可能就是一座大山;也就是说,因为人的步子很大,所以在这一步里面的路,里面不管有啥,人都不太能感知到;但是蚂蚁的步子很小,那路上的砖头就会对蚂蚁的行走,造成很大的困扰。人就对应于低频信号,其步子的大小,对应信号波长;而蚂蚁就对应高频信号。
那当信号频率比较高的时候,怎么分析传输线呢?
所以反射系数与阻抗之间的关系,大概的由来是这样的:
①,在传输线上取无限小的一段,假设长度为△z,并且将这段传输线,用R,L,C,G等来等效,并用基尔霍夫电压和电流定律列出电压电流与这些器件的关系;
②,然后得到电报方程
③,从电报方程中,推导出传输线上电压和电流的表达式
④,从电压和电流的表达式中,推导出反射系数与阻抗之间的关系。
(4)
第二个,就是射频系统中的功率的计算。
在射频系统中,相比于电压和电流,我们更在意的是功率,比如上面的增益的定义,就是功率增益[3]。
那知道电路中的电压和电流,怎么计算出功率呢?
在分析射频系统时,经常假定电压和电流都是随时间余弦或正弦变化,所以电压和电流可以用相量来表示,即:
v(t)=Re{V*exp(jwt)};
i(t)=Re{I*exp(jwt)}。
相量表示时,没有exp(jwt)和Re{}, 这是因为,大家达成了共识,虽然表达式中没写,但是大家都默认是还隐藏着这两个因子。
假设电压和电流的表达式如下图所示,则可以推导出,当v(t)和i(t)有相位差的时候,其平均功率的表达式。

(4)
接下来,就可以推导功率增益的那些表达式啦!
假设电压,电路,以及其他参数的定义如下图所示:

那么:

然后考虑共轭匹配,可以得到GA和GT。
参考文献:
[1] David M. Pozar, Microwave Engineering
[2] Calculate power gain from two-port S-parameters - MATLAB powergain - MathWorks United Kingdom
https://uk.mathworks.com/help/rf/ref/powergain.html
[3] Analysis of Power and Phasor in RF systems - Rahsoft
https://rahsoft.com/2021/04/07/analysis-of-power-and-phasor-in-rf-systems/




