Abaqus血管支架仿真|材料模型和参数
本文摘要(由AI生成):
文章主要介绍了线弹性-塑性材料、超弹性材料、镍钛诺材料等在Abaqus/CAE中的定义和应用。线弹性-塑性材料用于金属制成的气球扩张支架材料,超弹性材料用于血管模型,镍钛诺材料具有超弹性和超弹-塑性特性,可用于自扩张支架。
1. 线弹性-塑性材料
线弹性-塑性材料模型对于金属为典型单轴应力-应变,用于由各种金属和金属合金制成的气球扩张支架材料,比如不锈钢、钽、铂合金、铌合金、钴合金等。
当载荷低于屈服点时,大多数金属行为近似为线弹性,在Abaqus/CAE中定义如下。

▲ 弹性性能定义
线弹性-塑性材料模型,如应力大于屈服应力,则大多数金属开始塑性变形。常用Mises屈服准则,用于屈服属性表现为初始各向同性的金属。其塑性变形导致的屈服面演化的硬化规律有1)各向同性硬化的理想塑性,常用于一般研究应用,以及2)运动硬化、耦合各向同性/运动硬化,适用于循环载荷的应用。在Abaqus/CAE中定义如下。

2. 超弹性材料
通常用于放置支架的血管模型。试验血管通常采用各向同性超弹性材料建模,而管腔切片通常是各向异性的,因胶原纤维通常呈螺旋状排列。Abaqus提供了各向同性和异性超弹性材料模型。

▲ 血管结构【1】
[1] G.Holzapfel,et al, “A New Constitutive Framworkfor Arterial Wall Mechanics and a Comparative Study of Material Models,"Journal of Elasticity, vol. 61, 2000, pp. 1-48.各向同性的超弹性材料模型有物理激励模型和唯象模型两大类,通常采用唯象模型。具体区别如下。

▲ 各向同性超弹性材料模型
注:唯象理论(phenomenology),是指物理学中解释物理现象时,不用其内在原因,而是用概括试验事实而得到的物理规律。唯象理论是试验现象的概括和提炼,没有深入解释。
Abaqus/CAE内定义各向同性的超弹性参数如下图。具体操作可参考《Abaqus工程实例详解》。


▲ 超弹性定义
Abaqus/CAE能够根据测试参数自动评估超弹性材料模型,用以验证预测性能和试验数据的相关性。根据实验数据,绘制预测的名义应力-应变曲线,可对比不同超弹性模型与测试数据。

▲ 自动评估拟合超弹性材料模型
各向异性的超弹性材料模型,有Generalized Fung形式 、Holzapfel-Gasser-Ogden形式,以及用户自定义应变能形式。具体案例和解释将在视频中作以说明。
▲ 各向异性超弹性[2]
[2] T.Gasser, et al, “Hyperelastic modeling of arterial layers with distributedcollagen fibreorientations," J. R. Soc. Interface, vol. 3, 2006, pp. 15-353. 镍钛诺材料
镍钛诺是由相等或几乎相等含量的镍和钛组成的合金,其关键特征有:1)超弹性,由奥氏体相和马氏体相之间的应力诱导转变,可逆变形可达到非常高的应变(高达10%);2)形状记忆,在同一温度下进行变形,加热到超过转变温度后恢复原状,这一属性不用于支架;3)优良的疲劳性能;4)生物相容性;5)对温度敏感。
镍钛诺具备超弹性材料模型和超弹-塑性模型。超弹性材料模型:用于镍钛合金自膨胀支架,大多数自扩支架应用于镍钛诺的超弹性极限内。超弹-塑性模型:用于加载超过超弹性极限的自扩张支架,通常塑性变形是由气球的进一步膨胀引起。镍钛静止状态,材料以奥氏体呈现,超过一定应力奥氏体相转变为马氏体,产生大应变的同时,应力几乎没有增加;在卸载后,材料在较低的转变应力下转变回奥氏体相;进一步超过超弹性极限后,马氏体呈现塑性行为。
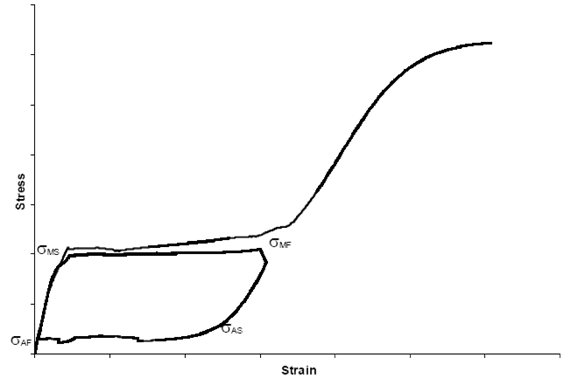
▲ 单轴拉伸镍钛诺管,典型的镍钛诺应力-应变图 [3]
[3] S. Gopal, et al, MEDInstitute Incorporated, a COOK Group Company, "Fatigue Life Estimation ofNitinol Medical Devices," Abaqus Users' Conference, Newport, Rhode Island,May 2008, pp. 438-446.镍钛诺材料模型,镍钛诺性能不符合任一传统的本构方程,现在使用的镍钛诺材料模型是唯象的。

▲镍钛诺材料模型
基于Auricchio和Taylor[4,5,6]的材料模型可以在Abaqus中使用,超弹性和超弹-塑性模型,都作为内置的Abaqus功能。
[4] AuricchioF., Taylor R.L. “Shape-memory alloys: modeling and numerical simulations of thefinite-strain superelasticbehavior”. Comp. Meth. in Appl. Mech. and Engnrg.1996; 143: 175-194.
[5] AuricchioF., Taylor R.L., Lubliner J. “Shape-memory alloys: macromodelingand numerical simulations of the superelasticbehavior”. Comp. Meth. in Appl. Mech. and Engnrg.1997; 146: 281-312.
[6] QidwaiM.A., LagoudasD.C. “Numerical implementation of a shape memory alloy thermomechanicalconstitutive model using return mapping algorithms”. Int. J. Num. Meth. Engnrg.2000; 47: 1123-1168.
作为内置的用户材料,不需要Fortran编译器或子程序文件;Abaqus/Standard中,材料名称必须以ABQ_SUPER_ELASTIC开;Abaqus/Explicit中,材料名称必须以ABQ_SUPER_ELASTIC_NxD开头,x表征单元的维度 (例如,x= 3为实体单元);超弹性或超弹-塑性材料模型的选择,取决于材料常数的个数。超弹性、超弹-塑性性能于Abaqus/CAE应用和验证,见下图。

▲ 超弹性性能验证
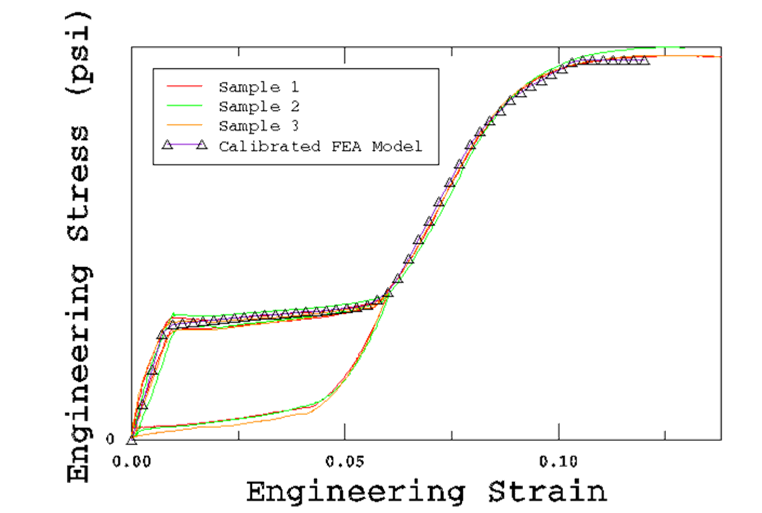
▲ 超��-塑性性能验证
4. 总结
默认情况下,Abaqus的单元不计算沙漏刚度,对于镍钛诺材料,如果使用其,必须指定沙漏控制刚度,同时,如果镍钛诺材料模型用于剪切柔性壳或梁单元,则必须指定横向剪切刚度。具体操作,后续视频演示。