2024年2月25日~2月28日，Geo-Congress 2024如期在加拿大温哥华举行，本次会议最重要的讲座---太沙基讲座【太沙基讲座(Terzaghi Lecture, 1963-2024)】由MIT的Andrew J. Whittle教授呈现，他的讲座题目是《Soil Models in Prediction, Design and Geotechnical Problem Solving (预测、设计和解决岩土工程问题中的土模型)》，全程演讲大约1小时10分钟，《计算岩土力学》公 众 号已经录制了这个讲座，同时也录制了另外3个讲座，包括Seed讲座、Peck讲座和Prakash讲座。 

3. MIT-S1土本构模型

Andrew J. Whittle对岩土工程的重大贡献之一是发展了所谓的"MIT-S1"土本构模型，这是本次太沙基讲座的其中一个重点。MIT-S1土本构模型是一个在文献中很少提及的土本构模型，MIT-S1是MIT在上世纪90年代开发的一个模型。MIT-S1模型与NorSand模型【FLAC3D的NorSand模型】一样，其主要用途是进行静态液化分析。

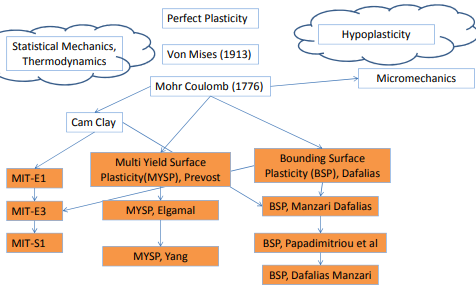MIT-S1似乎是在Ramberg-Osgood模型的基础上改进的。大多数与岩土相关的工业软件都内置了Ramberg-Osgood模型，例如Adina, OpenSees, FLAC3D, GTS NX, Diana, Abaqus。

MIT-S1模型是一种广义有效应力土模型，用于对砂土行为进行本构模拟。该模型可对静态液化的敏感性进行定量预测，考虑了砂土初始状态对潜在排水不稳定性的影响，预测各种土与速率无关的各向异性行为，它对捕捉中间土行为特别有效。

MIT-S1的主要特性如下： 

(1) 强调了砂土初始状态对潜在排水不稳定性的影响。

(2) 预测与速率无关的土行为。

(3) 预测各向异性行为，即与方向有关的土行为。

(4) 可用于多种土。

该模型已成功用于各种模拟，并显示出极佳的简易性，它在各种应力水平和空隙率下使用相同的参数，并采用了临界状态土力学概念。不过，值得注意的是，该模型并不能预测循环载荷作用下的渐进破坏（应力-应变特性的变化主要归因于超孔隙压力的增加）。

(1) 了解空隙率、固结历史和材料各向异性的影响。

(2) 认识到只有采用适当的模拟策略，才能捕捉到排水条件变化引起的潜在不稳定性。

(3) 认识到某些简化假设会对潜在的不稳定性产生不切实际的限制。

参数值是通过使用其它软件模拟并与实验室的排水直剪(UDSS)试验数据进行比较而得出的。校准优先考虑与一维压缩相关的 MIT-S1 模型参数，以及在剪切时从收缩行为到扩张行为的过渡。

4. 参考

下面的这些参考文献仅来自GeotechSet数据集，没有参考任何外部文献。

[4] (1993) The effects of installation disturbance on interpretation of in-situ tests in clay.【Hoek-Brown模型扰动因子(Disturbance Factor D)的衰变研究】

[5] (1994) Model Prediction of Anisotropic Behavior of Boston Blue Clay.【各向异性岩体的数值模型(Anisotropic Rock Mass Model)】

[6] (1994) Stress-deformation behavior of an embankment on Boston blue clay.【[文献]利用软土蠕变模型预测路堤沉降(Soft Soil Creep model)[10/22/2020]】

[7] (1994) Formulation of MIT‐E3 Constitutive Model for Overconsolidated Clays.

[8] (1995) Compression model for cohesionless soils. 【无粘结性土地基的沉降计算方法(Immediate Settlement in Cohesionless Soil)】

[9]  (1998) Undrained limit analysis for combined loading of strip footings on clay.【[最新文献]循环单轴和三轴剪切的液化阻力: 一个比较研究 [11/8/2020]】

[10] (1998) Time effects in the compression of sands. 【隧道纵向变形曲线 LDP (Longitudinal Deformation Profile)】

[11] (1999) Formulation of a unified constitutive model for clays and sands.【岩石脆性破坏和断裂扩展的DFN-FDEM分析】

[12] (1999) Role of finite element methods in geotechnical engineering.【使用自定义的岩土数据(GeotechSet)增强ChatGPT的回答能力】

[13] (2000) Base Stability of Deep Excavation in Anisotropic Soft Clay.【各向异性线性强度模型(Anisotropic Linear Strength Model)】

[14] (2000) Role of undrained strength anisotropy in stability analyses.【UJRM数据集---Ubiquitous Joint Rock Mass Modelling】

[15] (2000) Model for dynamic shear modulus and damping for granular soils.【zone mechanical命令】

[16] (2001) Prediction and interpretation of pore pressure dissipation for a tapered piezoprobe.【设置初始孔隙压力(Pore Pressure)】

[17]  (2002) Evaluation of a constitutive model for clays and sands: Part I - Sand behaviour.【第62届朗金讲座 | Lidija Zdravkovic教授---岩土工程中的数值方法】

[18] (2003) Calculations of bearing capacity factor Nγ using numerical limit analyses.【纪念 | 现代岩土工程领域的教育家和多产作家---Dr. Braja Das(1941-2023)】

[19] (2003) Undrained stability of braced excavations in clay.【使用非排干脆性指数粗略估算静态液化(undrained brittleness index)】

[20] (2007) Nicoll Highway collapse: Evaluation of geotechnical factors affecting design of excavation support system.【第五届土力学和岩土工程新进展国际会议(岩土工程课程outline)】

[21]  (2011) Bearing Capacity of Spatially Random Cohesive Soil Using Numerical Limit Analyses.【隧道开挖稳定性概率分析(Probabilistic analysis of tunnel stability)】

[22] (2013) Evaluation and Prediction of 17th Street Canal I-Wall Stability Using Numerical Limit Analyses.【尾矿坝破坏原因的不同解释】

[23] (2013) Model prediction of static liquefaction: influence of the initial state on potential instabilities.【使用非排干脆性指数粗略估算静态液化(undrained brittleness index)】

[24] (2016) Effect of spatial variability on the slope stability using random field numerical limit analyses. 【新的监管环境下矿产资源及其不确定性的地质统计学评价】

[25] (2018) A novel elasto-viscoplastic formulation for compression behaviour of clays.【压缩指数Cc的经验估算---与初始孔隙比e0的回归关系】

[26] (2021) MIT-S1 Constitutive Model Calibration for a Portland area Soil. 

[27] (2022) Stability Analysis of Upstream Tailings Dam Using Numerical Limit Analyses.【尾矿坝破坏原因的不同解释】

[28] (2023) Numerical modeling of static liquefaction in tailing dams - comparison between HSS, Norsand, and MIT-S1 constitutive models. 

[29] Selection of Material Parameters for Sands using the MIT-S1 Model.