边界条件专题(对角元素置“1”法、乘大数法、划行划列法、拉格朗日乘子法、罚函数法)
在求解整体刚度方程时,一定要考虑已有的边界条件,排除系统的刚体 位移,才能求解节点的未知位移,常见的边界条件有以下三种形式:
换句话说,就是:
力加载 位移加载 多节点自由度耦合
本节分享的内容就是针对以上三种常见的边界条件形式,逐一给出求解方法,理论来源于曾攀老师的《有限元分析基础教程》和徐荣桥老师的《结构分析的有限元法与MATLAB程序设计》,想要深入了解的小伙伴也可翻阅相关文献进行深耕。
划行划列法
现考虑只有6个自由度的整体刚度方程:
假设1号自由度和4号自由度位移为: ,针对每个已知的边界条件,改变相应的行、列元素,其余位置的载荷列阵也要跟着变化,读者可自行验证该矩阵变换的正确性。
"划行划列"法的特点:
既可以处理力加载的情况也可以处理位移加载的情况 保持原刚度矩阵的规模不变,不需重新排序 保持整体刚度矩阵的对称性,利于计算机的规范化处理
数值实现
for i=1:nconstrain
n=constrain(i,1);
d=constrain(i,2);
m = (n-1)*2 + d;
FFG = FFG - constrain(i,3) * KKG(:,m);
FFG(m) = constrain(i,3);
KKG(:,m)=zeros(nnode*2,1);
KKG(m,:)=zeros(1,nnode\*2); KKG(m,m) = 1.0;
end
对角元素置"1"法
假设第3个自由度位移为0,即 ,这时的矩阵对应的对角元素为1,该行和该列的其余元素为0,载荷列阵的相应元素也为0。
对于第3行: 。
对角元素置"1"法的特点:
只能处理力加载的情况 保持原刚度矩阵的规模不变,不需重新排序 保持整体刚度矩阵的对称性,利于计算机的规范化处理
数值实现
for i=1:nconstrain
n=constrain(i,1);
d=constrain(i,2);
m = (n-1)\*2 + d;
KKG(m,:)=0;KKG(:,m)=0;
KKG(m,m)=1; FFG(m)=0;
end
乘大数法
假设第4个自由度位移为 ,即 ,这时刚度矩阵对应的对角元素为乘以一个大数 ,载荷列阵的相应元素置为 。对于第4行:
由于,则上式变为:
即 。
乘大数法的特点:
既可以处理力加载也可以处理位移加载的情况 保持原刚度矩阵的规模不变,不需重新排序 保持整体刚度矩阵的对称性,利于计算机的规范化处理 数值精度与大数的取值有关,太小了精度差,太大了容易出现"矩阵奇异"的现象
数值实现
for i=1:1:nconstrain
n = constrain(i,1);
d = constrain(i,2);
m =(n-1)*2 + d ;
FFG(m) = constrain(i,3)* KKG(m,m)* 1e8;
KKG(m,m) = KKG(m,m) * 1e8;
end
拉格朗日乘子法
当存在多点之间的约束耦合关系时,就会出现带约束方程的表达式,其一般数学表达式可以写成:
也写成矩阵相乘的形式: ,注意 是一个约束系数矩阵, 是一个载荷列向量, 是一个约束系数列向量。
假设二维模型中2号节点与3号节点的1、2自由度绑定,即:
此时的 和 将变为:
扩充至原刚度矩阵中,原刚度方程将变为:
即
以上示例是"两对自由度"进行耦合约束,对于更多节点更多自由度的耦合也是相同的道理,扩充相应列向量即可。
拉格朗日乘子法的特点:
可处理多节点、多自由度约束的情况 原有刚度矩阵的维数会随着耦合的自由度对数的增加而增加 计算精度良好
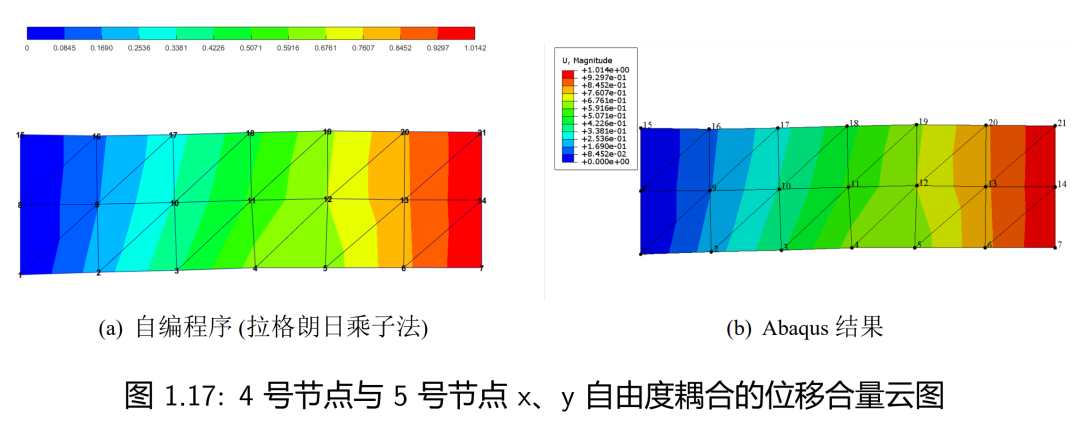
本文以二维平板模型单侧受拉为例,所用单元类型为常应变三角形单元,将4、5号节点两个自由度进行耦合约束,即U4X=U5X,U4Y=U5Y。自编程序与Abaqus的MPC约束求解精度对比总结于下表,从表中可以看出两者的求解精度几乎保持一致;位移云图对比如下图所示,从图中可以看到4、5号节点的位移量是一致的,导致云图发生曲折变化。
| 求解技术 | U4X | U5X | U4Y | U5Y |
|---|---|---|---|---|
| 拉格朗日乘子法 | 0.60501246 | 0.60501246 | 0.16898998 | 0.16898998 |
| Abaqus | 0.60501200 | 0.60501200 | 0.16899000 | 0.16899000 |
数值实现
详见《有限元基础编程百科全书》
罚函数法
该方法将引入一个较大的系数来形成一个罚函数(penalty functionapproach),原刚度方程 将转换为 和 ,其中 是引入的罚系数。
罚函数法的特点:
可处理多节点、多自由度约束的情况 保持原刚度矩阵的规模不变,保留原有的对称性 计算精度与引入的罚系数大小有关
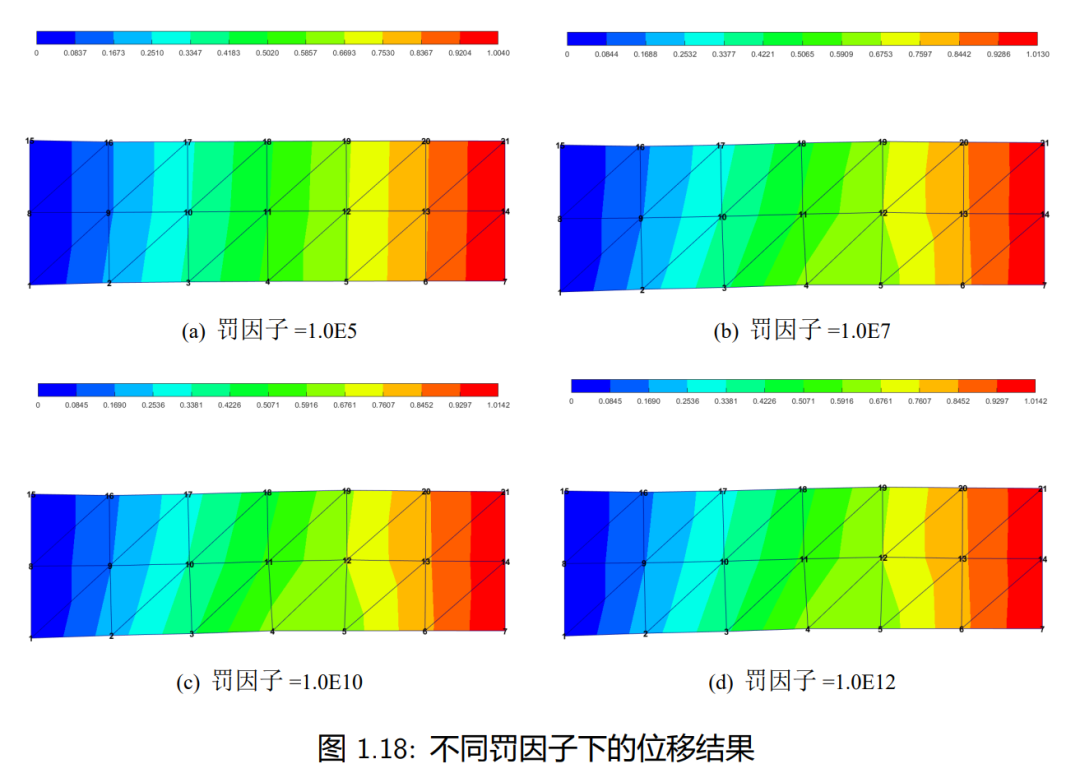
虽然引入大数后可以较为巧妙地解决多自由度耦合问题,但是往往这种方法 会因为大数的取值影响求解精度,本小节将简要讨论罚系数的取值具体有多影响求解精度。
下表是取不同罚系数时,4号节点和5号节点的位移变化,从表中可以看出,随着罚系数的增大,数值结果越来越接近Abaqus结果,但是真的是越大越好吗?在我们实际编程中,当罚系数很大很大时,将会产生矩阵奇异性,也会影响结果精度,所以大数的取值是个值得思考的事情。
| 罚因子 | U4X | U5X | U4Y | U5Y |
|---|---|---|---|---|
| 1.0E5 | 0.51428996 | 0.66002949 | 0.08409077 | 0.08628681 |
| 1.0E7 | 0.59764201 | 0.60909211 | 0.16201780 | 0.16140338 |
| 1.0E10 | 0.60500453 | 0.60501683 | 0.16898248 | 0.16898178 |
| 1.0E12 | 0.60501238 | 0.60501250 | 0.16898991 | 0.16898990 |
| Abaqus | 0.60501200 | 0.60501200 | 0.16899000 | 0.16899000 |
数值实现
详见《有限元基础编程百科全书》


