《有限元仿真实践原理》有限元分析基本原理
本文摘要(由AI生成):
在工程问题求解中,选择合适的方法至关重要。解析法适用于简单问题,提供精确解;数值计算法如有限元分析,适用于复杂问题,通过近似计算得出解;实验法则在物理样机可用时非常有效。每种方法各有优势,需结合具体情况选择。在实际应用中,可综合使用多种方法求解同一问题,以达到最佳效果。有限元分析以其结果可视化及预测潜在故障位置的能力,在工程设计中占据重要地位。选择合适的求解方法,能有效解决复杂工程问题,为实际应用提供可靠方案。
解决所有工程问题的方法
解析法 | 数值计算法 | 实验法 |
- 经典(分析)法 - 精确解 - 闭合解 - 只适用于简单的问题,如悬臂和简支梁,等等。 - 一套完整的方法 | - 数学公式 - 近似解 - 即使物理样机不可用也同样适用(初步设计阶段) - 现实生活中复杂的问题 - 不能盲目相信计算结果,使用实验法或手算法来了解结果的范围
| - 实测 - 耗费时间,且设备昂贵 - 物理样机可用时才适用 - 不能盲目相信计算结果,至少要测试3-5个物理样机 |
即使求解方案是非闭合的,该方法也能够给出相近的结果,但是在总体上仍被视为闭合解,即精确解。 | 有限元分析:线性分析、非线性分析、屈曲分析、热分析、动态分析和疲劳分析 边界元分析:声学分析和NVH性能分析 有限体积法:CFD计算流体动力学和CEM计算电磁学 有限差分法:热解析法和流体流动解析法(与有限体积法相结合) | - 应变仪 - 光弹性分析 - 振动测试 - 温度和压力传感器等 - 疲劳测试 |
处理解析或数值计算问题的步骤
解决解析和数值计算问题的两个步骤:
步骤一:写出控制方程---问题定义,也就是用数学方程描述问题。
步骤二:数学(方法)求解控制方程。
最终结果是将第一步和第二步综合起来,当这两个步骤(解析法)都没有近似解时则结果为100%准确。
数值计算法在步骤一和步骤二中采用近似法,因此所有的数值计算法结果都是近似解。
分析中的“近似” | 数值计算中的“近似” | |
步骤一 | 微小或无近似 | |
步骤二 | 微小或无近似 | |
精确度 | 高精确度结果 | 近似结果 |
数值计算方法简介
1)有限元法(FEM)
有限元法是最广泛的计算方法。
应用:线性分析、非线性分析、屈曲分析、热分析、动态分析和疲劳分析等,我们在后面的章节进行探讨。
FEA和FEM是否相同?
有限元法(FEM)和有限元分析(FEA)二者意思相同。“FEA”多用于工程行业,而“FEM”多用于高校。FEA/FEM和与其相似却不同概念的FMEA(失效模式与影响分析)之间很容易产生混淆。FEA/FEM通常只用于设计或研发部门,而FMEA在很多部门都可以使用。
2)边界元法(BEM)
这种强大的解析法能够高效地解决声学分析或NVH问题。如有限元法一样需要节点和单元,但顾名思义,它只参考域的外边界。所以当求解对象是一个体时,只考虑最外表面。如果属于一个区域,只参考最外围。这样,通过降低一个维数而更快速地解决问题。
3)有限体积法(FVM)
大部分的计算流体动力学(CFD)软件都是基于有限体积法。有限体积法只参考单位体积(同有限元分析中的单元相似)。节点上的变量属性包括压力、速度、面积、质量等,是基于二维Navier-Stokes方程(质量、动量和能量守恒平衡方程)。
4)有限差分法(FDM)
有限元法和有限差分法有很多相似之处。通常有限差分法是指求解微分方程的一种方法。它使用Taylor级数将微分方程转换为代数方程。在转换过程中忽略高阶项。与边界元分析或有限体积法结合来解决热学分析和计算流体动力学耦合问题。
是否可以利用以上列出的所有方法(FEA、BEA、FVM、FDM)来解决同一个问题(例如悬臂问题)?
答案是“YES”!而其区别在于所达到的精确度、编程的难易程度以及得出结论的时间。
当需要内部细节时(如3-D对象内部的应力)BEM边界元法得出的结果很糟糕(由于它只考虑外边界),因而需要采用FEM、FDM或者FVM。FVM用于解决应力问题,同时又适合计算流体动力学。FDM在解决复杂几何、不同材料组件以及不同类型的单元组合(1-D、2-D及3-D单元)的问题时存在局限性。而FEM在这些问题上远远优于其他竞争者。
离散化问题
现实生活中所有的对象都是连续的。也就是说,任意两个连续的粒子之间没有物理缺口。根据材料学,任何物体都是由粒子、粒子的原子、原子的分子等构成,在吸引力的作用下结合在一起。解决一个现实中连续材料的问题是很困难的。所有数值计算法的基础是以离散化(非连续)来简化问题。也就是说,节点和原子的工作原理一样,相互之间的缺口被一个称之为单元的物体来填充。在节点进行计算,结果将会插值到单元。
所有的数值计算法,包括有限元分析都遵循离散化的方法。网格(节点和单元)是无限个自由度转化到有限个自由度,也即是用有限个离散的点来代替原来连续的系统空间。
什么是自由度?
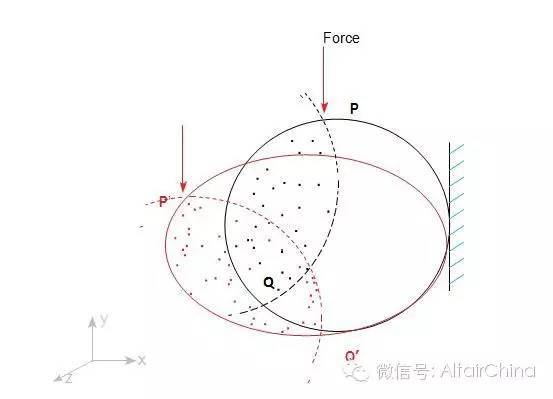
在上面所给出的例子中,一个对象被固定在一点,并在P点施加了一个力。由于受到外力,对象产生形变,P点也移到了P’点。
何时我们才能说我们知道上述问题的解决方案?
当且仅当我们能够完全定义每一个粒子的变形位置。
完全确定一个物体在空间位置所需要的参数(运动、坐标、温度等等)的最小数被称作自由度 (dof)。
思考下面的二维(平面)问题。假设已知起点在左下角。参照起点,如果要完全确定A点的位置需要两个参数,即x1和y1,也就是2个自由度(平移x和y)。
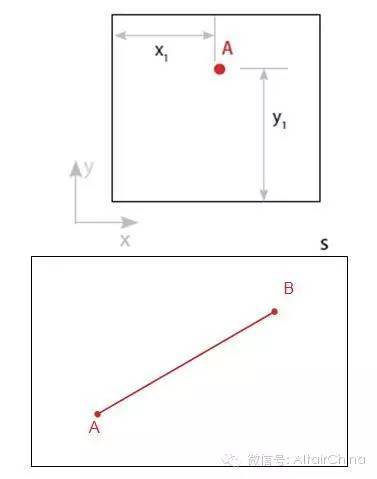
假设A点和B点被移出平面,这条线相对于三条轴自由旋转。完全确定A点的位置需要至少6个自由度3个平移(Ux , Uy , Uz)和3个旋转(θx , θy , θz)}。
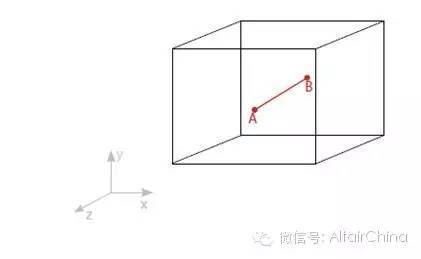
自由度是一个非常重要的概念。在有限元分析中用它来代替个体的计算点。一个给定的网格模型的自由度总数相当于节点数乘以每个节点中自由度的数量。
并不是所有单元的每个节点都有6个自由度。自由度的数量取决于单元的维度(一维、二维、三维)、种类(薄壳、平面应力、平面应变、膜壳等)以及分析类型。例如,在结构分析中,一个薄壳单元上的每个节点拥有6个自由度(位置未知,3个平移和3个旋转),同样的单元在热分析时每个节点只有一个自由度(温度未知)。
对于一个初学者了来说可能有些复杂,实际上在给不同的单元类型分配特定数量的自由度背后包含着许多逻辑、工程以及数学思想。
为什么进行网格划分?什么是有限元法?
FEM
- 一种数值计算法
- 一个实际问题的数学体现
- 近似法
有限元法只在数量有限的点时进行计算,然后将结果插值于整个域(表面或体)。
有限 – 任何一个连续的对象都有无限个自由度,在这种情况下是无法解决问题的。通过离散化和建立网格(节点和单元),有限元法把无限个降低到有限个自由度。
单元 – 所有的计算都在有限数量的点即节点进行。加入节点形成一个特定形状的实体,例如三角形或四边形,被称为单元。在任意计算点之间,会根据单元的形状运用插值函数获得一个变量的值(如位移)。
方法 – 所有的工程问题都可以用3种方法解决。有限元分析属于数值计算法。
如何从少数的计算点插值结果?
可以肯定的是有限元分析在有限数量的点进行计算,但问题是它如何在计算点之间计算未知点的值。
可以通过插值获得。请思考下图所示的一个4个节点的四边形单元。一个四边形单元可以使用下面这个线性插值公式:u=a0+a1x+a2y+a3xy
如果计算点(节点和元素)数量增加,精确度如何?
通常情况下,计算节点数量增加,精确度也会增加。
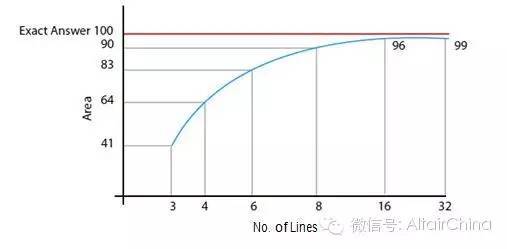
假设给你3条直线,要求你在一个圆内选出最合适的位置,并计算出三角形的面积然后与圆的面积进行比较。接着重复进行4,6,8,16,32和64条线这几种情况的比较。
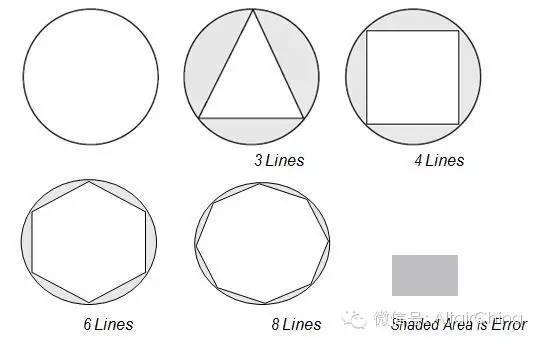
通过增加线条实现误差范围的减少。直线的数量可看作有限元分析中单元的数量。
此处圆的面积(π r2)确切值为100。三角形的面积为41,四边形的面积为64,以此类推。答案41或64不是全部适用,但是80或90则考虑了计算成本并体现了相应的设计理念。
既然节点和单元的数量越多,精确度越高,那么为什么不使用最大量的节点和单元建立一个精细的网格?究其原因是解决方案的时间同(dof)n是成正比的,n可以是1到4之间任意一个数,这取决于分析和求解器的类型。同时,由于显卡内存限制,大规模的模型在计算机上难以处理。分析人员需结合现有硬件资源,在期望精确度和能够处理的单元尺寸(间接决定dof数量)之间获得平衡。
假设使用解析法花费一个月的时间得到非常接近100的结果,那么有限元分析运用合理的网格尺寸能够在一天之内得到90的计算结果。在工业上,快速的、符合逻辑且合理的解决方案远比绝对精确要重要。
有限元分析的优势
结果可视化:对于简单的几何形状,如简支梁或悬臂梁,很容易实现某点的最大应力和位移的可视化。但是在现实工程中,具有复杂几何形状的零部件或装配件都是由不同材料不连续的对象构成,多变的约束和复杂的载荷随着时间和作用点的变化而变化。并且会随着残余应力和连接处的焊接等变得更加复杂。正因为如此,很难预测故障位置。想象一下,如果有人给你一个复杂的发动机缸体,要求你根据已给的受力情况预测故障的位置。除非你在相关领域有丰富的经验,否则很难成功预测出。但是借助CAD和CAE这样的工具,以适当的方式建模,就能很容易获得应力等高线图,清晰地看到高应力区域和位移的大小。
以前,零部件都是由经历很多测试和失效形式的经验丰富的工程师进行设计。现在,在大多数机构中,设计工程师都很年轻,他们使用像CAD/CAM/CAE这类的工具,能够帮助他们提升自信。





