【HyperMesh宝典】 苹果、雪花、蒲公英竟然可以这么玩?
本文摘要(由AI生成):
本文分享了今年Altair技术大会RADIOSS颁奖晚宴上的技术案例。文章回顾了香蕉仿真案例,并引入苹果实心旋转体仿真方法,强调切分处理的重要性。同时,文章介绍了雪花模型构建,突出几何对称性在网格划分中的应用。最后,以蒲公英模型为例,探讨了复杂模型的六面体分块原则。这些案例展示了仿真领域处理不同几何体的技巧,鼓励读者利用周末时间学习和实践,提升仿真能力。

参加过今年Altair技术大会的朋友一定都还记得RADIOSS颁奖晚宴上那个香蕉仿真的案例吧。
均衡营养,吃完香蕉,接下来让我们看看苹果怎么吃~
苹果--实心旋转体
苹果--实心旋转体
真·apple
1/8 球
1/4 圆锥
仿真apple
苹果对应的是实心旋转体的处理。实心旋转体由于在旋转轴附近的单元会退化为五面体,而且质量通常很差,所以一般的处理方法是先将实心旋转体切分为空心旋转体+沿着轴向拉伸的拉伸体。典型的如球体、圆锥、圆台等。
这么逼真的苹果是solidThinking Evolve工程师提供的哦~

一口吃掉大苹果之后,是不是想休息一下,那下面我们来看点风景吧~
雪花--对称性的利用
雪花--对称性的利用
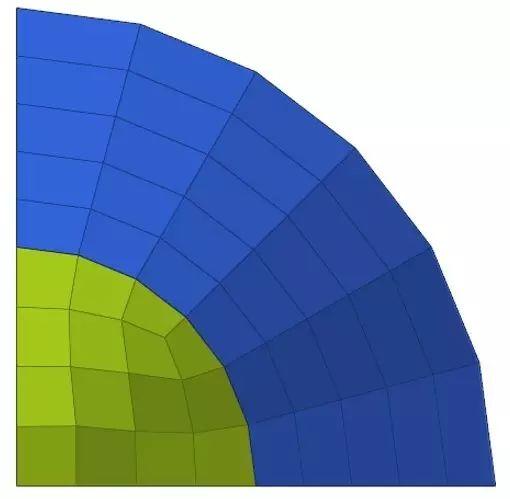
为了减少六面体网格划分的工作量,同时使对称的结构有对此的网格。在可能的情况下要尽可能地利用几何的对称性,具体而言:
只要是对称的结构,只取对称的最小一个单元来划分
如果不是完全对称的几何,把特征处理成对称然后按照对称几何的方法来划分



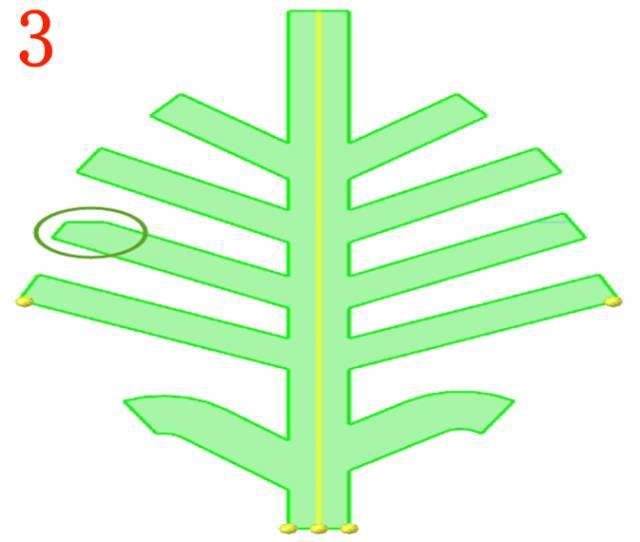
举个例子,图1红圈中的特征可以先划分为图3网格(保留交界面),然后对称至左侧图2并删除多余单元。具体操作如下:

雪花模型看起来很难,实则比较容易构建,下面这种花可是表里如一的困难呢。

蒲公英--复杂模型的分块
蒲公英--复杂模型的分块
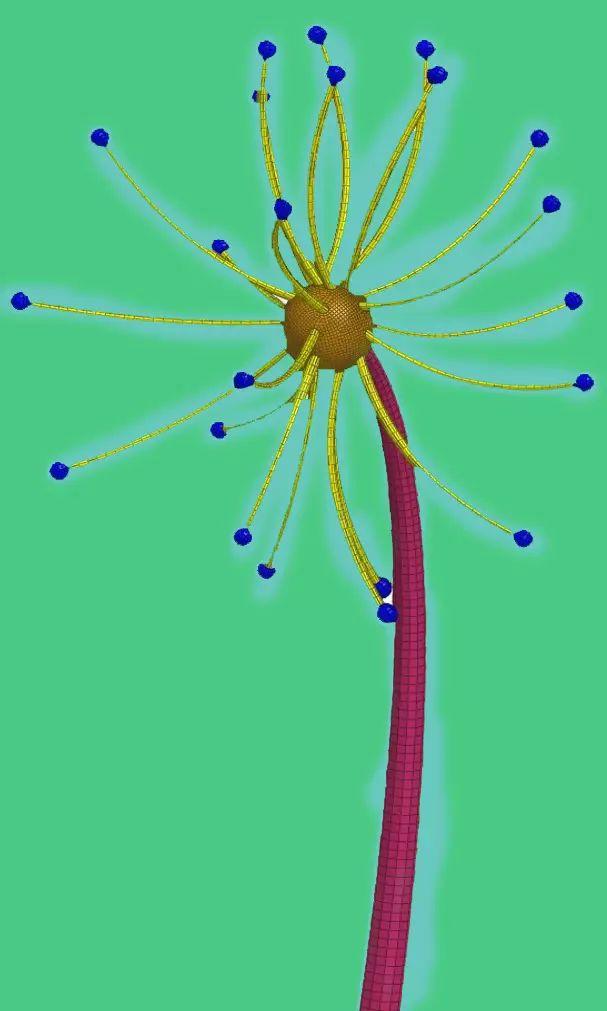
六面体分块属于比较复杂的模型,之后的推送中我们会逐步为大家讲解,在这里先以蒲公英的例子开头,探索六面体分块中的通用原则。
从蒲公英的模型很容易看出所有的“枝条”都是从中间的小球“长出来”的,所以,中间的小球是我们网格划分的起点,而末端的小球由于要旋转360度,用solidmap的方法不容易处理,我们直接旋转2D单元就可以了。
吃饱喝足,也欣赏了风景,你是不是也想自己动手尝试一下呢?利用周末时间,赶紧学起来吧~