【CFD专栏】NanoFluidX：新一代的SPH流体动力学仿真

1月前浏览1752

本文摘要（由AI生成）：

nanoFluidX是一款基于光顺粒子法(SPH)的流体动力学仿真工具，用于预测在复杂几何体中伴随着复杂机械运动的流动情况，如转轴与齿轮传动系统内部的油量分布及各转动部件的扭矩。nanoFluidX的优势体现在简化的前处理、GPU运算带来的优越加速性能、高密度比多相流和刚体运动。SPH与欧拉法的本质区别在于描述物体运动方式的差异，前者为拉格朗日法，后者为欧拉法。SPH求解器采用显式算法，与隐式最大的区别在于求解时间往往非常漫长，因此在建模时要极其注意。SPH方法擅长求解变化剧烈的自由液面的问题，如油箱晃动。SPH最吸引人的地方或许就是“无网格”的概念，摒弃了传统方法中繁琐而冗长的网格划分过程，用粒子取代了网格，使得原本不能解决的问题成为了可能。nanoFuidX的主要工业应用包括传动系统旋转齿轮、曲轴连杆的甩油形态及扭矩预测，加速度突变导致的水箱或油箱晃动等。

大家好呀，今天又是科学的星期五，大家是不是都已经做好了周末的放松计划了呢，但周末也要补充新的知识呢~

我们推出了一个新的栏目为大家讲述CFD的相关小知识，快点看过来吧~

你是否总被冗长而繁琐的CFD前处理所困扰，幻想着不用画网格就能做CFD分析？

nanoFluidX让这种幻想成为可能！

现在就开始我们的第一课吧。

作为Altair的合作伙伴，德国FluiDyn公司在今年发布了全新产品nanoFluidX，提供了一种全新的CFD解决方案。nanoFluidX是一款基于光顺粒子法（Smoothed Particle Hydrodynamics，简称SPH）的流体动力学仿真工具，用于预测在复杂几何体中伴随着复杂机械运动的流动情况，比如转轴与齿轮传动系统内部的油量分布及各转动部件的扭矩。基于粒子计算的特性允许高效地处理具有大变形的流动，例如晃动、掺混的多相流、通过复杂几何的快速流动。

nanoFluidX的优势体现在以下四点：

简化的前处理：

使用无网格算法模拟复杂流动，不再需要传统意义下的网格，只需导入几何并在计算域内生成粒子，大大降低了前处理过程中的手动操作。

GPU运算带来的优越加速性能：

作为NVIDIA ELITE解决方案的供应商，nanoFluidX团队在代码性能优化上极具竞争优势，相比于传统的CPU计算，GPU的计算性能有显著的提高，也更有利于能源及硬件成本和的节约。例如，针对一个转速为上千RPM的齿轮仿真，传统的有限体积法求解器可能需要几周的计算时间，而nanoFluidX可将整个计算周期缩短至几天。

高密度比多相流：

基于SPH的求解器更容易处理高密度比的多相流问题（例如水-空气），流体界面是该方法自然得到的副产品，并不需要采用额外的分界面重构算法（如界面追踪法或界面捕捉法），因此大幅度提高了计算效率。

刚体运动：

nanoFluidX允许通过输入文件预定义刚体的运动轨迹，如行星齿轮运动，从而研究刚体与周围流场的相互作用；同时支持流体作用下的非预设的六自由度刚体运动。

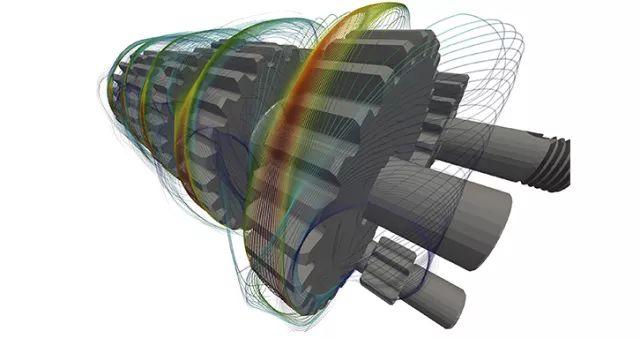
齿轮对在2500RPM转速下的甩油形态

第一次接触基于SPH算法的求解器，通常会有以下这些疑问：SPH和传统的CFD求解器究竟有什么不同？SPH的优势是什么？能解决哪些问题？

接下来我们就来回答一下这些常见的问题吧~要注意看哦~

SPH的全称是Smoothed Particle Hydrodynamics，即光顺粒子法。

这种算法最早是为了研究天体物理而诞生的，后来其应用范围渐渐地被拓展到固体力学和流体力学中。值得一提的是，SPH方法在流体力学中的应用理论及常见模型其实早就已经建立起来了，并不属于新鲜事物，但直到最近几年才出现了商业软件（如NanoFluidX），主要是因为之前受制于硬件无法满足庞大的计算规模这一点。而这些年硬件技术的突飞猛进，正好为推广SPH方法在流体力学中的应用提供了契机。

说到SPH与传统CFD的区别，不得不提一下描述物体运动的两种方式：拉格朗日法和欧拉法。传统CFD求解器在求解纳维斯托克斯方程时采用的是欧拉法，即记录空间坐标上的每个点所对应质点的编号，函数关系中的自变量为空间坐标；而SPH方法采用的拉格朗日法则是通过描述每一个质点在不同时刻的位置来表述整个质点系的位置，即函数关系中的自变量是物质坐标。这就是SPH与传统CFD的本质区别。

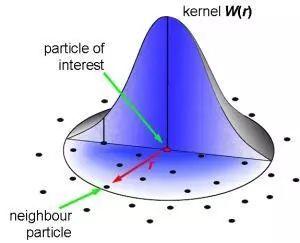
在SPH中要引入一个全新的概念：核函数（Kernel Function），也被称作Smoothing Function或者Broadening Function，其本质都是在描述某一质点的性质及运动状态时给定一个范围（如图），即需要通过该粒子（particle of interest）周围的多少个相邻粒子（neighbor particle）来有效地描述该粒子的情况。其中，SPH粒子可以理解为随流场运动、携带着流体的某些属性（质量、组分浓度等）的离散单元。从数学的角度来说，核函数通常是径向对称的函数，截面类似高斯分布，但是有明确的边界。核函数是流场中流体属性插值计算的重要依据，其形式并不是单一的，比如NanoFluidX中采用的是五次样条核（Quintic spline kernel）。

什么是核函数？

至此，我们提到了SPH与传统CFD之间的本质差别是描述物体运动方式的差异，前者为拉格朗日法，后者为欧拉法。另外，我们也引入了SPH算法中独有的核函数（Kernel Function）的概念。其实说到两者的不同点，还需要提到我们经常听到的“显式”和“隐式”的说法。

通常意义上说，显式和隐式是两类不同的求解方法，可以理解为两者的数学出发点是不同的。传统的CFD求解器采用隐式的数值算法，通常为牛顿迭代法，空间差分的数值格式与时间无关；对于非定常的问题则需要在每一个时间步内迭代收敛后再采用时间格式（如Runge-Kutta时间推进方法）进行瞬态求解。而SPH求解器采用的显式算法，则是对时间进行差分，最小时间步取决于最小单元的尺寸，与隐式最大的区别在于以下三点：所有的求解都是瞬态的、非定常的；不存在迭代收敛的问题；求解时间往往非常漫长，因此在建模时要极其注意。

既然SPH在计算时间上不占优势，那为什么在CFD领域越来越受欢迎了呢？这当然得益于SPH算法中天然存在的一些优势，使得原本用传统CFD方法很难解决或不能解决的问题变得迎刃而解。

在SPH中，每一个颗粒代表着求解主控方程的数值计算中所需要的离散点。这些颗粒随着局部流场一起运动，相当于观察者的视角不固定，而是跟随流场一起移动。这个特质反映到数学方程中，即NS方程中的对流项被自然地剔除了，只剩下了相对容易求解的扩散项。这也使得离散化的过程具有极佳的适应能力，说得通俗点，即能适应极其复杂的计算域，比如那些从初始状态到最终状态计算域变化十分明显的情况。所以SPH方法被普遍认为擅长求解变化剧烈的自由液面的问题，比如油箱晃动。另外两个比较常见的例子就是溃坝和雪崩。

SPH最吸引人地方或许就是“无网格”的概念了。摒弃了传统方法中繁琐而冗长的网格划分过程，用粒子取代了网格，其实不仅仅有助于解放劳动力，也使得原本不能解决的问题成为了可能。由于没有必要在整个计算域内布满流体粒子，这样就能解决那些初始流体域和最终流体域差别很大的问题，比如注油、灌水的过程模拟；喷水、淋水试验等。

在SPH算法中，不同属性的粒子在前处理中就被标记了不同的编号，这样就使得多相流的问题能被轻松求解而不需要加入界面追踪或界面捕捉等算法以识别不同相之间的交界面，比如齿轮箱甩油问题中的油和空气的交界面。事实上，NanoFluidX最初的目标领域就是传动系统的润滑，包括甩油形态分布以及转动体扭矩的估算。