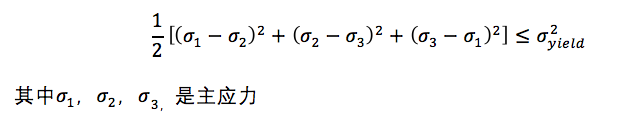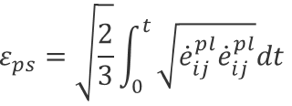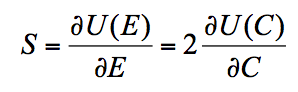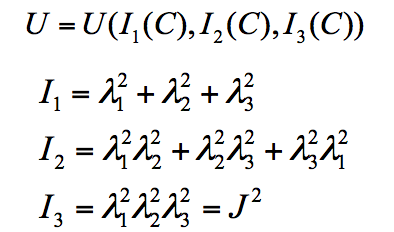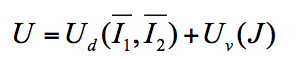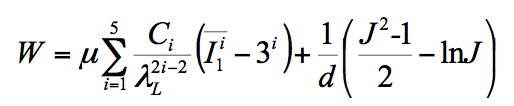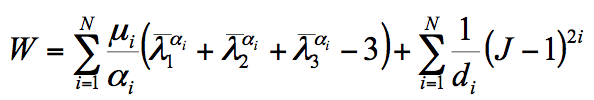【OptiStruct要领】材料非线性模型
本文摘要(由AI生成):
本文主要介绍了OptiStruct中的材料非线性模型,包括弹塑性材料模型和超弹性材料模型。弹塑性材料模型包括屈服准则、流动准则和硬化准则,其中屈服准则采用Mises屈服准则。超弹性材料模型包括多项式模型、统计力学模型和主伸长率模型,其中多项式模型包括Mooney-Rivlin多项式形式、简化的多项式形式、Physical Mooney-Rivlin模型、Neo-Hookean模型和Yeoh模型,统计力学模型为Arruda-Boyce模型,主伸长率模型为Ogden Material模型。
在上一讲中,我们介绍了线弹性体系的三个假设,以及违反小变形假设的几何非线性。这一讲中我们将针对其中另外一条假设,即线弹性体系中材料的应力与应变关系满足虎克定律。但是,众所周知,一般工程材料当达到一定的应力状态后,即出现塑性流动,使其应变与应力呈现非线性关系,这称为材料非线性。
那么,材料非线性模型有哪些呢,我们现在开始学习吧~
在OptiStruct中的材料非线性模型包括:弹塑性材料模型以及超弹性材料模型。
首先介绍下OptiStruct中弹塑性材料模型。
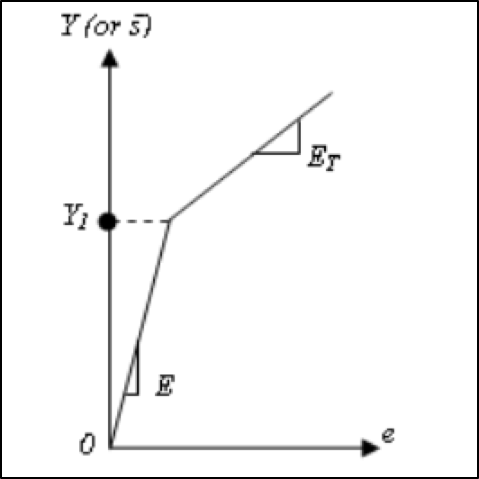
弹塑性材料在加载的初始阶段即弹性阶段,应力—应变关系基本呈线性,斜率即弹性模量。但当应力大于屈服应力时,材料进入塑形,若此后继续加载,应力-应变不呈线性关系,一些情况下仍可近似为线性,但斜率与弹性阶段不同。卸载时,卸载曲线和弹性段曲线斜率相同,但完全卸载后,材料将保留永久的塑形变形。这里由于屈服点和比例极限相差较小,故而OptiStruct中设定两者是同一点。OptiStruct中弹塑性材料的应力应变曲线为:
下面介绍下弹塑性的三要素,即
• 屈服准则
• 流动准则
• 硬化准则
(一) 屈服准则
(一) 屈服准则
屈服准则用于预测材料在一定应力下是处于弹性或者塑性状态,即判别材料是否有塑性应变产生。OptiStruct中用到的屈服准则为Mises屈服准则。Mises屈服准则认为,当材料在复杂应力状态下的形状改变能达到单项拉伸屈服时的形状改变能时,材料开始屈服。Mises屈服准则是除了土壤和脆性材料外典型的屈服准则。
‒ 应力状态在屈服面之内为弹性状态
‒ 应力状态在屈服面上为塑性状态
‒ 应力不会落在屈服面之外
(二) 流动准则
(二) 流动准则
前面提到一般工程材料当达到一定的应力状态后,即出现塑性流动,呈现材料非线性。流动准则是指当材料发生屈服时,塑性应变增量的方向。OptiStruct中流动准则假定塑性势函数与屈服函数一致,塑性变形增量方向总是沿塑性势法线方向。
(三) 硬化准则
(三) 硬化准则
当材料发生屈服卸载后,重新加载,材料将重新屈服,但材料屈服极限提高了,这种现象成为冷作硬化,此时的屈服成为后继屈服。当材料发生硬化后,屈服准则也将发生改变。
OptiStruct中考虑的硬化模型为,各向同性硬化、随动硬化以及混合硬化。在MATS1中控制参数为HR。
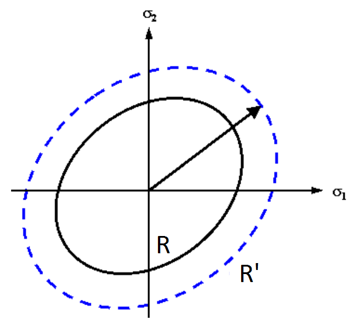
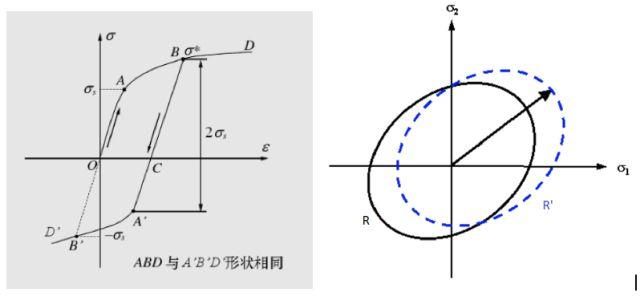
1)各向同性硬化:各向同性硬化即材料硬化后,仍保持各向同性。此时屈服半径变大,屈服中心不变。
但此模型无法反应包辛格效应(实验表明:如果材料从塑形段某点卸载到应力为零点后反向加载,应力在低于初始屈服极限时,就开始屈服)。
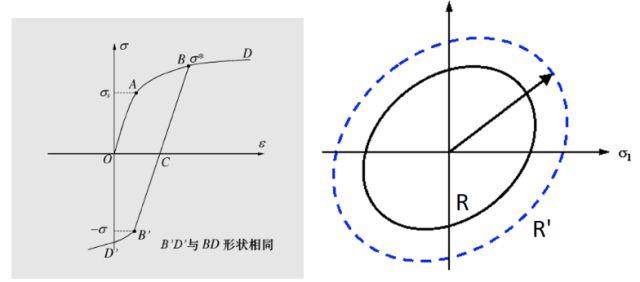
2)随动硬化(运动硬化):材料从塑形段的某点B开始卸载,一旦降低时,材料就开始反向屈服,以后按塑形加载段规律流动(沿与AB段一样的硬化曲线A’B‘流动)。随动强化模型认为后继屈服在塑形变形方向作刚体平行移动。材料在塑性变形方向屈服极限增加了,而在其相反方向屈服极限降低了,因此可反映包辛格效应。此时屈服半径不变,屈服中心移动。
3)混合硬化:为了适应材料的一般硬化特性,同时考虑各向同性硬化以及随动硬化。混合硬化准则中,将塑性应变增量分为两部分即与各向同性硬化相关的塑性应变增量以及和随动硬化相关的塑性应变增量。OptiStruct中默认由30%随动强化和70%各向同性强化构成,当然因子可以通过MATS1材料参数中的HR进行调节。随动强化的因子为HR,各向同性强化的因子为1-HR。此时屈服半径及屈服中心都在变化。
需要注意的是随动硬化和混合硬化仅对实体模型有效。
(四) 增量/全量分析
(四) 增量/全量分析
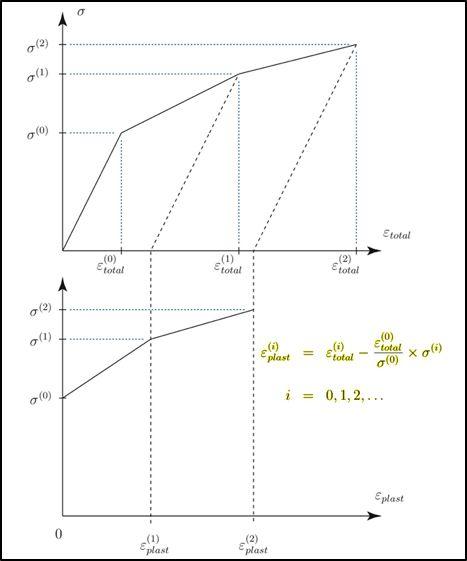
在进行弹塑性分析时,我们选择进行增量/全量的有限元分析方法。全量分析应变包括弹性和塑性应变,而增量分析中应变仅为塑性应变部分。在OptiStruct中,我们可以通过参数MATS1—TYPSTRN来进行控制。那么对应不同的分析方法,应力应变曲线表格的输入MATS1-TID也是不一样的。
➡全量分析(TYPSTRN=0)应力应变曲线TABLES1输入:
起点:(X1 = 0, Y1 = 0);第二点(X2, Y2)=初始屈服点,且斜率=弹性模量(E)
➡增量分析(TYPSTRN=1)应力应变曲线TABLES1输入:
起点:(X1=0, Y1 )
(具体卡片关键字详见HWSOLVER HELP—MATS1)
(五) 输出设置
(五) 输出设置
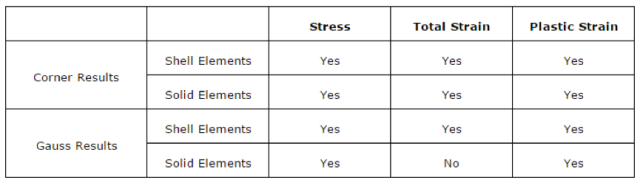
OptiStruct中的弹塑性分析可以在积分点、高斯点、角点输出塑性应变、应力。
等效塑性应变
只要有应变输出要求,都会输出等效塑性应变
塑性应变分量
STRAIN(PLASTIC)=YES
节点塑性应变的输出
GPSTRAIN(PLASTIC) = YES
等效塑性应力
STRESS(VON)=YES
但是需要注意一些限制
➡只能输出实体单元的节点塑性应变
➡只支持静力分析
➡只能输出到H3D文件
这里需要注意的是,如果加载过程是承接上一步加载,而不是若干个独立的工况,则需要在GLOBAL_CASE_CONTROL这里设置CNTNLSUB,YES
讲解之后,就让我们来看个简单的例子吧~
这是一个材料拉伸实验的例子。如下图所示试件,一端固支,一端收+x方向拉力。考察其塑性应变。
1
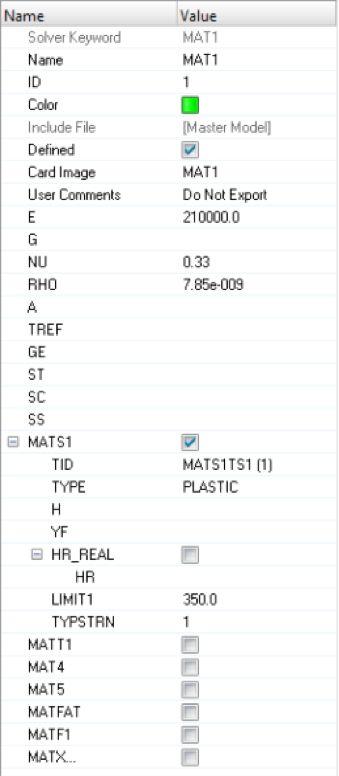
材料模型的定义
2
这里用到增量分析方法
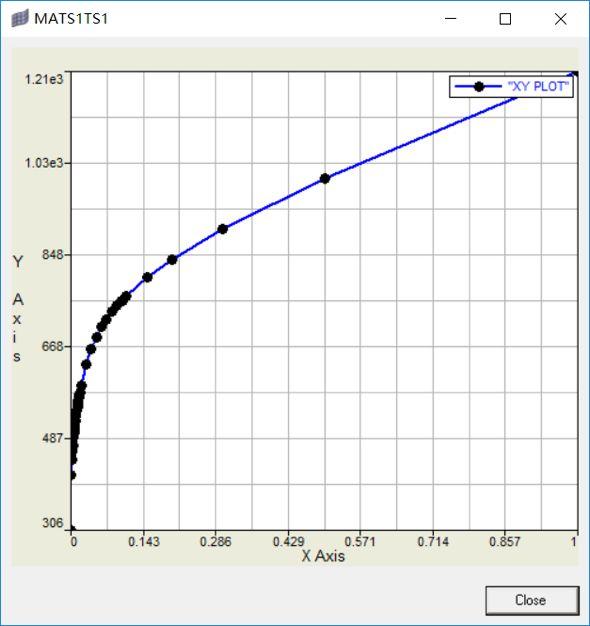
其中应力应变曲线由TABLES1表格输入。起点为屈服点。
3
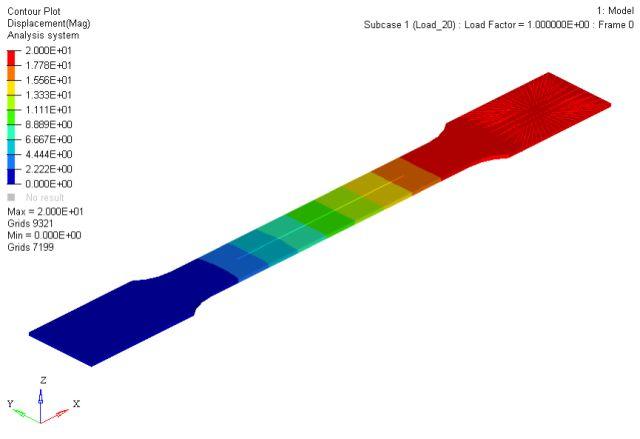
结果输出
位移:
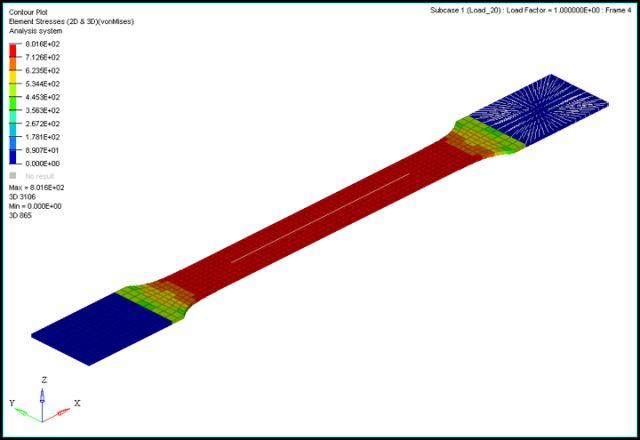
应力:
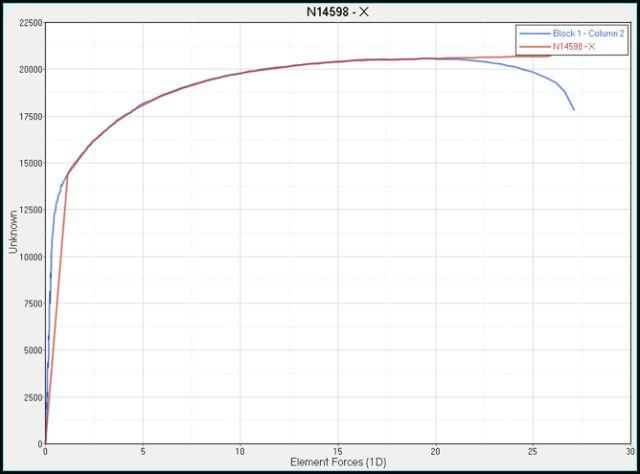
以及spc force的实验及仿真曲线的对比。蓝色为实验曲线,红色为仿真结果。
除了弹塑性材料本构外,OptiStruct还可以定义超弹性材料。
超弹性材料实质就是一种非线性弹性材料,在较大的变形下也保持弹性特性。超弹性材料的行为比金属材料行为要复杂得多,该模型可用于分析各种橡胶类、泡沫类材料,这种材料能够承受大应变和大位移,但体积改变极小(超弹性材料一般为不可压或近似不可压缩材料),比如吹气球,又如橡胶按钮受压缩等,这种分析需用到大应变理论。
超弹性材料应力应变关系通过应变能密度函数来描述
S = second Piola_Kirchhoff stress tensor
E = Lagrangian strain tensor
U= strain energy function per unit undeformed volume
C = right Cauchy-Green deformation tensor
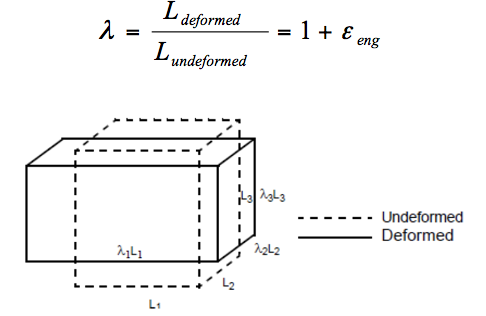
在实际应用中应变能密度一般采用体积应变及主方向上的伸长率来描述
让我们先看下超弹性中的几个术语吧~
➡伸长率:变形后长度除以变形前长度
➡体积应变:变形后体积除以变形前体积;对于不可压缩的超弹性材料=1
➡应变能密度函数:应变能密度函数一般通过3个不变量来描述,其中3个不变量又可用3个主方向的伸长率来表示
对于不可压缩超弹性材料,其应变能密度可通过偏应变张量不变量及体积应变来表示。
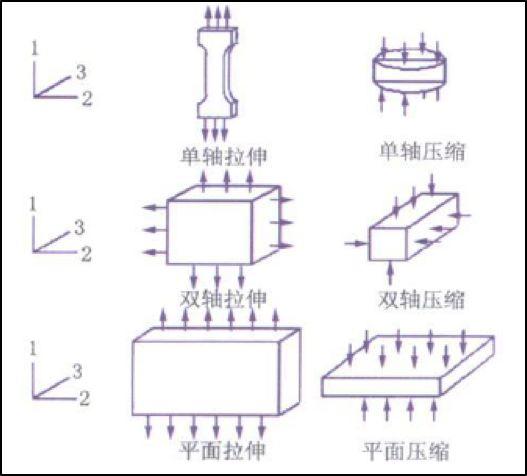
为了完整描述超弹性材料模型,理论上需要6种纯应变状态的力学实验:单轴拉伸、单轴压缩、等双轴压缩、等双轴拉伸、平面拉伸、平面压缩。
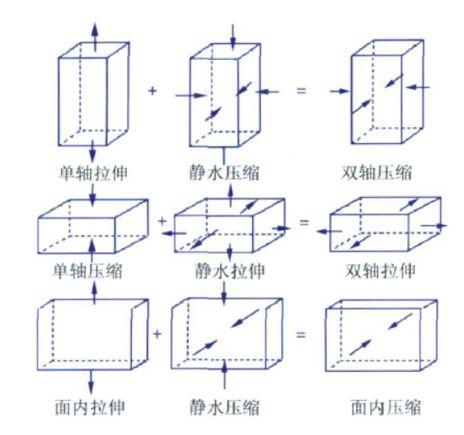
由于超弹性材料的不可压缩特性,有三组实验理论上存在应力状态等效关系。
因此,超弹性材料的3中基本力学实验为:单轴拉伸(等效的等双轴压缩)、单轴压缩(或等效的等双轴拉伸)、剪切(平面拉伸或压缩)。
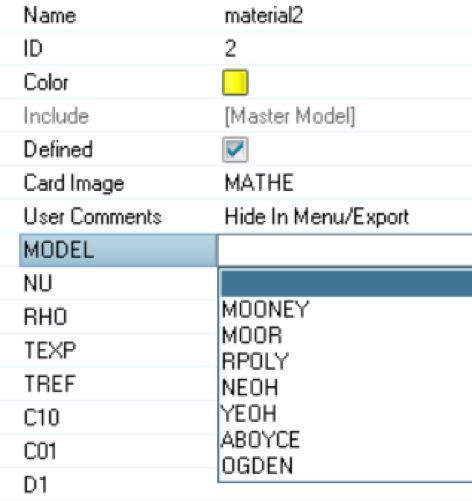
在OptiStruct中,超弹性材料模型有:Mooney-Rivlin多项式形式(MOONEY),简化的多项式形式(RPOLY),Physical Mooney-Rivlin 模型(MOOR), Neo-Hookean 模型(NEOH),Yeoh 模型(YEOH),Arruda-Boyce 模型(Model=ABOYCE),Ogden Material 模型(Model=OGDEN)
1)基于第一和第二应变不变量的多项式模型
MOONEY,RPOLY,MOOR,NEOH,YEOH
(W:应变能密度不同的模型,应变能密度函数不一样,具体可查MATHE卡片comments相关。)
2)基于统计力学的模型
ABOYCE
3)基于主伸长率的模型
OGDEN
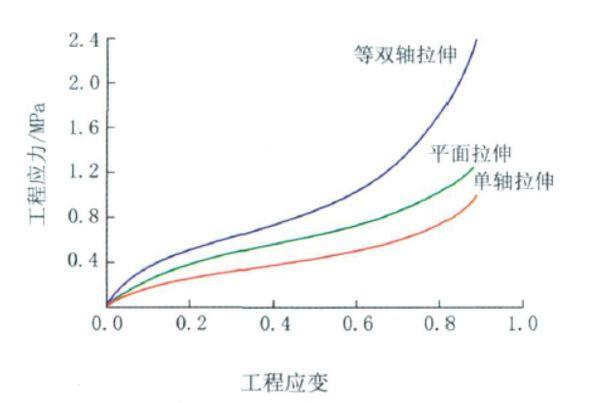
超弹性模型数值—实验结果对比
超弹性模型特点
Neo-Hookean
在小变形下,同实验拟合结果很好
无法模拟后期大变形的刚度陡升段
Mooney-Rivlin
在应变小于100%时,可得到合理的结果
无法模拟后期大变形的刚度陡升段
Yeoh (N=3)
在很大的变形范围内都可得到合理的结果
能模拟后期刚度急剧上升段
很少的实验数据就可得到合理的数值结果,如只有单轴拉伸试验结果
Ogden (N)
建议N取3
可在较大的变形范围内得到较高精度的数值结果
能模拟后期刚度急剧上升
在实验数据不足的情况下不建议使用,如只有单轴拉伸实验结果
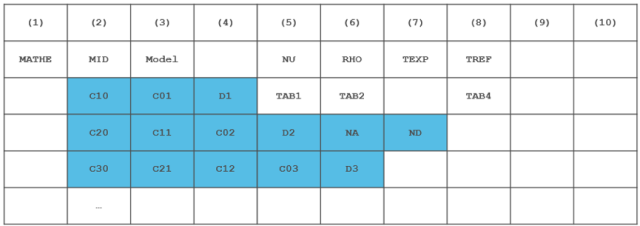
MATHE可通过两种方式定义
MATHE可通过两种方式定义
方法1
直接输入简单载荷下的实验曲线,TAB1单轴拉伸,TAB2等双轴拉伸,TAB4纯剪,TABD体积应变下的压力曲线,OptiStruct会自动拟合多项式参数进行求解。
方法2
直接输入多项式的各个参数
介绍完理论部分,按照国际惯例,接下来就是动手环节啦~
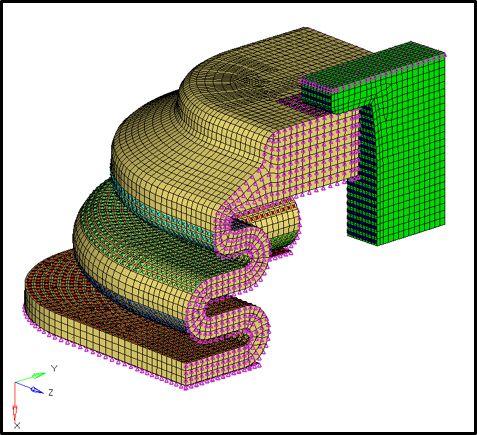
这个模型我们将进行橡胶材料加载卸载的变形分析,模型对象如下图所示
步骤 1
进行材料模型的设定
我们要用到的橡胶材料就是刚刚介绍的超弹性模型。
这里我们直接通过设定多项式系数参数进行来拟合该模型。
步骤 1
进行材料模型的设定
我们要用到的橡胶材料就是刚刚介绍的超弹性模型。
这里我们直接通过设定多项式系数参数进行来拟合该模型。
步骤 2
创建新的单元属性
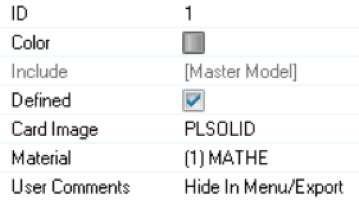
对于超弹性单元,OptiStruct中的属性对应的是PLSOLID。
其他部分材料皆为钢。
步骤 2
创建新的单元属性
对于超弹性单元,OptiStruct中的属性对应的是PLSOLID。
其他部分材料皆为钢。
步骤 3
载荷边界及接触对的建立
步骤 3
载荷边界及接触对的建立
步骤 4
参数及输出(CONTROL CARD)
对于橡胶型材料,受载荷作用下尽管材料仍处于弹性状态,但是可能出现很大的应变,,这时平衡方程应当建立在变形后的位形上,以考虑变形对平衡方程的影响,也就是说在这里,我们还需要引入几何非线性。
如果你有加载和卸载两个工况,别忘了
最后看下变形过程中的位移变化
以及加载工况下的应变
步骤 4
参数及输出(CONTROL CARD)
对于橡胶型材料,受载荷作用下尽管材料仍处于弹性状态,但是可能出现很大的应变,,这时平衡方程应当建立在变形后的位形上,以考虑变形对平衡方程的影响,也就是说在这里,我们还需要引入几何非线性。
如果你有加载和卸载两个工况,别忘了
最后看下变形过程中的位移变化
以及加载工况下的应变