【ATC优秀论文4】基于OptiStruct的电动汽车电池包振动疲劳分析
本文摘要(由AI生成):
本文主要介绍了基于OptiStruct的电动汽车电池包振动疲劳分析方法。首先,通过Hypermesh建立电池包的结构有限元模型,并进行模态频响分析。然后,基于频域法分析其在随机振动环境下的响应,获得应力功率谱密度。最后使用OptiStruct对电池包进行随机振动疲劳分析。分析结果表明,电池包的结构可以满足国标中(GB/T31467)随机振动试验的要求。基于OptiStruct的随机振动疲劳分析方法成功指导了电池包的开发设计。
《基于OptiStruct的电动汽车电池包振动疲劳分析》
李西顺
中能绿驰成都汽车科技有限公司
摘要
摘要
电池包的疲劳耐久性能是电动汽车开发时需要重点考察的指标之一。首先,通过Hypermesh建立电池包的结构有限元模型,并进行模态频响分析。然后,基于频域法分析其在随机振动环境下的响应,获得应力功率谱密度。最后使用OptiStruct对电池包进行随机振动疲劳分析。分析结果表明,电池包的结构可以满足国标中(GB/T31467)随机振动试验的要求。基于OptiStruct的随机振动疲劳分析方法成功指导了电池包的开发设计。
1.
>>>前言<<<

近年来,节能减排和发展清洁源成为国家重要战略,电动汽车成为最重要的选择之一。电动汽车的需求及销售量也越来越大[1]。电池包是电动汽车的核心部件之一,作为电池组的载体,对电池组的安全工作和防护起着关键的作用,其安全性能是电动汽车安全性能的重中之重[2]。由于路面的不平度,电池包在车辆行驶过程中会发生随机振动,因此,研究随机振动对电池包的疲劳寿命影响具有重要意义。
结构在随机振动载荷作用下容易出现疲劳破坏,分析方法有时域和频域两种方法,时域法中经典的雨流循环计数方法被认为是最准确的方法,但获取和处理长时间的应力时域信号较为困难,因此,在工程实践中应用受到很大限制[3]。随机振动学里通常用功率谱密度(Power Spectral Density, PSD)来描述随机载荷信号,主要优点是能够描述振动频率,了解振动中的有效频率分量。因此对随机振动的应力分析,主要使用频域的谱分析法,从应力功率谱密度出发,得到应力幅值的概率密度函数,进而进行随机振动疲劳分析[4]。
本文采用有限元方法并基于频域法,对随机振动试验的电池包结构进行疲劳寿命分析。文中给出了振动疲劳寿命分析的主要仿真流程,即首先对电池包进行频响分析,然后结合国标(GB/T 31467.3)规定的PSD载荷谱进行随机振动响应分析,进一步地,再进行随机振动疲劳寿命分析。
2.
>>>理论基础<<<

2.1 | 振动疲劳 |
随机振动是指任一给定时刻的瞬时值不能预先确定的机械振动,无法用确定性函数而须用概率统计方法定量描述其运动规律的振动。振动耐久理论研究兴起于20世纪80年代末。很多学者专家为此做了很多研究,其中Sanliturk等利用频率响应传递函数的方法预测疲劳寿命,该方法除了考虑了结构本身弹性又考虑了结构阻尼以及惯性对于疲劳寿命的影响[5],而Bishop则利用功率谱密度函数计算出疲劳损伤计算[6],但该方法计算量很大,很少被实际应用。1985 年Dirlik在以往经验基础上然后结合Monte Carlo技术进行了全面计算机模拟[7],精度基本和Bishop方法精度相当。
Dirlik的数学表达式为[7]:
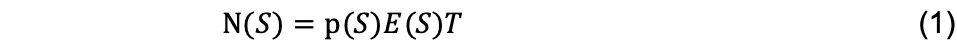
式中:p(S)——应力幅值的概率密度函数.
2.2 | 功率谱密度PSD |
频域内的主要优点是能够描述振动频率,了解振动中的有效频率分量,在频域中,PSD 是一个最基本的量,通过谱分析可以了解随机振动的频率成分[8]。
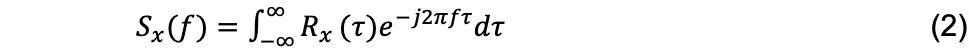
式中:
Sx (f)——自功率谱密度函数
f——频率
Rx (τ)——自相关函数
Sx (f) 表征着能量按频率分布的情况。
单边功率谱密度定义为:
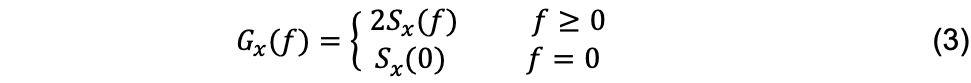
2.3 | 功率谱密度惯性矩 |
结构激励信号的功率谱密度为W(f),则应力功率谱密度为:

其中,H(f)为应力频响函数。
在时域中,常用一些统计参数来描述一个随机应力应变时间历程中1s的样本,如图1所示,图中E[0]为样本中自下而上穿越均值的次数,E[P]为样本中出现峰值的次数。
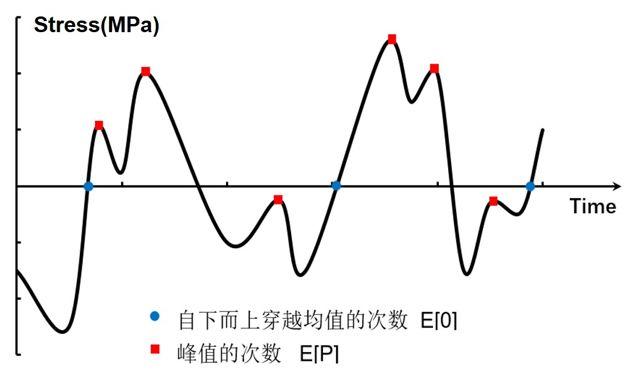
图1 应力时间历程图
研究发现这些统计参量可以通过功率谱密度函数的n阶惯性矩mn换算得到。惯性矩即为功率谱密度函数曲线下包括的面积。如图2所示。

图2 PSD的惯性矩的计算
应力功率谱密度的第n阶惯性矩mn为:
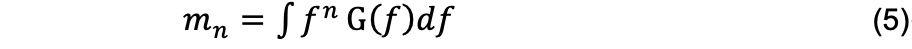
然后,不规则因子由以下的公式进行计算:
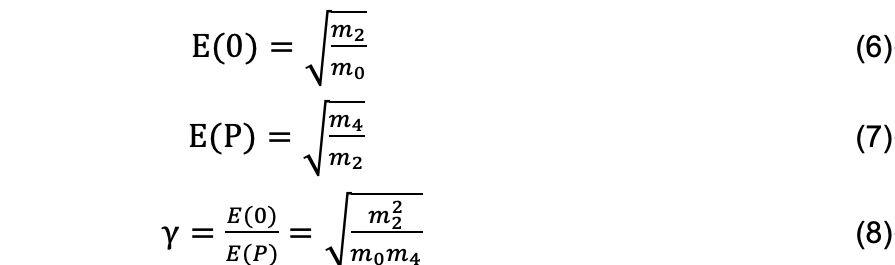
2.4 | 应力幅值的概率密度函数 |
对于DIRLIK方法,应力幅值的概率密度函数,计算公式为[8]:
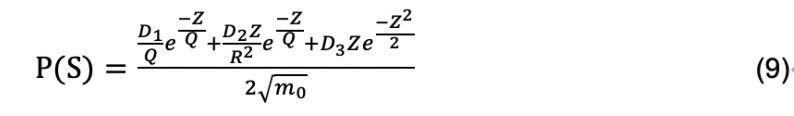
其中,
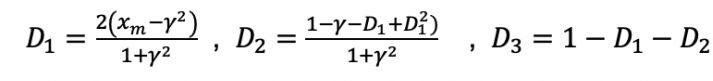

m0, m1, m2, m3——分别为功率谱密度函数的0,1,2,4阶惯性矩;
γ——不规则因子。
3.
>>>电池包振动疲劳分析<<<

3.1 | 振动疲劳分析流程 |
振动疲劳分析的主要分析主要流程如图3所示:

图3 随机振动疲劳分析流程
3.2 | 电池包有限元模型 |
整个电池包模型包括外部壳体,支架和内部电池等。使用Hypermesh软件建立有限元模型,如图4所示,共324242个单元。电池包壳体主要采用壳单元,单元尺寸为5mm;电池连接杆采用beam单元模拟,并与电池、电池夹板固接;焊点采用Rbe2和Cweld两种连接方式进行模拟,对于电池,作为质量点进行模拟。

图4 电池包有限元模型
电池包壳体材料为铝合金材料,材料弹性模量为7.1e+4MPa,密度为2.7e+3kg/m3,泊松比为0.35。
边界条件:电池包安装固定点进行123456固定约束。如图5所示。

图5 电池包固定约束位置
频响分析:利用OptiStruct 模块通过模态法对电池包模型进行频响分析,得到模型每一阶模态在X、Y、Z 三个方向上单位加速度G激励下的传递函数,输出幅值和相位信息。
3.3 | PSD载荷谱 |
国标(GB/T 31467.3)中对电池包及动力电池系统的振动载荷使用加速度PSD谱进行了定义,如图6所示。随机振动响应分析时可直接输入加速度PSD谱作为振动载荷。由于在前期静力分析结果中,Z向加速度的工况下,安装点附近的应力最大,故疲劳分析重点考查Z向加速度载荷谱。

图6 PSD载荷谱
3.4 | S-N曲线 |
最常用的S-N曲线是幂函数 lgS=A+BlgN,其中A、B为材料常数,S为应力,N为寿命。
本次分析所用的材料为的S-N曲线图7所示:
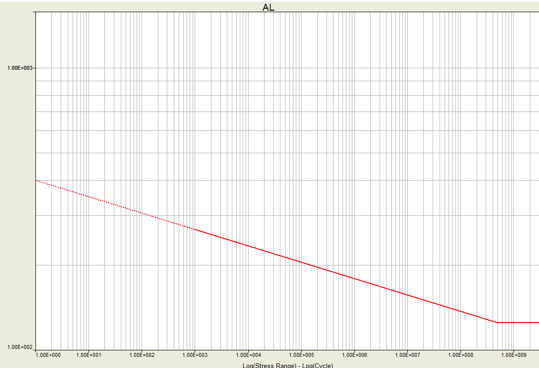
图7 电池包壳体材料的S-N曲线
4.
>>>分析结果<<<

4.1 | 频响分析结果 |
电池包频响分析结果,如图8所示,图中为几个不同位置的加速度响应结果,电池包壳体上响应比较大的几个位置。
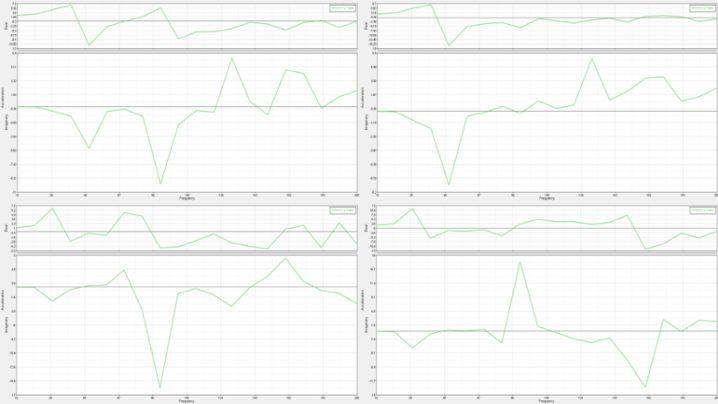
图8 不同位置的频响结果(加速度响应)
4.2 | 随机振动分析结果 |
由OptiStruct计算随机振动分析,获得RMS应力,RMS应力如图9所示。结果与静力学分析结果一致,最大应力位置均出现在安装点附近。故振动疲劳分析重点关注安装点附近区域。
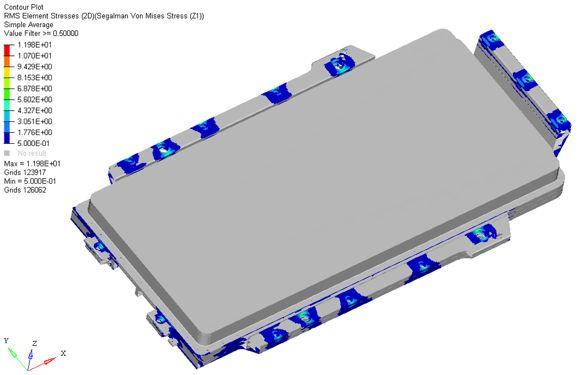
图9 电池包随机振动分析RMS应力结果
4.3 | 振动疲劳分析结果 |
本文直接使用Optistruct计算振动疲劳寿命,国标中要求测试时间为21h,即振动时间为T=7.56e4s。
分析结果如图10所示。结果显示最危险位置发生在安装点附近,寿命结果为1.9e5,因此该电池包结构可满足随机振动条件下的疲劳要求。说明其能够满足多变运行环境和行驶工况下的疲劳寿命要求,保护电池组,保障整车安全性。

图10 电池包随机振动疲劳分析结果
5.
>>>结论<<<

本文介绍了使用OptiStruct软件,基于PSD谱,进行电池包疲劳寿命计算的流程。分析结果与台架试验结果相符,在后续的路试试验中,电池包未出现疲劳断裂现象,说明电池包结构设计合理。这套疲劳分析流程可以在电池包设计阶段有效控制其疲劳寿命,缩短开发周期,降低开发成本,指导开发设计。
OptiStruct作为一款先进的结构分析求解器,具有高精准的求解精度,同时其求解能力仍在不断的完善,比如几何大变形问题,接触非线性,焊点疲劳以及本文中用到的振动疲劳等,为解决实际的工程问题提供了极大的帮助。
参考文献
[1] 李晓华. 新能源汽车技术发展的挑战、机遇和展望[M]. 北京:机械工业出版社,2012.
[2] Kitoh K, Nemoto H. 100 Wh Large size Li-ion batteries and safety tests[J]. Journal of Power Sources, 1999, 81–82(9):887-890.
[3] 董保童,施荣明,朱广荣.随机振动载荷作用下的结构疲劳寿命估算 [J]. 飞机设计. 2001(03):36-41
[4] 刘龙涛,李传日,程祺. 某结构件的随机振动疲劳分析[J].振动与冲击,2013, 32(21).
[5] SANLITURK K Y.Fatigue life prediction using frequency response function[J].Journal of vibration and Acoustics,1992,114(7):381-386.
[6] BISHOP NWM.Vibration fatigue analysis in finite element environment[C]. TheXVI ENCUENTRO ESPANOL DE FRACTURA.Torremolinos,Spain,1999:14-16.
[7] 庄表中,陈乃立. 随机振动的理论及实例分析 [M]. 北京:地震出版社,1985:216-222.
[8] Altair, RADIOSS Reference Manual.




