【ATC优秀论文7】铁道客车模态参数识别及车体支撑刚度研究
本文摘要(由AI生成):
本文主要研究了铁道客车车体模态参数识别及车体支撑刚度变化对模态频率的影响。通过对某型铁道客车车体进行计算与试验对标,发现整备状态下一阶垂弯计算与试验频率均高于标准规定的10Hz,计算误差基本在5%以内,能够满足工程应用要求。同时,结构车体在弹性支撑作用下的各阶模态频率略大于自由模态频率,且随着支撑刚度的增大各阶模态频率呈增大趋势。建议今后模态试验用于结构车体弹性支撑的刚体频率在3Hz~5Hz范围内选取,同时建议对于铁道车辆模态仿真计算可直接计算车体的自由模态。
《铁道客车模态参数识别及车体支撑刚度研究》
徐聪,李家宝
中车青岛四方车辆研究所有限公司
摘要
摘要
基于有限元和试验模态分析技术对某型铁道客车车体进行了计算与试验对标,同时研究了结构车体支撑刚度变化对模态频率影响的变化特性。研究结果:该研究对象整备状态下一阶垂弯计算与试验频率均高于标准规定的10Hz,能够满足标准的相关要求,计算与试验误差基本都在5%以内,其计算精度能够满足工程应用要求;结构车体在弹性支撑作用下的各阶模态频率略大于自由模态频率,且随着支撑刚度的增大各阶模态频率呈增大趋势;建议今后模态试验用于结构车体弹性支撑的刚体频率在3Hz~5Hz范围内选取,同时建议对于铁道车辆模态仿真计算可直接计算车体的自由模态。
随着铁道客车运营速度的不断提高,人们对于车辆系统的安全性及舒适性要求不断提升,用于描述车辆系统固有振动特性的模态参数也逐渐备受关注。目前,行业内所采用的有限元模态识别、试验室模态识别、试验室滚振台模态识别以及线路试运营模态识别等一系列措施,均体现了模态参数指标在现代轨道车辆系统设计过程中的重要性。
与此同时各个国家对于车辆系统的模态参数识别都予以高度重视,分别对模态参数制定了相应的指标。其中,德国要求整备状态下车体的最低自振频率不允许低于10 Hz,弯曲振动频率和转向架点头及浮沉振动频率比值不得低于1.4倍;瑞典要求车辆系统各部件间的固有频率应相差3.0 Hz以上;法国国营铁路要求转向架的振动频率不与车体弯曲振动频率相耦合,分隔范围希望在1.5 Hz以上;意大利和日本的高速车辆要求弯曲共振频率不低于10Hz[1]。我国通过引进国外经验在TB/T 3115-2005中也明确规定:在整备条件下,车体一阶弯曲自振频率与转向架的点头和沉浮自振频率的比值应大于1.4倍。在没有检测转向架的点头和沉浮自振频率情况下,整备状态车体一阶弯曲自振频率应不低于10Hz [2]。
由于目前仿真分析往往都是基于车体自由状态下的模态分析,而车体的试验频率一般都是在弹性体支撑作用下测得,因此,有必要对其进行对比研究。本文以某型铁道客车为研究对象,依据TB/T 3115-2005标准,分别采用有限元和试验的方法进行模态参数分析,并通过计算与试验的对标,研究车体支撑刚度对模态频率的影响。
基本理论
基本理论
有限元模态仿真分析
通常采用有限元求解系统的固有频率和模态振型,主要是求解结构无阻尼和自由状态下系统的动力特性方程[3]:

式中,

和a(t) 分别为系统节点加速度向量和节点位移向量,M和K分别为系统的质量矩阵和刚度矩阵。
上式的解可以假设为以下形式:

式中,

为n阶向量,ω为向量 的振动频率,t是时间变量,t0是由初始条件确定的时间常数。
将式(2)带入式(1)可得广义特征值求解方程:

求解式(3)可确定

和ω,得到n个特征解:
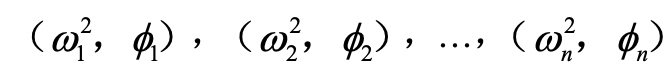
其中,ω1,ω2,…,ωn代表系统的n个固有频率,且0≤ω1<ω2<…<ωn。特征向量

代表系统的n个固有振型。
试验模态分析
试验模态分析
试验模态分析是利用振动激励与响应测试、数字信号处理技术以及参数识别方法来求得系统模态参数进而确定结构动态特性的现代分析技术[4]。
目前,LMS Test.Lab推出了LMS PolyMax(最小二乘复频域法),采用了一种新的频域估计技术PolyMax,该方法在强阻尼、密集模态情况下,可获得清晰的稳态图,从而实现物理模态定阶[1]。
PolyMax法要求首先计算各响应点对激励力的频响函数,然后把各测点的全部频响函数按幅值求和,使峰值信息集中在系统综合频响函数之和中,形成模态参数识别的稳态图。在模态参数识别的稳态图“稳定极点”处选择极点,对选定的极点进行模态向量估计,最终得到结构的模态频率、振型、阻尼比。
车体模态仿真计算
车体模态仿真计算
本文选用的某型铁道客车的车体结构为全碳钢焊接结构,其结构车质量约为19.5t,整备车体车身质量约为47.6t。车体钢结构的材料属性见表1所示。

车体有限元建模简介
车体有限元建模简介
本文计算采用通用有限元软件Altair HyperMesh建立了结构车和整备车有限元模型,求解器为Altair OptiStruct。车体钢结构采用壳单元模拟,单元大小约为20mm,结构车有限元模型见图1,单元数量约168.5万。

图1 结构车体有限元模型
整备车体模型在结构车模型的基础上增加了对司机室布置、环控系统、设备系统、内装系统、电气系统以及制动系统的模拟,各系统根据其设计质量分布分别采用质量点CONM2单元简化处理,其中,车门、车窗等连接刚度相对较小的部件采用RBE3与车体耦合约束,对于车下刚性吊挂设备采用RBE2与车体耦合约束。整备车体单元数量约184.3万,有限元模型见图2。

图2 整备车体有限元模型
车体模态仿真计算结果
车体模态仿真计算结果
采用有限元模态分析方法获取结构车和整备车车体自由状态下的低阶典型模态,主要包括一阶菱形、一阶呼吸、一阶横弯、一阶垂弯和一阶扭转。车体各阶模态计算结果见表2,各阶的振型图见图3、图4。
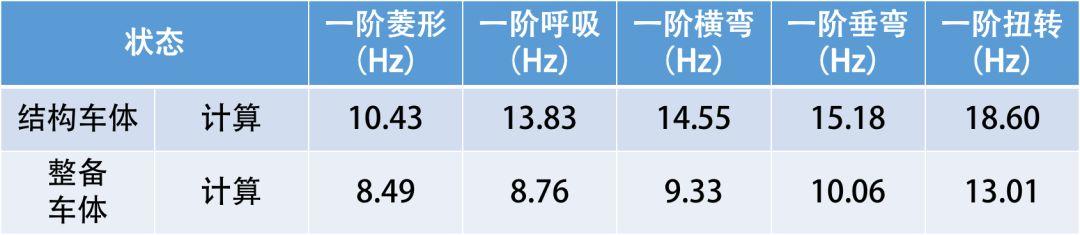
表2 结构车和整备车车体各阶频率统计结果(计算)
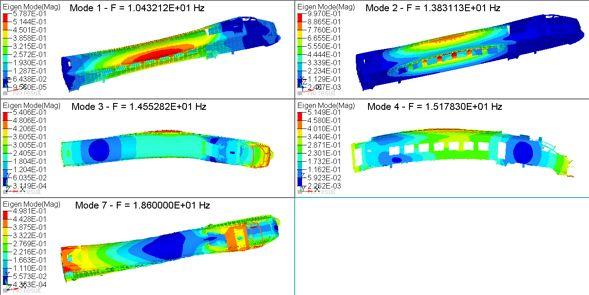
图3 结构车体低阶典型振型图
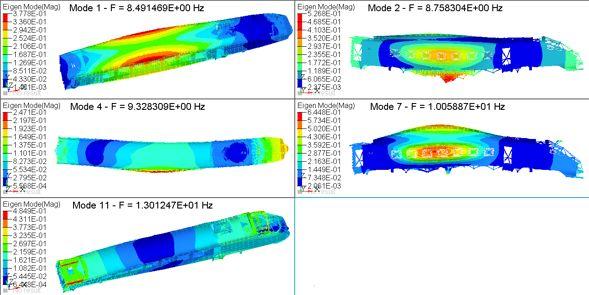
图4 整备车体低阶典型振型图
车体模态试验
车体模态试验
车体模态试验简介
车体模态试验简介
本次试验的结构车体采用橡胶堆支撑,整备车体为原装转向架及空气弹簧支撑,其设备齐全,空气弹簧充气压力符合整备车辆技术要求。被试车体见图5、图6。

图5 结构车被试车体

图6 整备车被试车体
试验设备主要包括动态数据采集系统(1套)、加速度传感器(16个)、力传感器(4个)、模态激振器(4套)。模态试验系统组成示意图,见图7。
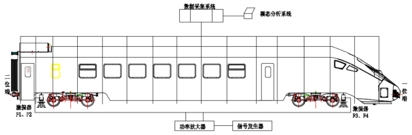
图7 模态试验系统组成示意图
本次试验依据TB/T 3115-2005标准,根据该铁道客车车体的结构特点,沿该车车体长度方向基本均匀布设16个断面,每个断面共14个测点,每个测点测试垂向和横向两个方向加速度。试验中采用4台模态激振器作为车体模态试验的激振源,激励点位于车体底架的两端刚度较大处。试验采用2Hz~40Hz猝发随机信号进行激励,采样频率为1024Hz。
车体模态试验结果
车体模态试验结果
采用试验模态分析方法获取结构车体和整备车体的低阶典型模态。车体各阶频率的试验结果见表3,各阶振型见图8~图15。
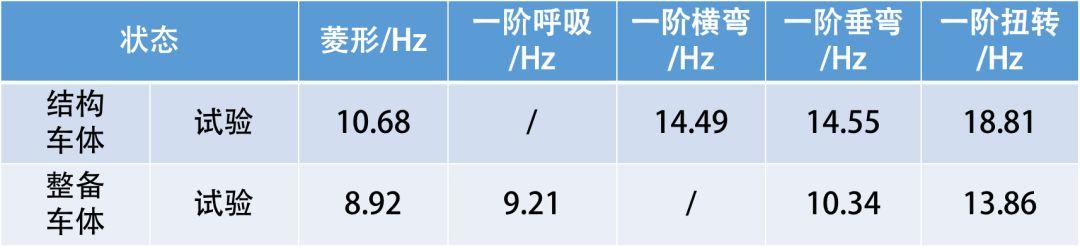
表3 结构车体和整备车体各阶频率统计结果(试验)
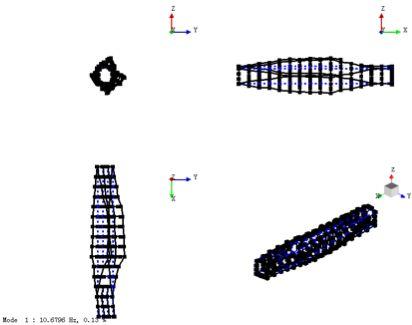
图8 一阶菱形振型图
(结构车体)

图9 一阶横弯振型图
(结构车体)
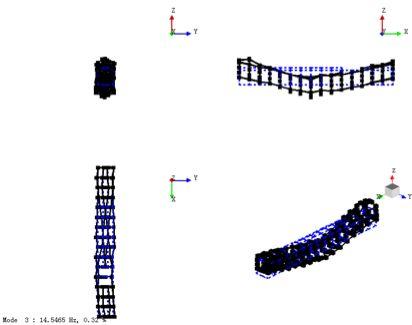
图10 一阶垂弯振型图
(结构车体)
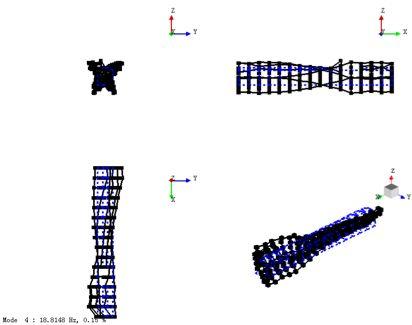
图11 一阶扭转振型图
(结构车体)
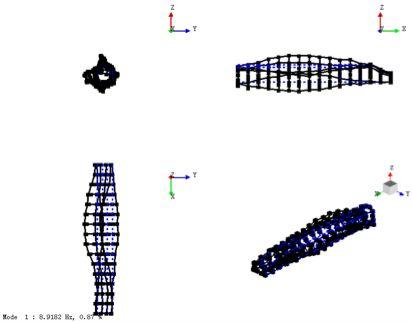
图12 一阶菱形振型图
(整备车体)
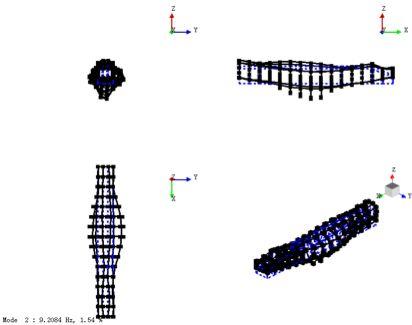
图13 一阶呼吸振型图
(整备车体)
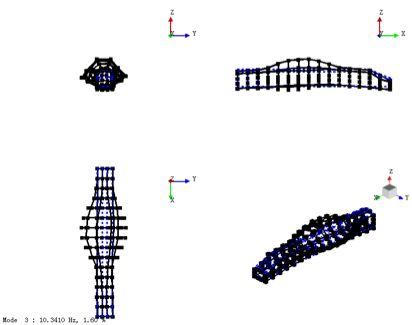
图14 一阶垂弯振型图
(整备车体)
图15 一阶扭转振型图
(整备车体)
车体模态仿真计算与试验对标
车体模态仿真计算与试验对标
本文对结构车体和整备车体低阶典型模态的计算与试验结果进行了对标,对比分析结果见表4。
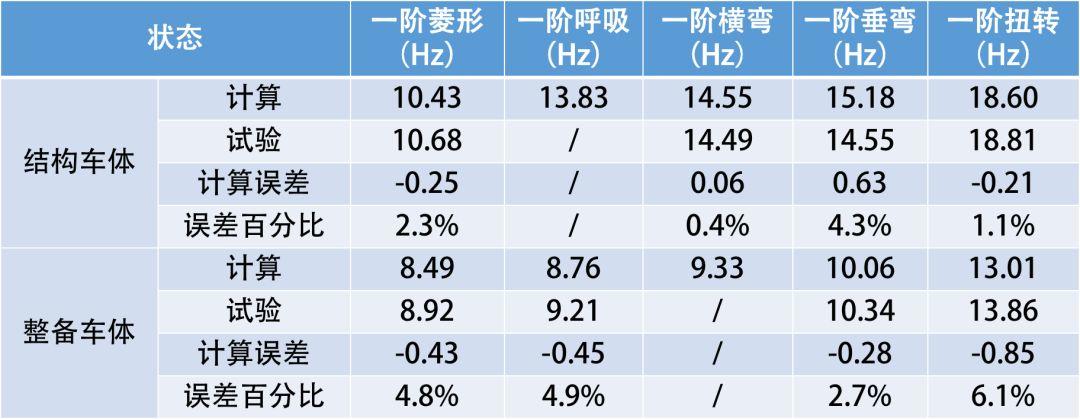
表4 车体模态计算与试验对比分析结果
根据TB/T 3115-2005规定,在整备状态下车体一阶弯曲自振频率应不低于10Hz[2]。由表4可见:整备车体一阶垂弯计算频率为10.06Hz,一阶垂弯试验频率为10.34Hz,且二者振型一致,其一阶垂弯频率均大于标准规定的10Hz,因此,该研究对象整备车体能够满足标准规定的相关要求。
根据计算与试验对比可知:计算误差(除整备车体一阶扭转)均在5%以内,模态振型一致,该计算结果能够满足目前工程应用的仿真精度要求。整备车体一阶扭转的计算误差大于5%,其原因可能是由于有限元对扭转刚度的模拟不足导致。
支撑刚度对结构车体模态影响研究
支撑刚度对结构车体模态影响研究
根据TB/T3115-2005相关要求,整备车体进行模态测试时,车体应采用低刚度的材料(如气囊)支撑在转向架二系悬挂点处,也可以在现车状态下,进行工作模态的测定[2]。其对于结构车体支撑条件未进行明确说明。
通过调研发现,整备车体相关模态试验均在现车状态下完成。因此,本文对于整备车体支撑不予考虑,仅通过仿真分析手段研究结构车体在不同支撑刚度作用下的模态参数变化特性。结构车体在弹性支撑作用下可简化为单自由度弹簧系统,其弹性单元的刚度可由下式计算得出[5]:

式中:k为弹簧刚度,f为刚体频率,m为车体质量。
本文通过设定弹簧系统刚体频率的方法获取弹簧单元的刚度值。结构车体在弹性支撑作用下的刚度设置以及模态计结果见表5,频率变化趋势线见图16。
由表5及图16可见,随着支撑刚度的增大结构车一阶呼吸和一阶横弯频率基本无变化;一阶垂弯频率呈缓慢增长的趋势,最大变化量为0.07Hz;一阶菱形和一阶扭转增长相对较大,其最大变化量分别为0.23Hz、0.45Hz。
综上所述,随着支撑刚度的变化各阶频率变化量级较小,为此,本文定义当频率变化量大于0.1Hz时,支撑刚度会对结构车体模态频率产生影响。由表5可知,刚体频率小于5Hz时各阶弹性体频率变化量能够满足小于0.1Hz要求,同时由安全考虑结构车体落于弹性支撑上不能因位移过大而产生倾覆,建议今后用于结构车体模态试验弹性支撑的刚体频率在3Hz~5Hz范围内选取,同时建议对于铁道车辆模态仿真计算可直接计算车体的自由模态。
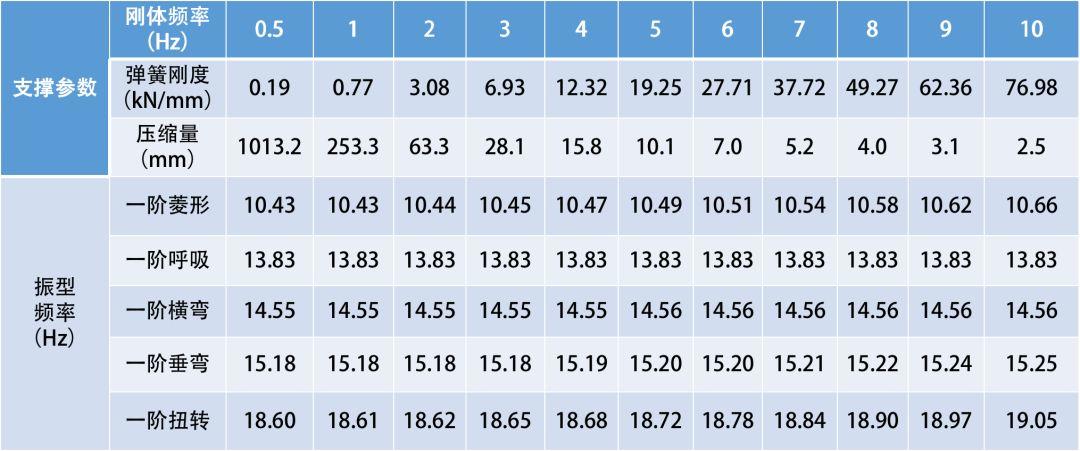
表5 车体弹性支撑作用下的模态频率
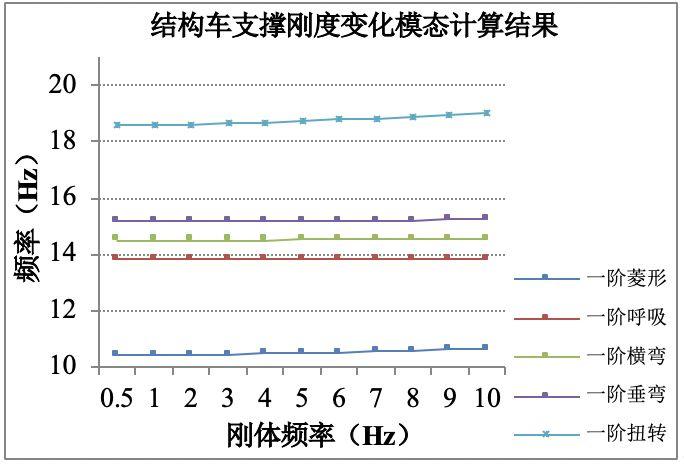
图8 结构车体频率变化趋势线图
结论
结论
通过计算与试验对标以及结构车体支撑刚度的研究,得出以下结论:
1)该研究对象整备状态下一阶垂弯计算和试验频率均大于标准规定的10Hz,能够满足标准规定的相关要求。计算误差基本在5%以内,其计算结果能够满足目前工程应用的仿真精度要求。
2)结构车体在弹性支撑作用下的各阶模态频率略大于自由模态频率且随着支撑刚度的增大各阶模态频率呈增大趋势。
3)在各阶弹性体频率变化量不大于0.1Hz以及考虑结构车体支撑的稳定性情况下,建议今后用于结构车体模态试验弹性支撑的刚体频率在3Hz~5Hz范围内选取,同时建议对于铁道车辆模态仿真计算可直接计算车体的自由模态。
参考文献
[1]郝鲁波. 客车模态计算与试验[D]. 大连理工大学硕士研究生论文,2005,5
[2]TB/T 3115-2005 机车车辆动力学性能台架试验方法[S]. 北京: 中华人民共和国铁道部,2005
[3]王勖成. 有限单元法[M]. 北京: 清华大学出版社,2003
[4]姚亚涛. 不锈钢点焊车体结构仿真关键计算研究[D]. 西南交通大学硕士研究生论文,2016,5
[5]倪振华. 振动力学[M]. 西安: 西安交通大学出版社,1990




