【Radioss 每周干货】时间步长(Time Step)
本文摘要(由AI生成):
本文主要介绍了数值计算中时间步长的选择问题,特别是针对显式积分法。文章指出,时间步长应该小于临界时间步长△t ≤ △tc,临界时间步长与系统的特征频率有关。对于简单的单质点弹簧振子,临界时间步长可以通过其固有频率计算得出。对于一维线弹性的连续介质,临界时间步长与质量、应力波扩散速度等因素有关。在Radioss中,对于不同类型的单元,临界时间步长的计算方法也不同。此外,文章还介绍了调整时间步长的方法,包括使用比例因子和STOP、CST、DEL等选项。
上一期我们在讲显示和隐式积分法时,我们可以看到时间步长△t 在数值计算时比较重要的变量。尤其对于显式积分法,需要时间步长尽量小,这样数值计算的结果就越精确,当然时间步长越小需要的计算时间越长,选择合适的时间步长能让我们能很快的得到符合工程精度需要的模拟结果。
那么对于一个模型什么样的时间步长是合适的呢?我们需要选用的时间步长时必须小于临界时间步长△t ≤ △tc。那这个临界时间步长又是多少呢?本讲就来为你详细讲解一下~

为使数值计算稳定,在显示积分法中比如对于一个不考虑阻尼的系统,这个临界时间步长应该是与系统的特征频率有关:
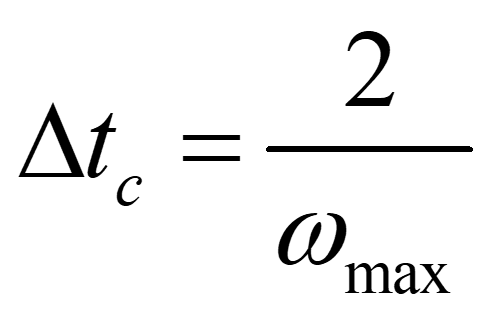
上面这个临界时间步长的公式我们是从系统平衡方程中得来的。
比如在前面的显式积分法中所用的简单的无阻尼的例子来说,我们有
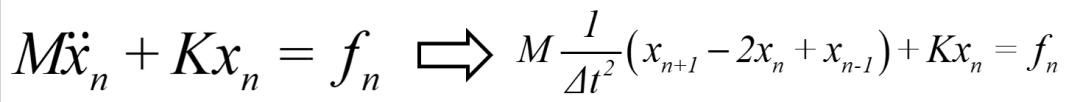
那么上面的公式也换成下面的形式来表达:
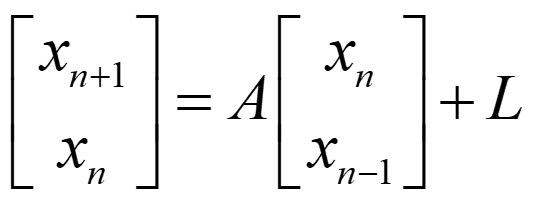
那么这个A矩阵对于这个无阻尼弹簧振子的例子来说就是:

然后计算这个A矩阵的特征值我们得到:
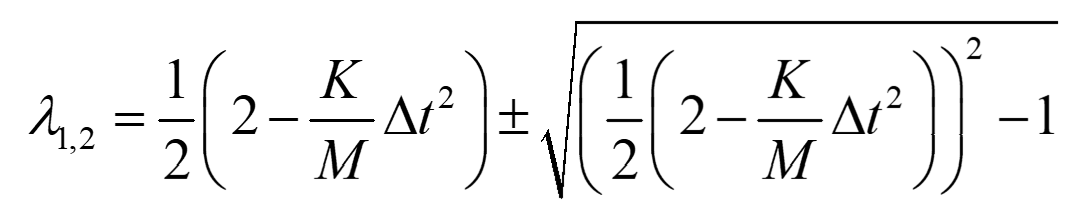
在这个A矩阵的特征值中如果根号里面为负,那么特征值是虚数解。这个将导致了显式积分法计算的不稳定。如果根号里面等于0或大于0时,那么特征值是两个实数解。这时显式积分计算才是稳定的。即根号里面满足 :
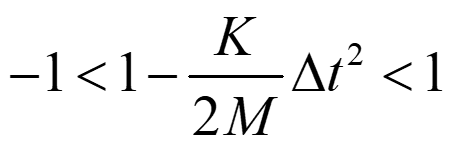
对于简单的单质点弹簧振子我们都知道它的固有频率是:
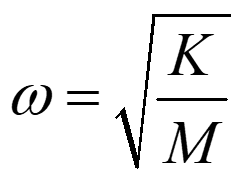
那么用这个代入上面的公式我们就推导出:
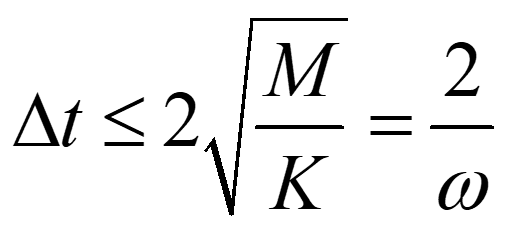
在Radioss中我们对于所有单元采用一个时间步长,所以必须取一个满足所有单元的时间步长,即:
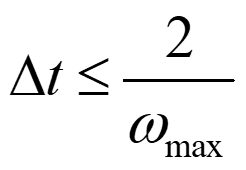
所以我们将

称为系统的临界时间步长△tc。
假使对于一个一维线弹性的连续介质(比如杆单元TRUSS)来说,

那么,


这个质量均分在构成单元的节点上,对于每一个节点上质量为
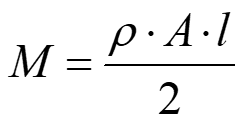
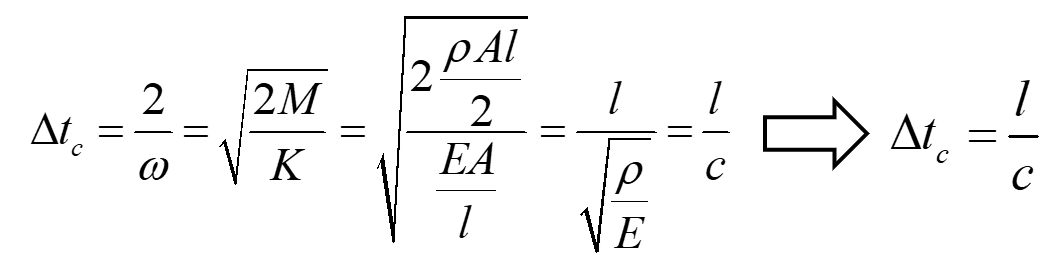
注意在这个例子中系统的固有频率是
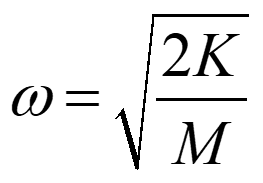
c是应力波扩散的速度,也可称为声音在固体中传播的速度:

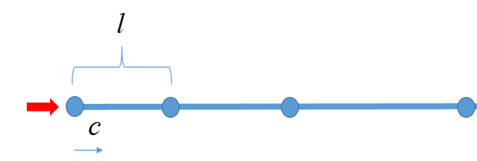
所以在这个例子里临界时间步长:
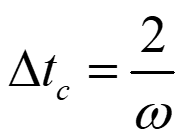
进而也可以说是:
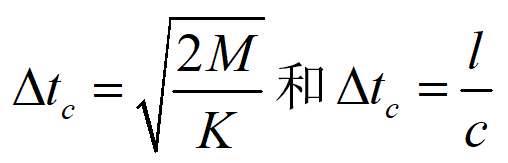
他们的区别就是前面一个是描述离散点的所以用于Radioss中的节点时间步长控制,如/DT/NODA。而后一个是描述连续介质的所以用于Radioss中的单元时间步长控制。如/DT/BRICK, /DT/SHELL, /DT/AIRBAG, /DT/AMS等。
当然还有一些比如 /DT/INTER, /DT/THERM, /DT/GLOB 可以既可以用于节点时间步长又可以用于单元时间步长,具体根据实际情况使用。
那么Radioss对于不同的单元,选取也是不同的。我们将所选用的长度这里称为特征长度。不同单元类型临界时间步长的计算也是不同的。下面我们来大致汇总一下。
杆、弹簧、梁
杆、弹簧、梁
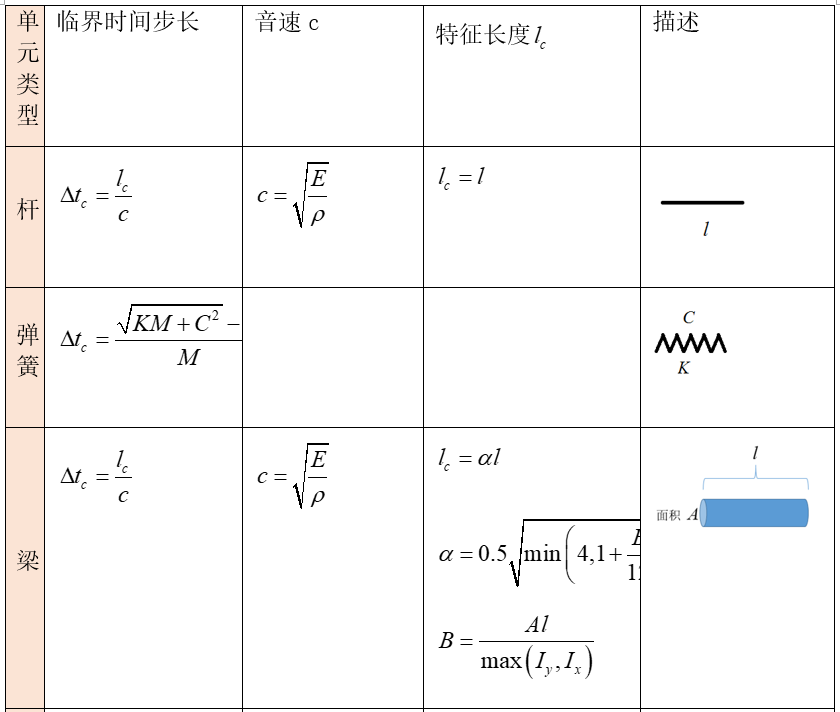
壳单元
壳单元

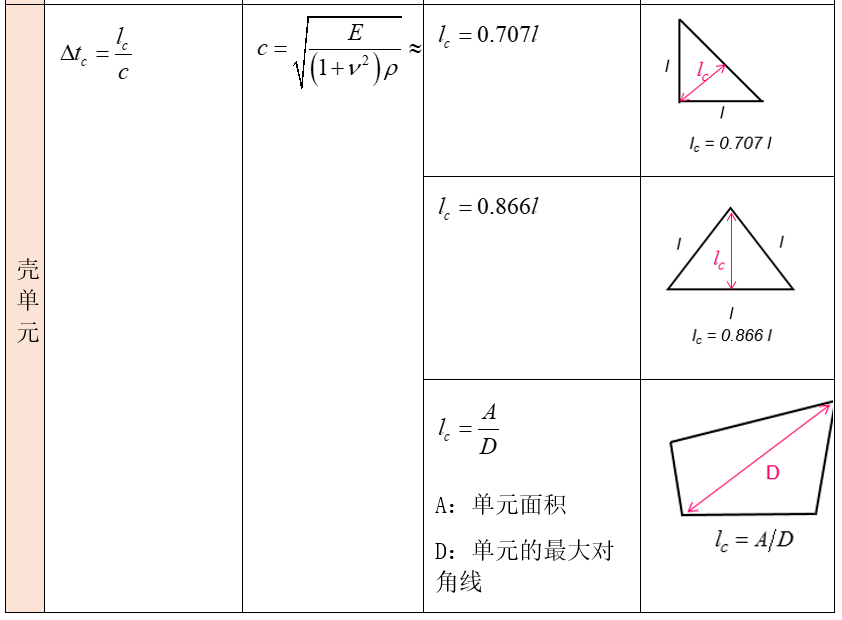
实体单元、接触
实体单元、接触


这里注意在实体单元中由于
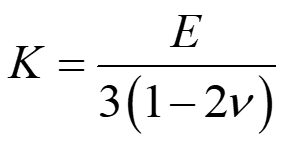
当 v=0.5 时 K 和 c 就无穷大,那么时间步长就会无穷小。所以对于不可压缩材料不要取 v=0.5 而是取 v≤0.4995 就可以。
单元类型选择和单元网格大小从上面的表格中看出对时间步长是有影响的。
Radioss中每一步使用的时间步长是程序内部计算的,那么我们仍然可以通过一些方法来调整时间步长。
调整时间步长
调整时间步长
1
一种方法是用一个取值0到1之间的比例因子△Tsca 乘以临界时间步长来调整。它是用于考虑模型中出现的非线性问题。这个参数在Radioss中默认是0.9。对一些分析中甚至要用户设置更小的值(比如0.66)。比如对于以下情况我们根据临界时间步长应该设置相应的比例因子。

图 I 所示的常见的钢的应力应变图显示,在材料进入塑性阶段后有效E模量是比最初的弹性阶段的有效E模量小的,而且这个有效E模量也是渐渐变小的。所以临界时间步长是变大的,这个时候我们一般不需要用比例因子来将时间步长变小。所以使用默认的0.9就完全可以满足了。而图 II 中显示的有效E模量是渐渐变大,图 III 中显示有效E模量是在某一区域后突然变大的,(比如像泡沫橡胶等材料)这时临界时间步长就会变小。那么这时我们需要通过比例因子来进一步调小Radioss计算时使用的时间步长,以满足数值计算的稳定性。
2
另一种方法是用Radioss中控制时间步长的卡片中用STOP,CST,DEL等选项来控制,即如果当前的时间步长到了用户给定的最小时间步长那么计算就终止(STOP),或就使用用户给定的最小时间步长来继续计算(CST),或将导致时间步长小于用户给定的最小时间步长的单元删除(DEL)。
当我们在节点时间控制(/DT/NODA)时使用了CST选项。那么当模型计算过程中由于非线性原因导致临界时间步长不断变小,而Radioss实际使用的时间步长也跟着变小,当到达用户设定的最小值后由于CST选项,时间步长就不会再变小,但是这样下去会导致整个计算的不稳定,Radioss使用局部增加微小质量的方法, 来将临界时间步长增大,从而维护数值计算的稳定性。

那么这个局部增加的质量可以通过使用/ANIM/MASS在HyperView中看出。但是我们也不能无限制让Radioss的增加质量(通常局部质量增加不要加倍),也就是我们不能在CST中设定太大的最小时间步长。因为我们毕竟要保证在非线性动态数值分析中遵从质量守恒、能量守恒、动量守恒。增加质量这样的数学上的解决方案也要符合实际物理问题(或者至少不能与时间物理情况相差太大)。不能因此增加太多的动能。否则数值计算的结果正确性会受影响。




