【HyperWorks优化实例向导】之高考数学一题九解及梁单元优化
本文摘要(由AI生成):
这篇文章主要介绍了 HyperWorks 优化实例向导中梁单元的优化,包括拓扑优化、形状优化、尺寸优化和换截面等内容。文章还介绍了使用 HyperStudy 进行结构优化的流程,包括定义参数、设置优化目标和约束、选择设计变量、运行优化算法等步骤。此外,文章还介绍了一些其他的优化方法,如尺寸优化、使用 Tpl 的 if 表达式控制 fem 文件中相应单元的有无、使用 Compose 和 Python 进行符号求解和数值求解等。最后,文章公布了一道高考题的不同解法。
HyperWorks优化实例向导第二期来啦!每一篇系列文章都会围绕一个主题,以实例为向导,提供模型和操作视频,以便让有兴趣的读者可以在自己的电脑上重现整个过程。本期我们来说说梁单元~
梁单元虽然看起来简单,却很重要。因为很多大型结构都是由梁单元搭建起来的。鸟巢设计方 ARUP 是Altair的全球大客户,他们用Altair OptiStruct™和Altair HyperStudy™ 优化他们的产品。

梁单元的建模和梁截面的建模已经在《【HyperMesh宝典】之梁单元》等文章中详细介绍过了。
这一期只讲梁单元的优化,包括拓扑优化、形状优化、尺寸优化和换截面等。依照惯例还是主要以举例的方式说明,并一如既往地提供操作视频和模型(下载链接在文末)。
引子
引子
在这沉闷的岁月里,应该有愉快的题目才对,以一道高考题作为引子:
高考题
曾经参加高考的你不妨先自己试试看能不能凭自己的聪明才智解出解析解。
除了高考解析解法,本文还给出了Compose / HyperStudy / HyperMesh / HyperGraph 解法, templex 解法,MotionView / MotionSolve / python numpy / python symbol 九种解法。提供了HyperMesh / MotionView / MotionSolver / HyperStudy 解法视频,在文末可以获取下载链接。
OptiStruct 解法直接在接下来这道题中展示,就不在这个小题上试牛刀了。
形状优化:
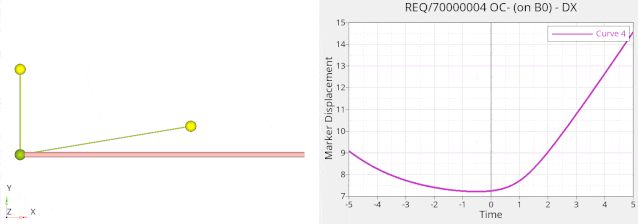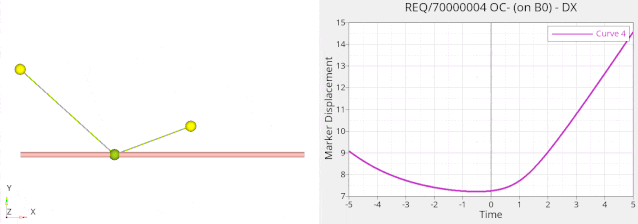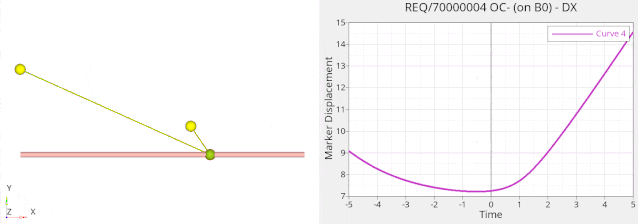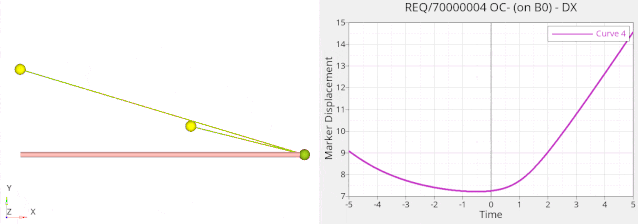
下图是一个管道示意图,1,2,3是三个村庄,水平线是一个管道,现在希望重新设计两个小红点之间的管道以缩短管道总长。因为截面一致,体积最小化就相当于长度最小化,这样可以免去计算距离的麻烦。

优化三要素:
目标:体积最小化
约束:无
设计变量:连接点位置x向和y向两个形状变量
优化结果如下:

总的体积减小了多少呢?请看优化迭代图:

以上纯属娱乐,接下来才是梁单元优化的正经技术。
拓扑优化
拓扑优化
话说拓扑优化是解决结构优化问题的首选,无论 1D - 2D - 3D 基本上都是一样。
假设要在山坡上建造类似过山车轨道的结构,需要在轨道的下方按照一些 z 向的金属支撑柱,由于坡度、轨道方向等变化,不同位置的载荷大小和方向各不相同。

本例是一个简化模型,仅对支撑柱的安装位置进行优化。顶部的轨道部分作为非设计空间保留,整体模型如下图所示:

优化三要素:
优化变量:所有支撑柱单元
设计约束:设计空间的剩余体积 < 50%
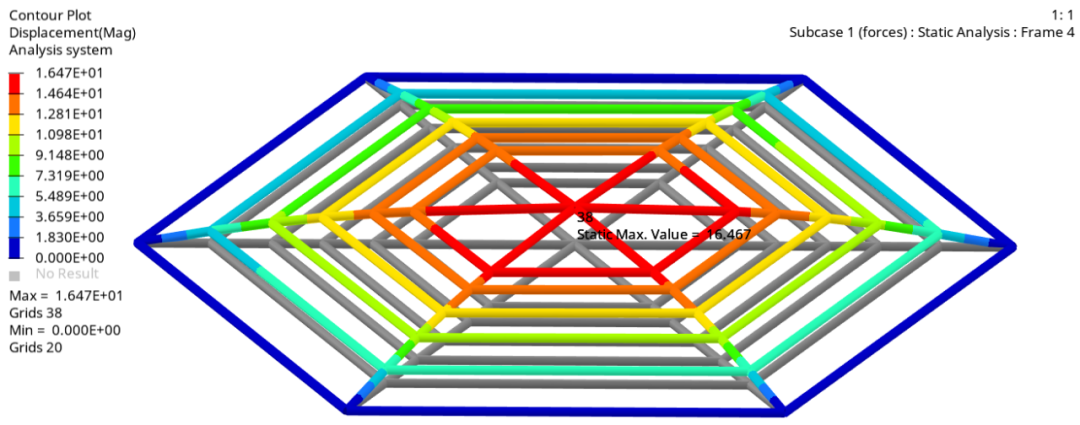
优化目标:最小化轨道的最大位移
优化需要考虑40个工况,每个工况的位移约束都是支撑柱底部的全约束,每个工况载荷的施加位置及大小方向各不相同(载荷和工况的建模比较复杂,二次开发视频教程中有个脚本是针对这个模型的):
优化过程的主要步骤如下:
创建设计变量,props 只选择 support_design

(点击图片可查看高清大图)
创建体积百分比响应,props 只选择 support_design

创建位移响应
nodes选择轨道上的所有节点。

创建位移的目标参考

创建目标为最小化最大位移

提交计算并查看优化结果
为了更好的显示梁单元,在HyperView的Preferences > Options下拉菜单中将所有1D单元显示为圆柱。

优化结果的密度云图显示如下:

利用Iso工具,密度大于0.5的支撑柱如下图所示:

1D 单元的拓扑优化还经常被用于焊点/铆钉/胶等连接件的优化,可以用于找出关键连接位置或者减少焊点。大家可以在历年Altair用户大会文章中找到很多篇客户应用文章。下图是某客户进行焊点位置优化的模型,典型工况是全局刚度和低阶模态。

尺寸优化
尺寸优化
01.梁截面的尺寸优化
以工字梁 PBARL 为例,OptiStruct 帮助中有两种工字梁,I 和 I1,截面尺寸如下:

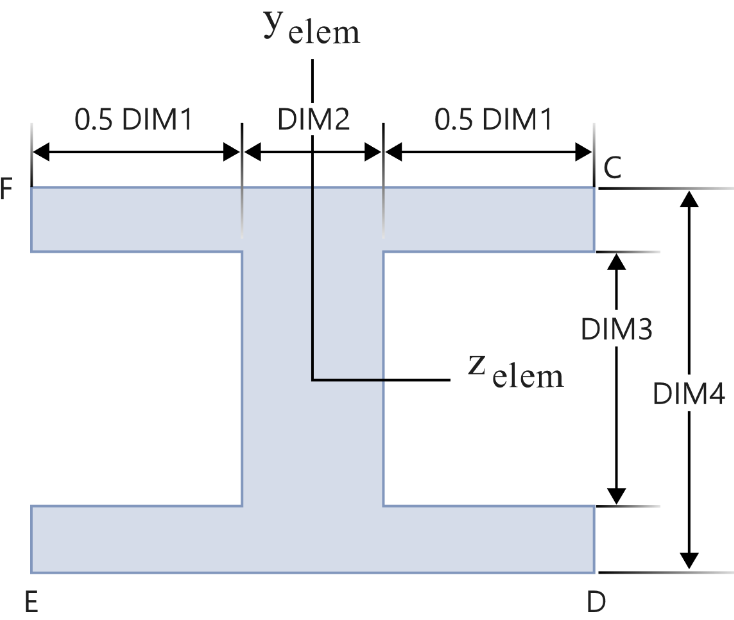
以 I 型截面的DIM1为例:
进入size(parameter面板)创建一个尺寸变量

关联尺寸变量到属性项,prop 选择一个 PBARL 属性,designvars 选择刚刚创建的 dim_1

这样就完成了工字梁的高度尺寸的变量创建。每个工字梁有4个尺寸,如果要创建下图(照片摄于2018年bauma工程机械展)的所有梁的尺寸变量,工作量有点大。

早在《【HyperMesh宝典】之OptiStruct优化变量》一文中已经介绍了梁单元尺寸优化的例子。
梁单元的尺寸优化的困难不仅仅在于大量梁单元设计变量的定义比较麻烦(针对特定问题编写脚本是一个比较快捷的方法)。梁单元类型繁多,HyperMesh并没有给出简单易行的批量创建梁单元截面尺寸变量的方法。
而且梁单元的尺寸通常都不是独立变化的,比如管状截面的外径必须大于内径,工字梁的各个尺寸也有相互约束。OptiStruct可以使用DLINK或者DLINK2定义尺寸约束关系,HyperStudy也支持变量之间施加约束关系,具体用法同样可以参考【HyperMesh宝典】之OptiStruct优化变量。
实际上很多结构都是使用型材连接在一起的,型材的尺寸不能随意定义,只能选用市场上供应的规格。
为了解决这类问题,用下面这个简化的垳架的梁截面类型优化来演示解决方法。

本例的方法可以解决如何选择截面的问题,例如在以下截面中该选择哪种:

或者在下列同类型的截面中选择哪一个:

为了便于加工制造,截面的类型不宜太多,而且同一根梁应该选用同一截面。
考虑可能存在的几何大变形问题,该分析模型采用OptiStruct带大变形的准静态分析。工况设置如下:

为方便后续操作,将模型分成了9个component并分别进行了单元ID号控制,使每个component的单元id都在各自范围内,这样方便文本编辑器选择同一个component的单元。组件情况如下图:


计算位移结果如下图:

接下来需要从 fem 文件生成一个 templex 参数化模型。这是最关键的步骤。生成的部分tpl文件内容如下:
在文件开始创建9个变量
{parameter (tube1, "tube1",10, 10, 40)}
{parameter (tube2, "tube2",20, 10, 40)}
{parameter (tube3, "tube3",20, 10, 40)}
{parameter (tube4, "tube4",30, 10, 40)}
{parameter (tube5, "tube5",30, 10, 40)}
{parameter (tube6, "tube6",30, 10, 40)}
{parameter (isec1, "isec1",2, 1, 3)}
{parameter (isec2, "isec2",2, 1, 3)}
{parameter (isec3, "isec3",2, 1, 3)}
在相应部分引用这些变量

以上工作都在文本编辑器里面完成,具体可以看课件压缩包内的操作视频。
这些 templex 的编程语法可能让你困惑,好在我们已经准备了成套的templex视频教程。下载方法见本文结尾。
打开HyperStudy进行模型设置

优化响应为体积和加载端的位移。
用 DOE 可以找出各因子的影响大小,这里采用默认的 Mels DOE 算法生成61次试验。根据2-8定律:80%的成果是由20%的投入产生的。下图可以看到体积主要由前三个变量决定,变形主要由前五个变量决定。

通过全局响应面法或遗传算法得到最佳设计
优化三要素如下:
优化目标:最小化体积
设计约束:节点223的位移<=40mm
设计变量:梁截面的类型
从优化结果可以看到最大位移和体积的散点图如下,右边的点体积大,泡泡大小代表最大位移的大小。可以看到总的来说体积大的变形小(符合常理),但是如果设计不好也可能出现体积位移都很大的情况(例如最上面的那个泡泡)。

最大位移和体积的散点图
蛇形图直观地看到所有优化设计方案(从左到右的每一条线代表一次试验):
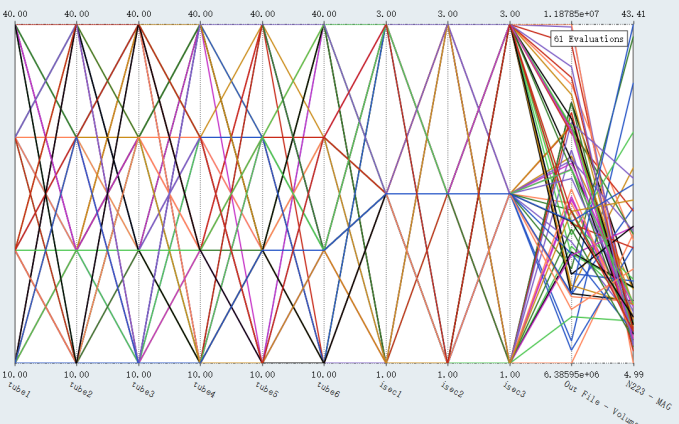
蛇形图
当然,最最重要的是优化得到的结果到底有多优秀,体积降了多少,请看下图的迭代历史曲线,左图的体积下降简直是飞流直下三千尺。

Q
除了换个截面形状,能不能优化梁的有无呢?
A:当然是可以的,有很多种方法。
前面拓扑优化的例子已经大概实现了这个功能,但是问题在于优化结果会有很多中间密度单元,如果结果只要0和1就好了。
最简单的方法是直接进行尺寸优化,比如把尺寸设置为离散值,一个取值是接近0的值(不能真的是0,否则求解器会报错),另一个是当前设计值。
或者为梁赋不同的材料,把弹性模量E作为变量。
这些方法都太传统了,我们要介绍的是另外一种:直接通过tpl的if表达式控制fem文件中相应单元的有无。
为了方便起见,我们将使用 include 文件。可以在 HyperMesh 界面右击创建 include 文件,然后把相应的 component 鼠标左键拖拽到对应的 include 文件即可。

注意到 node 信息需要保留在 master 文件里,否则一旦这个子 include 文件不在了,整个模型都无法求解了,所以拖拽过程弹出的下图对话框需要设置如下:

然后在文本编辑器里面建立设计变量和if表达式如下(为了方便记忆把变量范围取为了3,4,5,6,和include文件的名称一致):
{parameter(var1,"var1",3,3,6)}
$$ optistruct
SUBCASE 1
LABEL NONLINEAR
ANALYSIS NLSTAT
SPC = 1
LOAD = 2
NLPARM = 3
NLADAPT = 5
NLOUT = 4
BEGIN BULK
{if (var1 == 3)}
INCLUDE 'c3'
{elseif (var1 == 4)}
INCLUDE 'c4'
{elseif (var1 == 5)}
INCLUDE 'c5'
{else}
INCLUDE 'c6'
{endif}
这段tpl文件实现了下图左侧4个结构的四选一功能。
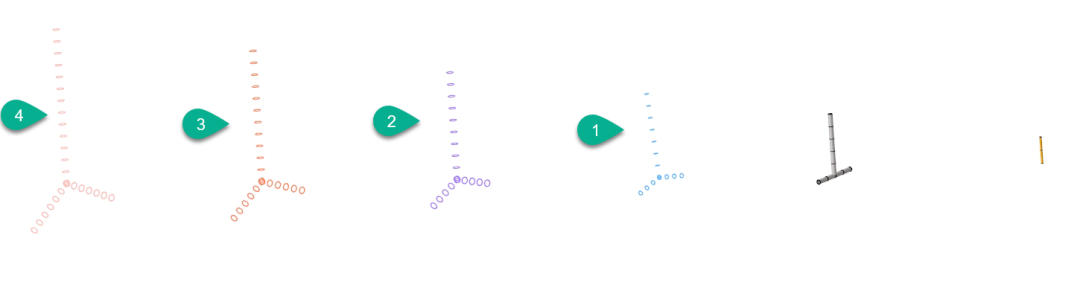
也可以实现独立决定每一个结构的有无,只需要把取值范围变为0或1即可。

{parameter(var3,"var3",1,0,1)}
{parameter(var4,"var4",1,0,1)}
{parameter(var5,"var5",1,0,1)}
{parameter(var6,"var6",1,0,1)}
$$ optistruct
SUBCASE 1
LABEL NONLINEAR
ANALYSIS NLSTAT
SPC = 1
LOAD = 2
NLPARM = 3
NLADAPT = 5
NLOUT = 4
BEGIN BULK
{if (var3 == 1)}
INCLUDE 'c3'
{endif}
{if (var4 == 1)}
INCLUDE 'c4'
{endif}
{if (var5 == 1)}
INCLUDE 'c5'
{endif}
{if (var6 == 1)}
INCLUDE 'c6'
{endif}
建议大家自己动手试一下,亲手成功一次自然就明白了。我提供了操作视频。下图是其中一个DOE模型:

虽然这里讲的模型都是梁单元,但是如果include文件里面的内容是2D/3D单元也是一样可以的哦。不信的话可以自己尝试一下~
此外,下载链接里面还提供了一个Radioss冲击工况的HyperStudy形状优化模型和视频(简单的形状变量)。
高考题答案公布
高考题答案公布
接下来该公布高考题的答案了。
作为一名工程师,我的习惯是先用 Compose 画个图偷看一下答案😄,最小值在7.2左右,对应的x在-0.5左右。Compose 算法中的一部分是和 HyperStudy 类似的,比如遗传算法、序列二次规划法等等。注意右下角有一堆求解优化函数可以帮忙找出最优解。

解析解法
先把y写成如下形式:
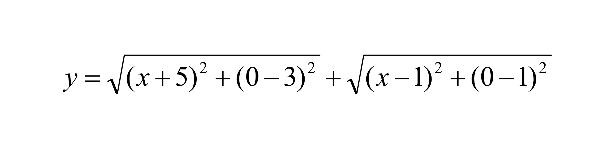
因为两点距离公式就是这么写的,y就是(x, 0)点到(-5, 3)和(1, 1)两个点的距离之和。
根据几何意义画图:
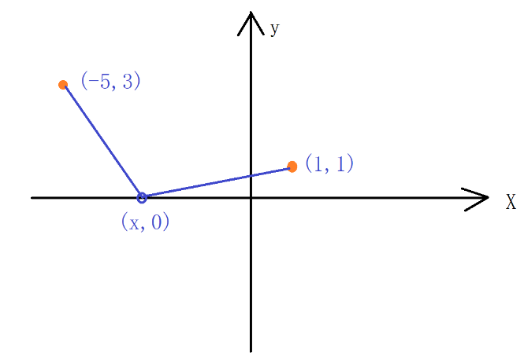
根据对称性,(x, 0)到(1, 1)和(x, 0)到(1, -1)距离相等,所以可以将(1, 1)关于x轴镜像后再连接(-5, 3)。很显然最短距离在三点共线时达到。
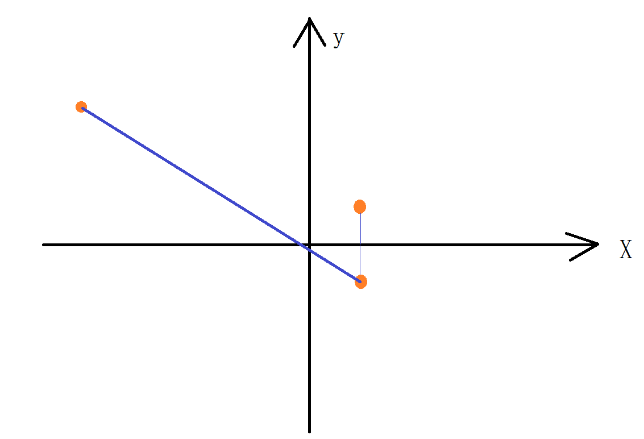
最后利用直角三角形斜边计算公式即可得到答案(无理数):

符号求解工具
也可以通过一些符号求解工具直接得到符号形式的解析解。
例如可以访问如下网址直接输入表达式得到解析解:

也可以使用一些商用符号计算软件,但不在本文讨论之列。
Compose / python
Compose 带了大量的python的科学计算工具库,例如 numpy、sympy 和 matplotlib 等。这里先用符号运算工具包 sympy 求解一下。

也可以在 numpy 中进行数值求解,并用 matplotlib 绘图:

python代码很容易懂,就不多解释啦。
Compose优化解法如下,直接贴个图就够了。
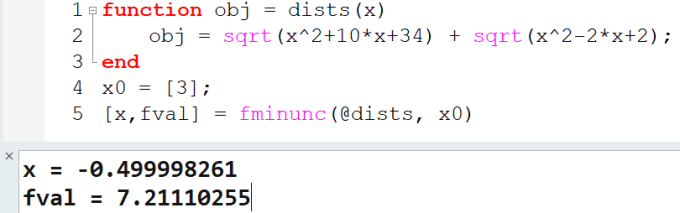
HyperGraph / templex
HyperGraph 和 TextView 解法如下图所示,看不懂右边代码的请参考templex教程。

得到曲线和标签如下图:
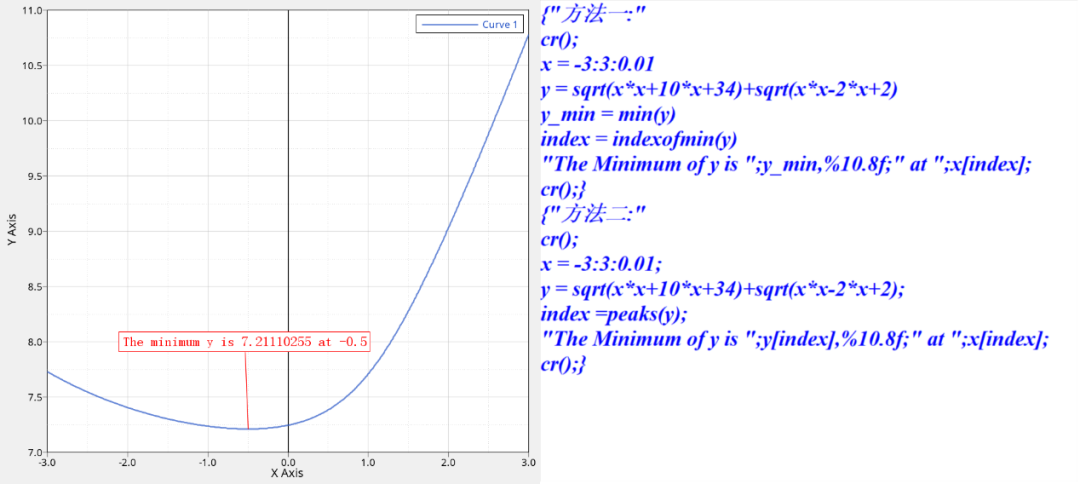
运行 templex 后结果如下:
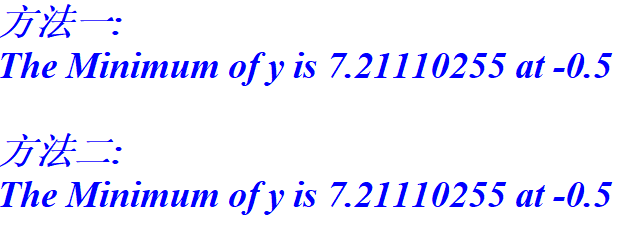
MotionView/MotionSolve
MotionView/MotionSolve的结果如下: