【Flux技术专题】工程电磁场数值仿真与应用 - 理论入门
本文摘要(由AI生成):
本文首先介绍了电磁场数值计算的理论基础,包括电磁场理论基础、电磁学问题分类、电磁场数值计算方法的分类、电磁场的边值问题、电磁场问题边界条件以及电磁场数值分析对电磁问题的描述。接着,文章介绍了数值计算中单元离散的重要性,以及工程电磁场数值计算的有限元方法。有限元方法应用广泛,因为它具有灵活性、易于处理边界条件、简化矩阵方程组求解等优点。文章还详细介绍了电磁场有限元仿真的步骤,并提供了磁场数值仿真示例 Demo。
全新技术专题《Altair Flux™工程电磁场数值仿真与应用》系列上线啦!
后续我们会定期更新一些技术短视频,主要针对具体应用,方便大家在碎片时间快速学习,本期我们从理论入门开始讲起~
不论采用哪种电磁场计算工具,其都得满足遵循电磁场的基本规律,学习理解电磁场的基础理论对掌握数值仿真方法、正确评价仿真结果以及深入理解软件操作都是有益的。
Altair Flux是专业的低频电磁场仿真工具,其所有分析应用都满足电磁场基本原理:Maxwell方程组。
1
电磁场理论基础
1
电磁场理论基础
Maxwell 方程组

所有的宏观电磁问题都满足Maxwell方程组
四个Maxwell方程组的物理学意义解释如下:
全电流定律(安培环路定律)
产生磁场的旋度源是电流(传导电流密度+位移电流密度)
变化的电场也产生磁场(传导电流+变化的电场)
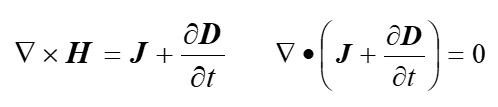
磁通连续性原理(磁通高斯定律)
磁场是无源场(磁力线总是闭合曲线)

流进一个闭合面的磁通量等于流出的磁通量
法拉第电磁感应定律
变化的磁场也会产生电场 (电荷+变化的磁场)

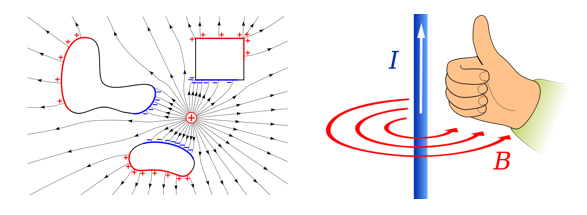
高斯定律
表明电场是有源场,电场的源是电荷
电荷以发散的方式产生电场

穿过某闭合面的总电通量等于该面所包围的总电荷量

Maxwell方程组加上洛伦兹力的计算公式,合起来构成了静止及运动媒质中电动力学的基础,概括了发电机、电动机和其他电磁装置的工作原理,也概括了电磁波的发射、传播和接收的原理,正确反映了电磁场中各物理量之间的相互关系。
电磁学问题分类
低频(准静态场,忽略波动效应)
高频(电磁波的传播)
电磁场的类型
稳恒场
静电场
恒定电流场
恒定磁场
时变场
瞬态电场
瞬态磁场

2
电磁场数值计算
理论基础
2
电磁场数值计算
理论基础
什么是计算电磁学?
以电磁场理论为基础,以高性能计算技术为手段,运用计算数学提供的各种方法,解决复杂的工程问题。
电磁场数值计算的理论和方法是计算电磁学的重要组成部分,其任务是在已知设计方案的条件下通过数值分析的手段对方案进行评价,属于电磁场正问题。即:
已知给定区域的几何结构、物理参数
求解一个电磁场的定解问题(获得电场、磁场分布及各特性参数)
电磁场数值计算的关键要素
电磁问题数学模型的控制方程
场域的离散化
电磁场数值计算方法的分类
从数学模型中控制方程的形式上分:微分方法和积分方法
从场域离散化方式上分:场域元法、边界元法、和等效源法

电磁场的边值问题
求解某一确定区域内满足定解条件的电磁场方程的问题
定解条件:区域边界条件、时变场初始条件
矢量场唯一性定理
一个矢量场被它的散度、旋度和边界条件(矢量的方向或切向分量)唯一地确定。
为了便于求解矢量方程,可通过位函数将电磁场方程进行改写,构成电磁场的位方程。
电磁场控制方程的位函数变换

对电磁位(磁矢位、电标位)施加一定的约束条件,即假设电磁位满足某种规范条件,则可进一步简化电磁位波动方程,电磁位的规范变换满足规范不变性。
电磁位的波动方程与规范
a) 洛伦兹规范(求解域内不存在导电媒质,且电流密度J 已知)
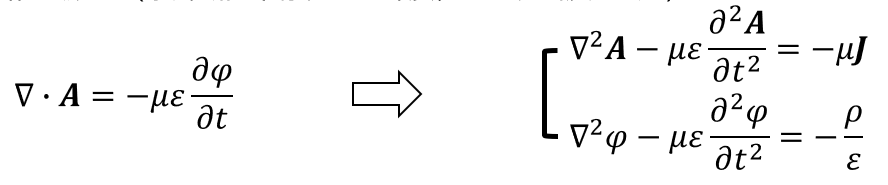
b)电导率规范(时变磁场中,求解域内存在导电媒质,其中产生感应涡流,忽略位移电流密度)
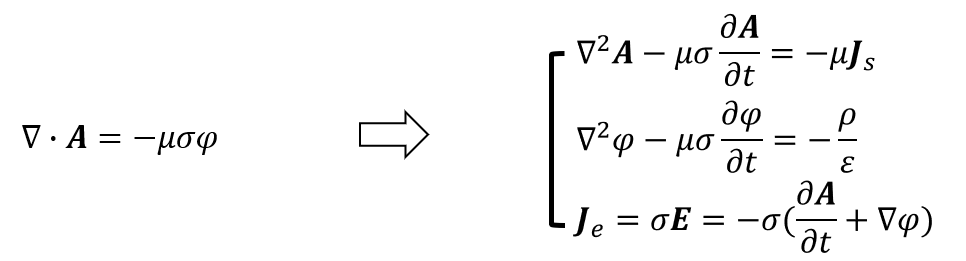
c)库仑规范(静态场,场量不随时间变化)
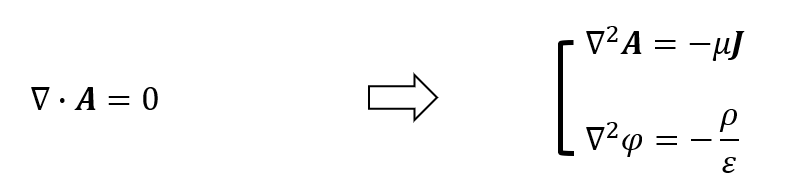
通过对电磁位方程应用适当的规范变换,实现了A和φ的解耦,电磁场计算成为求解A和φ单独满足的微分方程。
工程电磁场问题中,求解区域内包含不同性质的媒质,为了减小计算规模,往往将求解区域分成不同性质的子区域,在其中采用不同的位函数作为未知函数建立微分方程。
由于两种媒质的交界面上电磁特性发生突变,微分方程在交界面上不成立,在分区列出电磁位方程基础上,同时需要列出交界面条件,从而将不同区域的微分方程关联起来,联立求解。
工程电磁场(低频)
针对工程电磁场即低频电磁场,认为其电磁场随时间变化相对缓慢,当电磁场随时间缓慢变化时,方程中的

约等于0,此时称为准静态电磁场,具有静态场的一些性质。

低频电磁场中电场与磁场是解耦的
电准静态场方程


电准静态场中只计算电场物理量,不计算磁场物理量。
磁准静态场方程


产生磁场的源是电流密度。
变化的磁场产生感应电场,
导体中形成感应电流 (J=σE)
时变磁场可按磁准静态场处理的条件:
导电介质:ωε≪σ
理想介质:R≪λ
对于纯金属(良导体)而言,σ≈10^7S/m,ε≈ε_0,则 ω≪10^17 1/s,即在导体中一直到紫外波长都可以忽略位移电流。
电磁场问题边界条件
当求解区域中包含多种媒质时,实际上场的控制方程时对应于每种媒质分区列写的。
不同媒质的分界面条件

位函数在不同媒质分界面条件


电磁场能量并非局限于有限区域,实际为开域问题,数值计算中存在场求解域边界。
场域边界条件:
1. 无穷远截断边界条件(第一类齐次边界条件)

2. 垂直边界条件(第二类齐次边界条件)

3. 对开域问题、对称问题的处理

电磁场数值分析对电磁问题的描述

场域边界条件、时间初始条件

单元离散
数值计算需要将连续的求解区域离散成为许多单元,用这些单元的集 合来表示整个区域,把寻找具有无限多自由度(未知量)的解析解任务降低为寻找有限个单元节点上的自由度的数值解。

单元离散的过程称为“网格剖分”,离散后的模型称为网格模型,连续域的电磁场方程变成离散的矩阵方程。

工程电磁场数值计算的有限元方法

工程电磁场数值计算中,以有限元方法应用最广泛:
有限元网格具有很大的灵活性,支持不同类型的单元形状,能适应复杂的几何形状
基于有限元法的离散化方程的系数矩阵具有稀疏对称特点,大大简化矩阵方程组的求解
边界条件的处理容易并入有限元数学模型,易于编程
有限元方法对整个场域空间进行网格离散,网格生成任务繁重,单元/节点数量大


电磁场有限元仿真步骤

电磁场问题仿真示例

磁场数值仿真示例Demo





