【HyperWorks优化实例向导】优化起点
HyperWorks优化实例向导第五期来啦!上一讲我们讲解了喷灌系统的水量均匀性分析和优化,本讲目的只是让大家了解优化起点对结果的影响,大部分情况下你并不需要去调整这些参数。
本文摘要(由AI生成):
这篇文章主要讲解了在 HyperWorks 中进行优化时,优化起点对结果的影响。除非遍历设计空间的所有可能,否则得到的设计是否为最优解永远是个谜。作者通过一个喷灌系统的水量均匀性分析和优化的实例,说明了大部分情况下并不需要调整优化起点的参数。接下来,作者通过使用 Compose 和 HyperStudy 进行函数可视化,展示了不同起点对优化结果的影响。同时,作者指出绕过局部最优解最理想的办法是从优化算法入手,并介绍了不同优化算法的比较。在 OptiStruct 的优化中,作者也提到了类似的问题,并提供了一些提示和建议。最后,作者总结了全文,强调了选择合适的优化算法和调整优化起点的重要性。
引言
引言
除非把设计空间所有的可能都尝试一遍,否则你得到的设计是否是最优解永远是个谜。
全局最优只是一个理想
优化就像爬山坡,所有人都希望到达最高点,下面这个图大家应该都比较熟悉,如果起点是A,最终可能只能到达3号峰,如果起点是B那么可能可以到达1号峰或2号峰。

由于只有两个自变量,可以在Compose中进行函数的可视化。Compose代码及图片如下:

HyperStudy优化的相关操作已经在前面的文章中反复介绍,这里不再截图赘述了。使用HyperStudy设置不同起点进行优化的过程请看以下操作视频⬇:
视频中的求解器改成了internal math,也就是templex,实际上也可以直接调用Compose作为求解器,只需要把程序简化为输入一个(x, y)点后得到一个z点即可。
这方面的问题放在后续专门介绍求解器的文章中进行介绍。优化结果如下:
优化起点 | 最优解 |
[0, 2] | 8.10 |
[-3, -3] | 3.77 |
[2, 0] | 3.59 |
绕过局部最优解最理想的办法是从优化算法入手,以下例子对不同的优化算法进行了比较,同时也全面讲解了HyperStudy关于这个例子的完整应用,是HyperStudy不错的入门例子。具体可以参考如下视频⬇:
HyperStudy调用不同优化算法的结果对比如下表所示:
优化算法 | 最优解 |
SQP | 3.77 |
ARSM | 3.77 |
GA | 8.10 |
GRSM | 8.10 |
结论
结论
如果你不知道该选择哪种优化算法就选GRSM。遗传算法(GA)效果也很好,可惜计算量实在是吃不消(起步价差不多是单次分析的一万倍),所以通常只在计算量很小的情况或者在响应面上使用。

OptiStruct的优化也有类似的问题。
使用前面文章中用过的一个简单的形状+尺寸优化模型做一个试验,工况是静力分析。模型如下图:
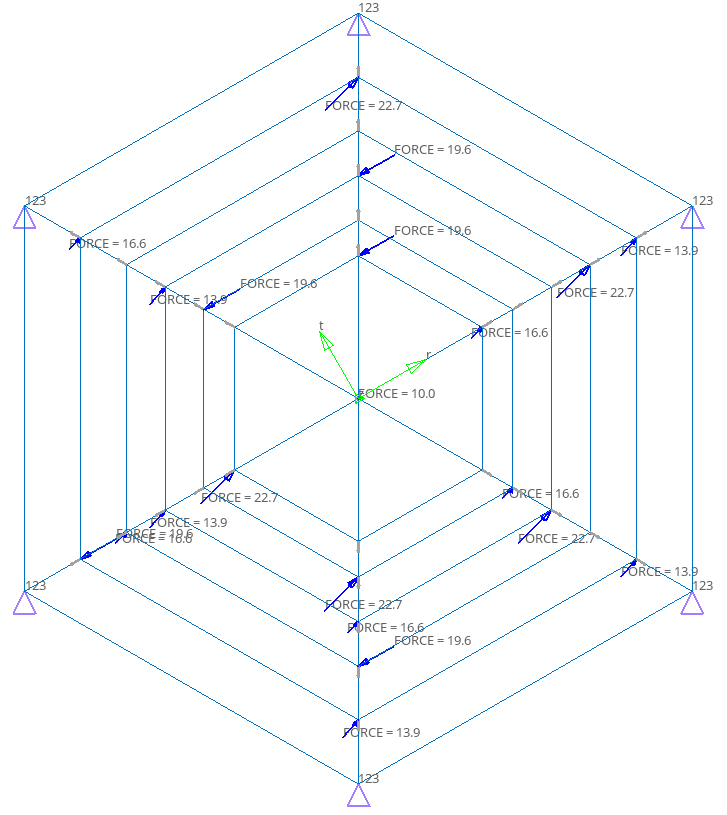
优化三要素如下表:
优化三要素 | 描述 |
形状变量 | 各个环的半径 |
尺寸变量 | 每根梁的半径 |
设计约束 | 中心点位移 |
目标 | 体积最小化 |
不使用DGLOBAL参数的常规优化结果为:850
创建DGLOBAL参数只需要新界面下按CTRL-f,然后输入DGLOBAL后回车,参数一般使用默认值即可(优化20次),如下图所示。
如果你有一颗好奇(或贪婪)的心,可修改如下参数(修改起点的个数):
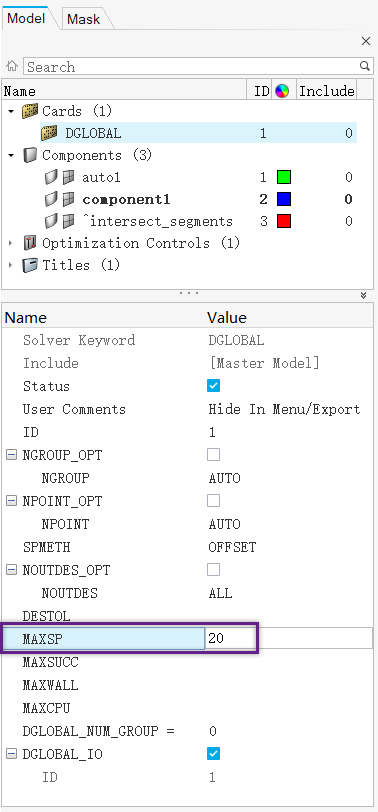
使用默认的DGLOBAL参数优化的结果如下表第二列所示:

画个图直观感受一下差距:

可以看到不同优化起点得到的最终结果也不同,目前的情况是获得11%的提升。万一你的起点不幸是下图中的第二个点,那么付出的代价将获得近50%的超额回报,帮助中有个改进效果很好的例子:OS-T: 5080 Global Search Optimization,大家可以在帮助文档中查看。
提示
提示
选择DGLOBAL进行优化相当于你进行了几十次独立的优化,只是优化设计变量的初始值不同。在写本文的时候作者找了很多线性分析的模型进行优化比较验证,绝大部分模型优化结果只提高了1%~3%。
所以,OptiStruct默认是关闭该选项的。但是你也可能获得很大的提高,特别是优化结果对设计变量比较敏感或者设计变量变化范围很大或者非线性程度比较高的模型。但是对于优化结果的提升幅度我是无法提供任何保证的。
DGLOBAL只支持形状和尺寸优化。如果这类优化问题变量数较少(比如只有几十个变量)也可以使用HyperStudy的GRSM进行优化,一般会有更好的效果。
形状优化或者形状+尺寸联合优化

如果发现OptiSruct优化结果中的形状变量几乎都没有变化,可以将优化的SHAPEOPT项调整为2来强制要求OptiStruct在优化过程调整形状变量的值。设置如下图所示。

拓扑优化

此时无法使用DGLOBAL进行多起点优化。一种变通的方法是手工修改优化的初始密度。具体设置方法是在面板区Analysis > optimization > opti control中勾选这一项并输入初始密度值:

也可以把优化过程当成一次普通的求解,然后使用HyperStudy进行DOE求解,但是拓扑优化往往有数十万个变量,上一种方法已经是够昂贵的了,这种方法计算代价还要高很多倍,不推荐,这里就不演示了。
下图是使用不同的优化初始密度得到的两个优化结果的比较。具体的影响程度取决于具体模型,要不要尝试取决于你有多少计算资源。
当你对优化结果不满意的时候可以尝试改一下初始密度,当然还有控制参数可以影响优化结果,比如离散参数、制造约束等,不要在这一棵树上吊死。





