CFD专栏丨寻找最优解:CFD参数优化案例分享(一)
数值仿真的参数优化
优化,就是寻找最优解。如何定义最优解?
通过数学的方式来定义,比如最小化/最大化某个目标函数。优化是数学和物理相结合的一门学科:数学是优化的工具,物理是优化的实质。
CFD参数优化指的是,以流体相关的变量(如流阻、效率、换热系数等)为优化目标的,基于自由形状、尺寸参数、物性参数、边界条件等参数的优化。
按照优化目标的数量可分为:单目标或多目标优化(MOO-Multi Objective Optimization)。按照学科的数量可分为单学科或多学科优化(MDO-Multidisciplinary Design Optimization )
HyperStudy 参数驱动优化
多学科优化工具 HyperStudy 有两种途径驱动CFD模型:一种是内置的前处理接口SimLab,自动获取变量和提取响应。另外一种是Parameterized File模式,用户手动从求解器文件中提取变量和响应。后者是一种通用方法,也适用于非 HyperWorks 平台的求解器。
支持DOE,响应面拟合,降阶模型、随机分析、多学科、多目标优化。
SimLab支持Inspire/Catia/NX/Creo双向CAD参数传递,HyperWorks CFD支持HyperMorph网格变形参数。
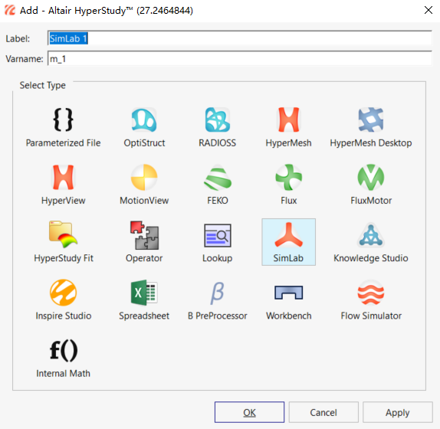
HyperStudy 集成的求解器接口
HyperMorph 基于网格变形,创建Shapes自由形状变量,通常用于管路阻力或气动外形的优化。
HyperMorph定义Shapes
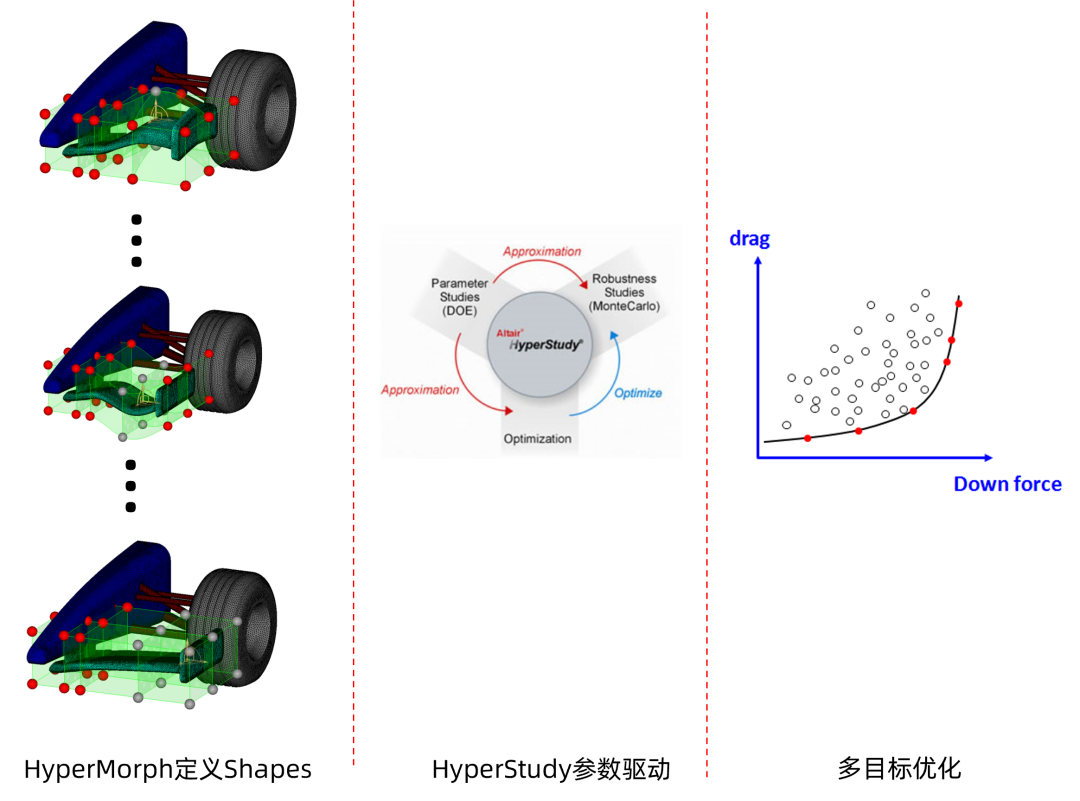
案例:机翼多学科优化
Winglet 用于减少翼尖的诱导阻力,从而提高飞行器的续航能量。但是在翼尖增加的额外重量会导致颤振变大。多学科分析采用PFSI流固耦合模型,气动力的计算结果来自AcuSolve外流场模型,而结构的模态分析结果来自OptiStruct。
优化的目标:减少翼尖Y方向最大变形量,2个约束条件:机翼的升阻比L/D和机翼重量Mass。

机翼Winglet示意图

多学科优化的目标和约束
优化变量,6个几何参数:垂直面倾斜角Cant Angle,小翼长度Length,翼型厚度Thickness,翼尖流向长度Tip length,机翼扭转角Twist angle,翼尖在流向的偏移量x-axis displacement。

Winglet的6个设计参数
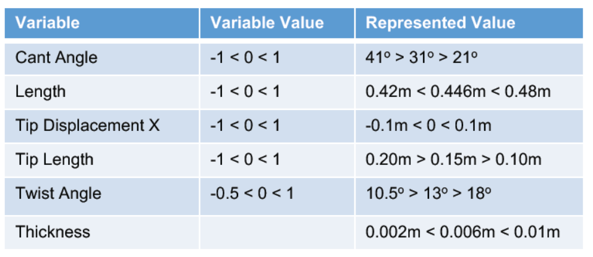
Winglet的6个设计参数的变动范围
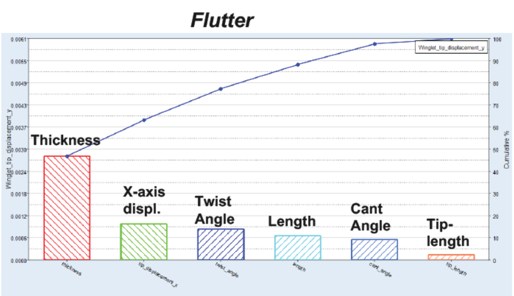
首先采用MELS(修正的可扩展格栅序列法) DOE生成设计空间。Pareto Charts显示Cant Angle和Twist Angle对机翼的升阻比影响最大。
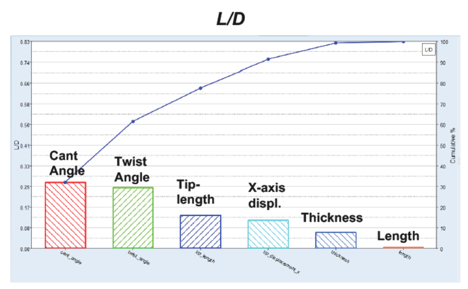
Pareto Charts显示Thickness对机翼的重量影响最大。

Pareto Charts显示Thickness对翼尖变形影响最大。

Winglet外形比较:原始模型(红色),优化后(绿色)
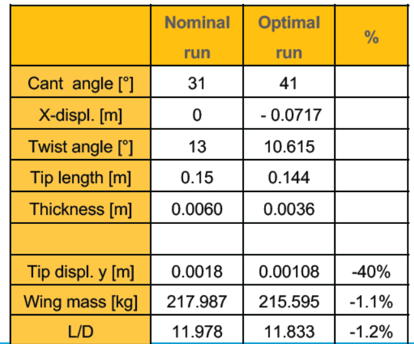
Winglet参数比较:原始模型(Nominal),优化后(Optimal)
采用GRSM全局响应面法迭代57次。优化结果:翼尖Y方向最大变形量减小40%,Winglet重量减少2公斤,气动性能满足约束要求。
案例:拟合试验曲线
某航空电子设备,包含了芯片、PCB板、散热片、冷却通道、和壳体。设备的初始环境温度为0℃,设备经历了升温和冷却的过程,时间历程1000秒。在实验中记录了热源位置的表面温度时间历程。已知冷却边界条件,材料的热物性参数,通过HyperStudy的Area Tool工具可拟合出热源的功率曲线。
观察试验曲线(蓝色exp),发现0~150秒温度迅速上升,150~450秒温度缓慢上升,450~900秒温度缓慢下降,900~1000秒温度迅速下降。因此确定输入参数:5个时间点的热功率,优化目标:预测热功率曲线,使得仿真的温度和试验一致。
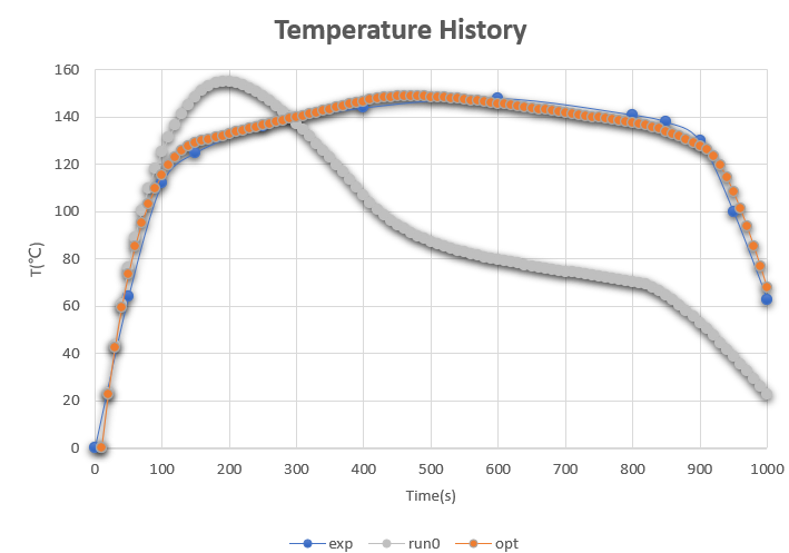
蓝色曲线exp:试验温度
灰色曲线run0:初始参数模拟温度
橙色曲线opt:优化参数模拟温度
优化流程:
SimLab中创建CFD模型,定义初始热功率时间历程曲线
HyperStudy采用参数化文件模式定义优化变量(5个时间点的功率),提取响应 (监测点温度)
导入试验曲线,Area Tool比较两条曲线,将曲线的面积差作为优化目标
ARSM自适应响应面优化算法最小化面积差,26轮迭代后获得最优解
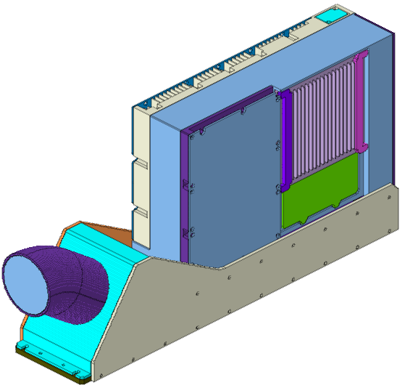

航空电子设备
AcuSolve仿真结果

定义响应曲线
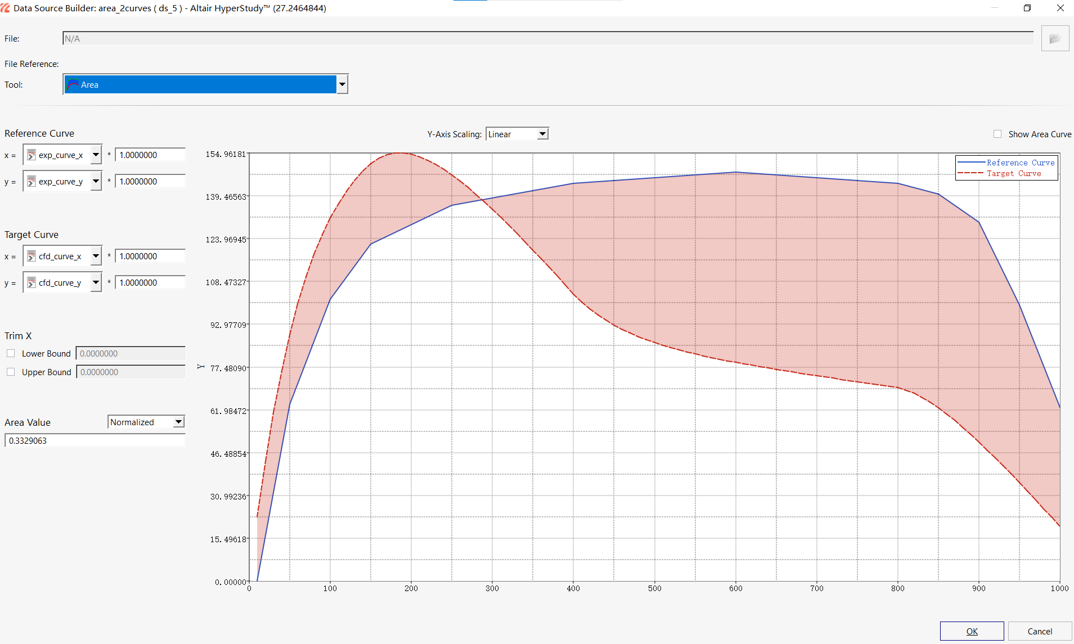
初始参数模拟温度和试验温度的曲线的对比(红色是面积差)
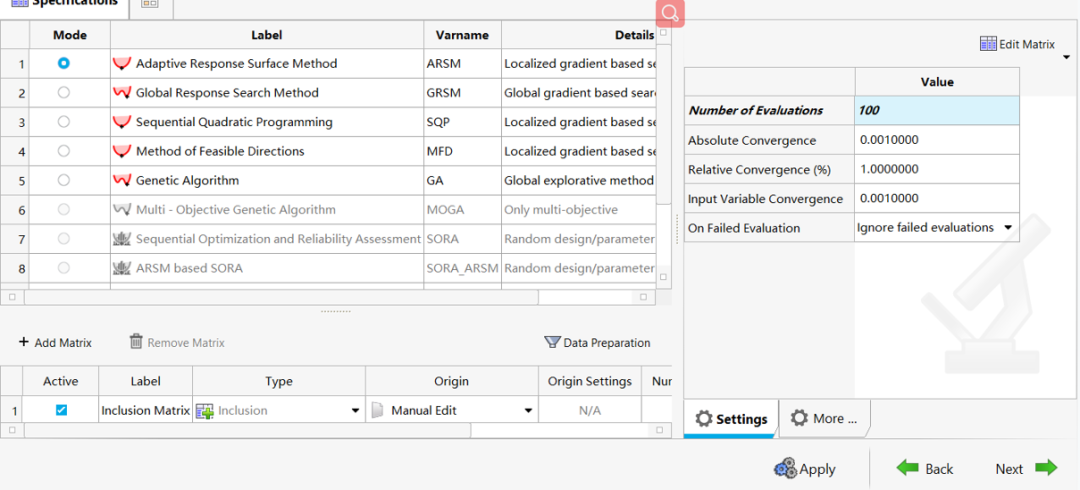
选择优化算法
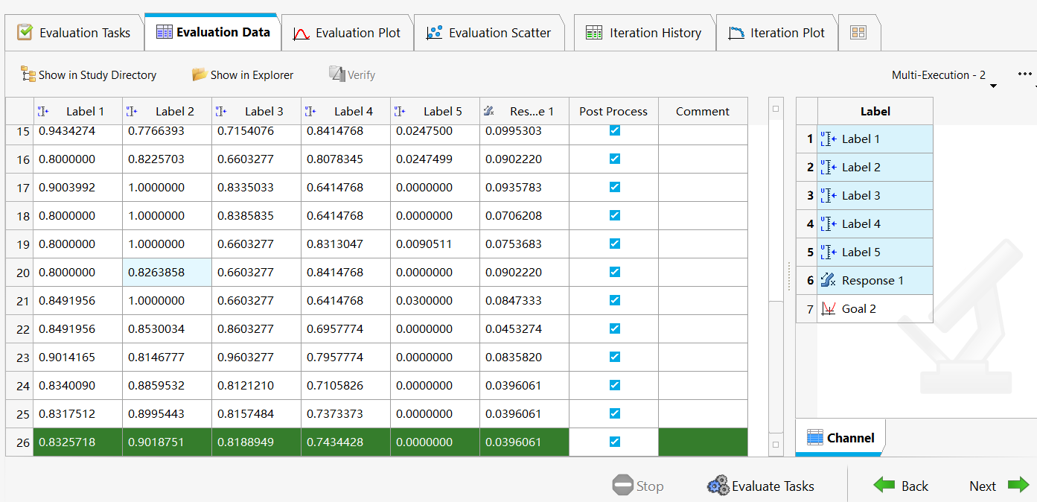
优化过程(绿色是最优解)
案例:一维CFD模型参数的DOE和回归分析
在一维流体模块 Flow Simulator 中搭建涡轮冷却模型,研究轮盘冷却孔的面积和角度这两个形状参数对下游气流旋涡数( Swirl Number )的影响,最终计算出回归方程式。
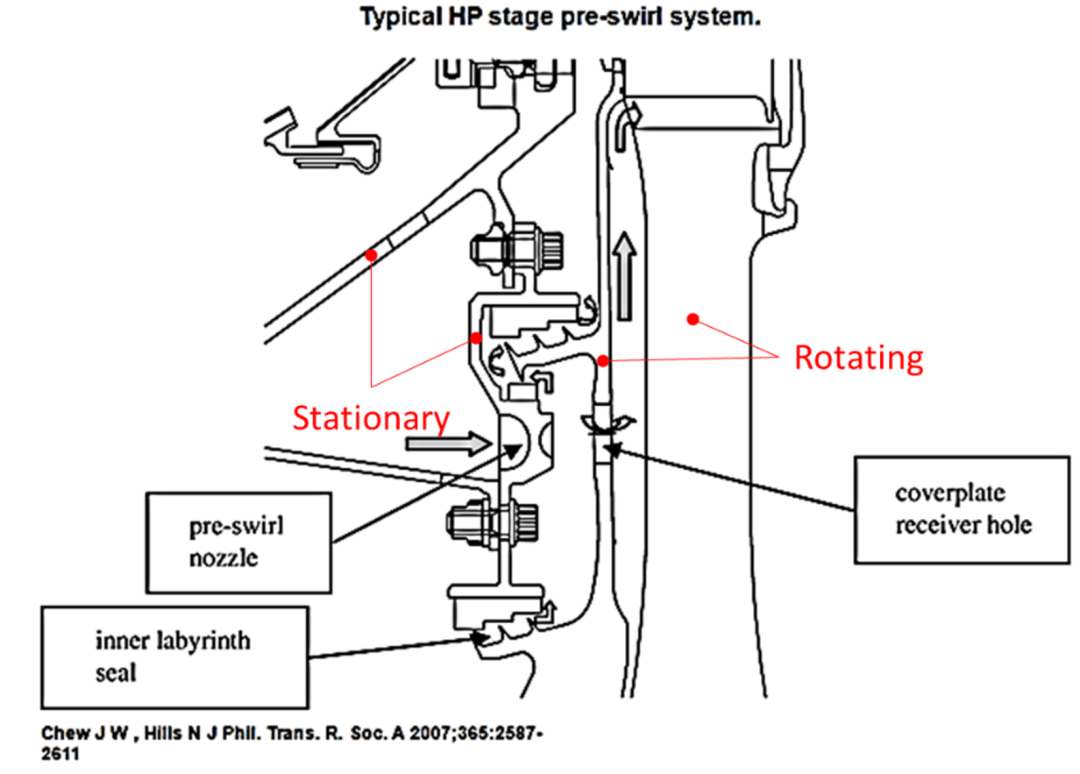
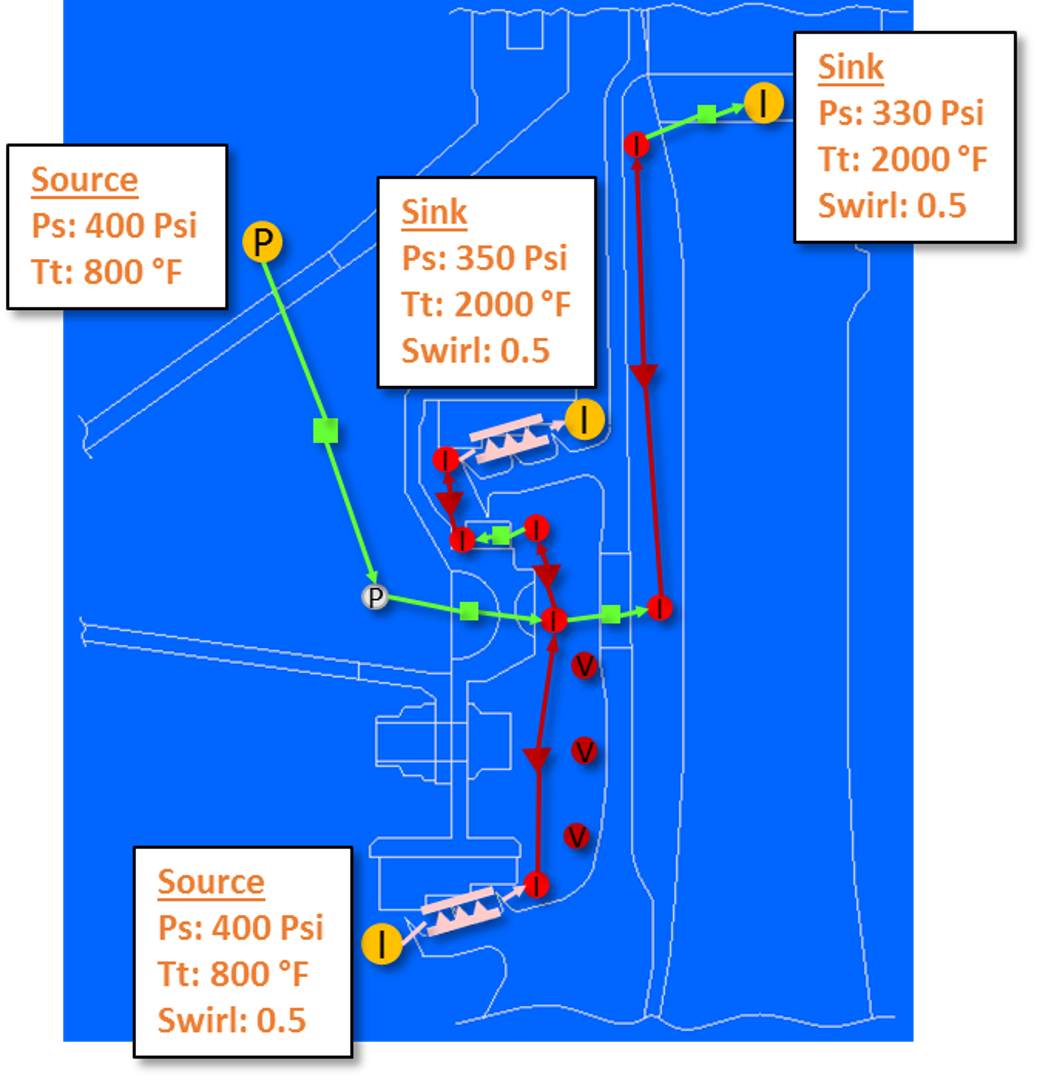
涡轮冷却原理图
涡轮冷却一维CFD模型
HyperStudy 中的最小二乘回归模型是多项式表达式,它将输出响应与设计变量相关联。需要选择合适的Fit算法才能创建准确的近似值。这要求事先了解输出响应的行为(线性、非线性、噪声等),并且需要足够的DOE样本点来达到回归分析的精度。
R-Square表明Fit的精度,值越高Fit的质量越好。例如,如果 R-Square = 0.84,则数据中 84% 的方差可通过Fit预测。高于 0.92 的值通常非常好,低于 0.7 的拟合精度较差。

HyperStudy中定义设计变量和响应

HyperStudy中定义DOE方法
Fit工具给出一个三次样条函数, y=A+Bx+Cy+Dx^2+Ey^2+Fx^3+Gy^3 来表达响应值和2个输入参数的关系。

得到回归方程式




