基于某实例的显式、隐式动力学算法差异对比
1. 前言
在进行非线性动力学计算中,比如接触问题、材料非线性问题、几何非线性问题,大部分(默认算法)还是使用隐式动力学算法(以下简称隐式算法)。隐式算法把分析过程划分成一系列的增量步,在每个增量步内进行多次迭代,得到满足精度的解后,再求解下一个增量步。虽然隐式算法能解决大部分非线性问题,但是在一些问题中也暴露了它的弊端(本文会清晰揭露)。最初发展显式动力学算法(以下简称显式算法)就是为了分析那些隐式算法分析极端费时的高速动力学问题,比如子弹高速击穿钢板时钢板的响应、圆桶内部瞬时爆炸时桶壁的响应,等等。需要指出的是,隐式算法、显式算法都具有解决问题的能力,没有孰优孰劣,从两者出现的时间来说,显式算法应该是对隐式算法的一种补充。对于一个确定的实际问题,采用哪种算法需要综合考虑各种因素,如果对于两种算法都可以求解的问题,求解效率可能起着决定性的作用。本文针对同一个实例,分别使用显式、隐式算法来求解,来对比说明两者的差异。
2. 显式、隐式动力学算法简介
为了更好地理解显式、隐式算法的区别,可以通过查阅相关资料来理解两者的内在算法理论。本人通过查阅Abaqus帮助文档和网上相关资料,简单地整理了它们各自的算法理论。如果想更深入、更系统理解,需要查阅更多的资料,由于篇幅有限,只简单描述。
2.1 显式动力学算法
在Abaqus帮助文档中,详细介绍了显式算法的基本原理。

以上文档主要意思就是在增量步开始时根据动力学平衡条件得到加速度,得到加速度后,在时间上“显式地”得到前推速度和位移。“显式”是指在增量步结束时的状态仅仅依赖于该增量步开始时的状态(位移、速度、加速度),在这个过程中,假设加速度是恒定的,因此要求时间增量要足够小(增量步要足够大)才能得到精确的结果。虽然显式算法是逐步向前推,不涉及迭代和解方程组,但是显式算法还是有条件稳定的,稳定的条件是增量步足够小。
2.2 隐式动力学算法
使用隐式算法计算某一增量步结束的状态时,不仅需要该增量步开始的状态,还需要使用该增量步结束的状态(与显式算法最主要的差别),需要联立非线性方程组迭代求解。具体可参考如下资料(摘自网址https://zhuanlan.zhihu.com/p/136573979?utm_oi=77416395440128)。

2.3 两种算法的对比
通过了解两种算法的理论,可知两者的主要区别如下两点:
(1)显式算法需要很小的时间增量步(因为只有在很小的时间增量步中,加速度才能近似看成是恒定的),它仅依赖于模型的最高固有频率,而与载荷的类型和持续时间无关,通常的模拟需要设置10000-1000000个增量步,每个增量步的计算成本较低。
(2)隐式算法对时间增量步的大小没有内在的限制,增量步的大小通常取决于精度和收敛情况。典型的隐式模拟所采用的增量步数目要比显式模拟小几个数量级。然而,由于在每个增量步中必须求解一套全域的微分方程组,所以对于每一增量步的计算成本,隐式算法远远高于显式算法。
3. 实例对比
为了清晰对比显式、隐式算法的差异,采用一个实例(子弹射击钢板,子弹设置为刚体,钢板为弹性体,对比结果为钢板的应力大小。为了简化问题,突出重点,不涉及材料塑性变形和损伤),分别使用以上两种算法,观察结果之间的差异。
3.1 显式算法
在设置分析步时,选择“动力,显式”分析类型,分析时长为0.0015s,打开几何非线性选项,控制增量步数量为10000次,则最大时间增量步设置为1.5e-7,其余默认设置,见图1。
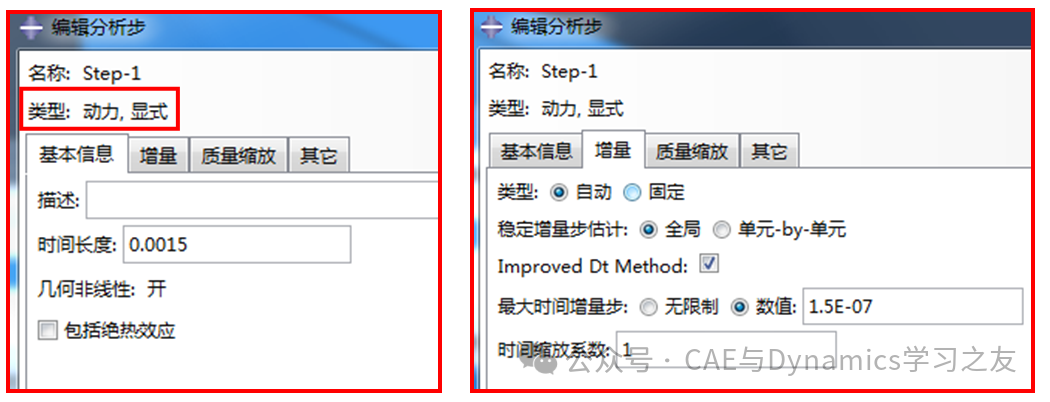
图1 分析步的设置
接触属性按默认设置,见图2。
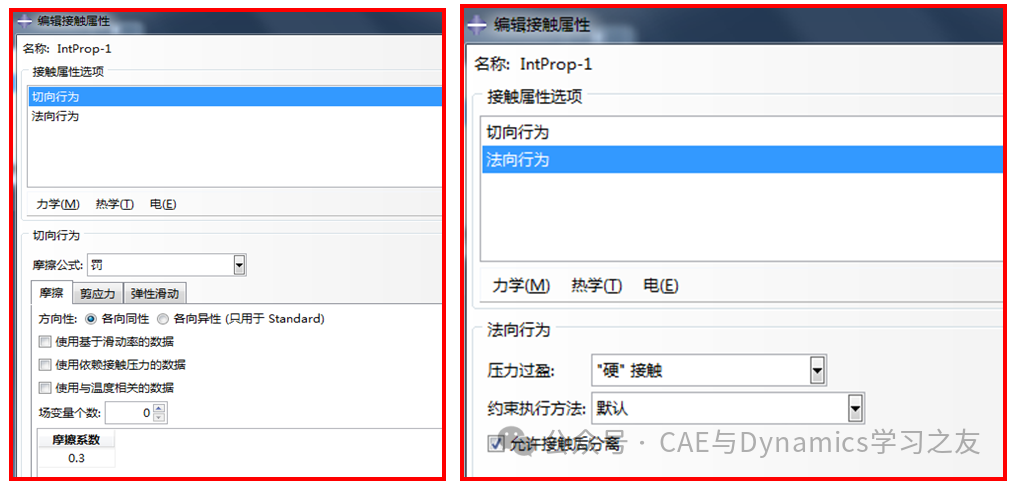
图2 接触属性
在定义相互作用时,使用面-面接触,选取子弹外表面为第一表面,钢板所有节点为第二表面,其余选取默认,见图3。
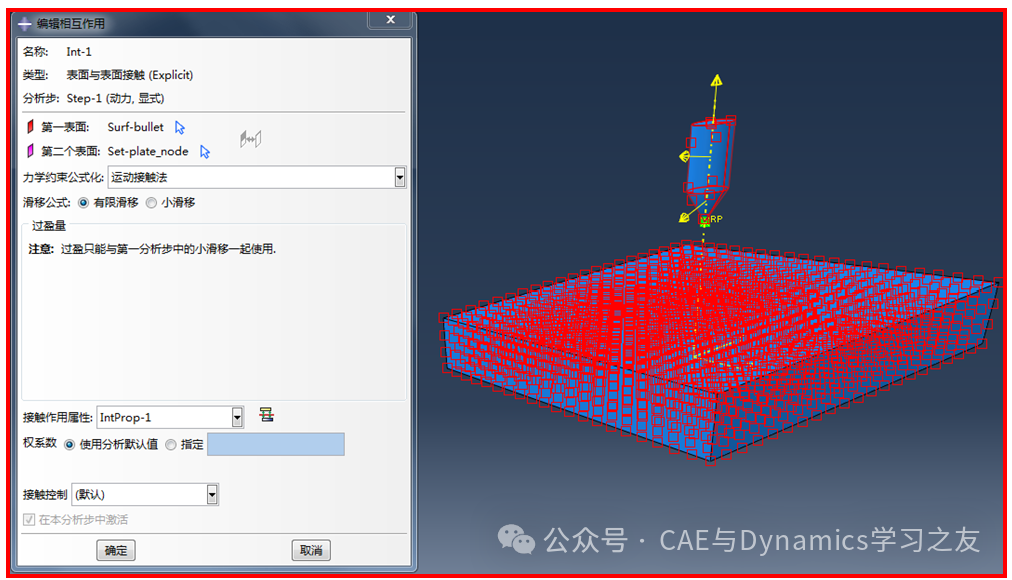
图3 接触面的选取
提交计算,结果见图4,共有10002个增量步,钢板应力最大发生在t=5.25e-4s时,此时,应力最大值高达7320Mpa。
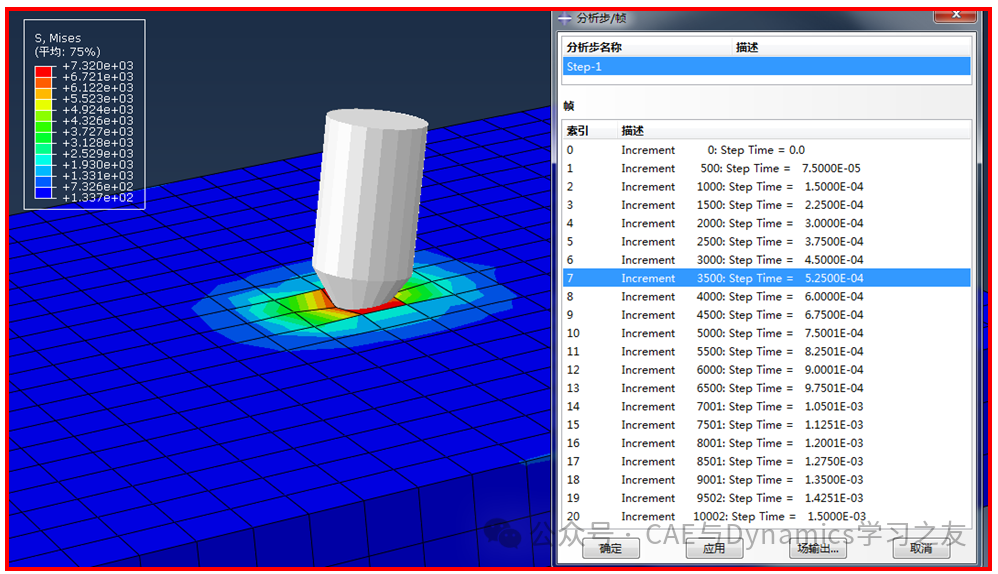
图4 显式算法计算结果
为了查看最大应力节点位置处的应力随时间(增量步)变化情况,按照图5方法创建XY数据显示。
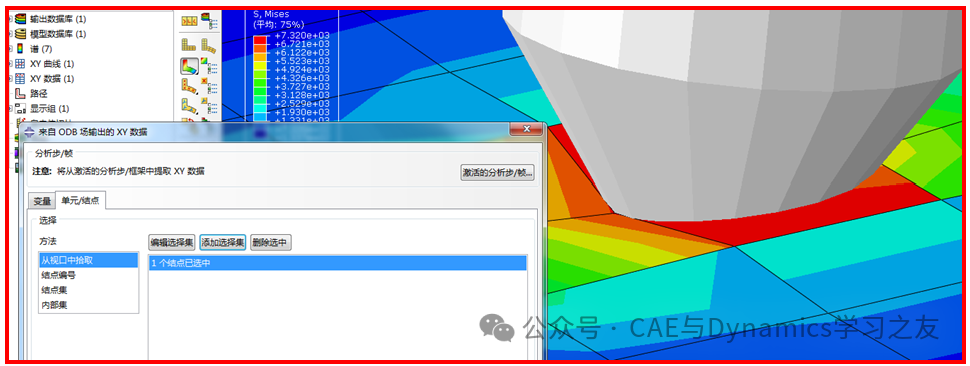
图5 创建XY数据显示
创建完成后,绘制出来,则最大应力节点位置处的Mises应力随时间(增量步)变化情况如图6所示。

图6 最大应力节点位置处的Mises应力时间历程
3.2 隐式算法
在设置分析步时,选择“动力,隐式”分析类型,分析时长为0.0015s,打开几何非线性选项,其余默认设置,见图7。
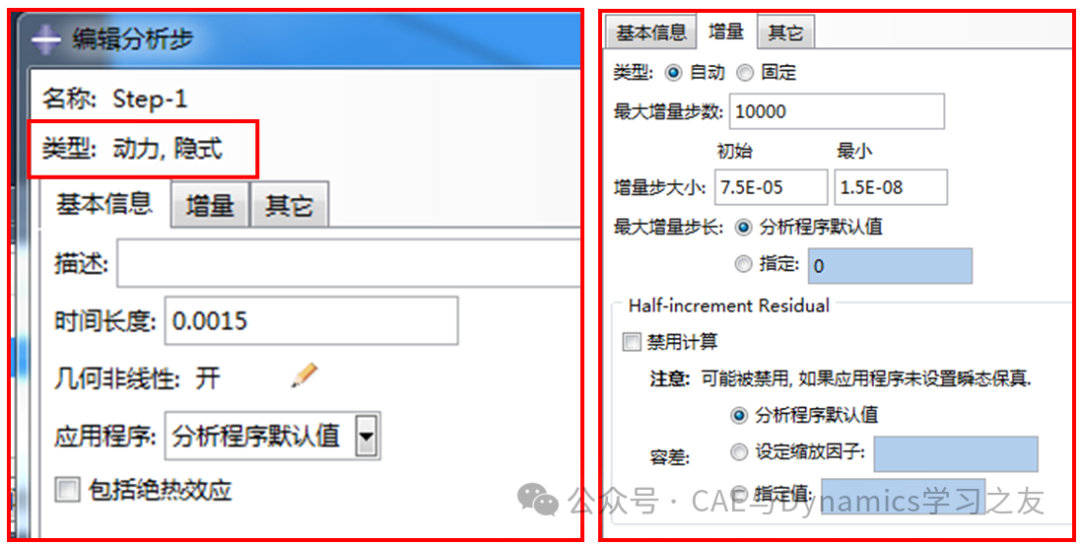
图7 分析步的设置
在隐式算法中,接触属性按默认设置,与显式算法一样,见图2。
在定义相互作用时,同样使用面-面接触,选取子弹外表面为主表面,钢板所有节点为从表面,其余选取默认,见图8。
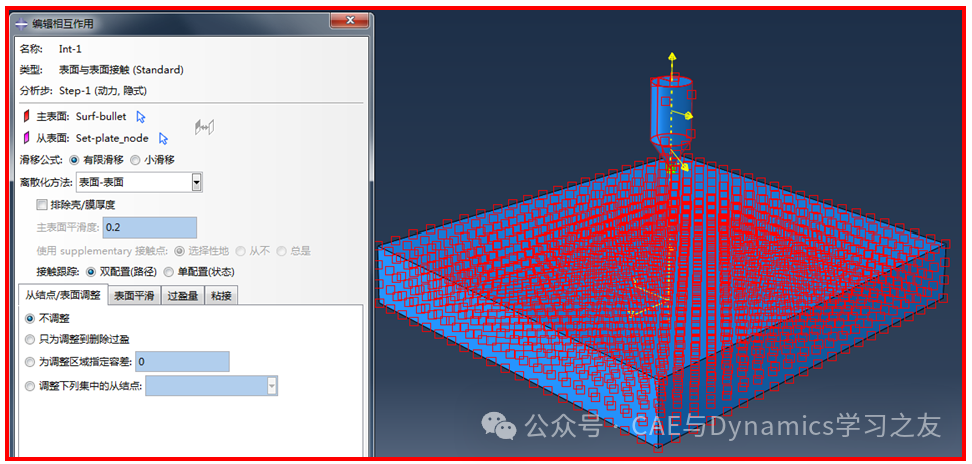
图8 接触面的选取
提交计算,结果见图9,只有26个增量步,钢板应力最大发生在t=5.82e-4s时,此时,应力最大值约为4874Mpa,比显式算法结果要很小很多(显式算法下最大值为7320Mpa)。
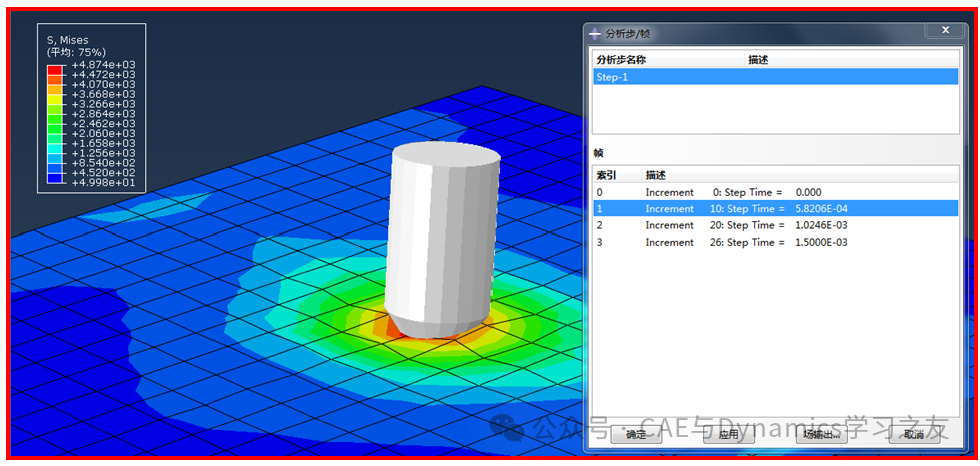
图9 隐式算法计算结果
在相同的节点位置创建应力时间历程,见图10所示。
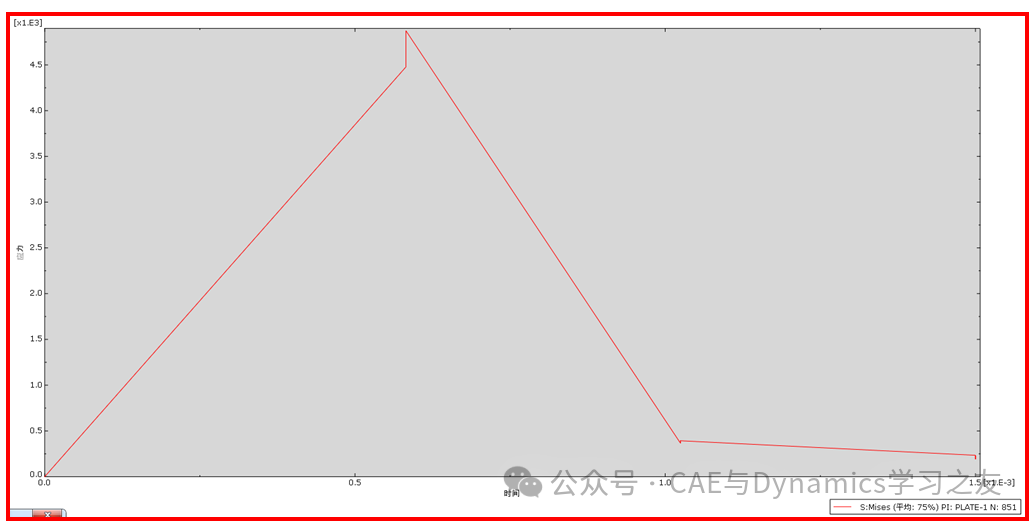
图10 最大应力节点位置处的Mises应力时间历程
对比图6和图10可知,使用显式算法能反映碰撞细节,使用隐式算法得到的结果不能反映细节,失去了在碰撞过程中钢板各个时间点的应力信息。那么有没有办法让隐式算法也能反映细节呢??答案是肯定的,那就把时间增量步固定为某个小值,比如把增量步设置为1.5e-7(与显式算法中最大增量步设置一致,见图1),如图11所示。
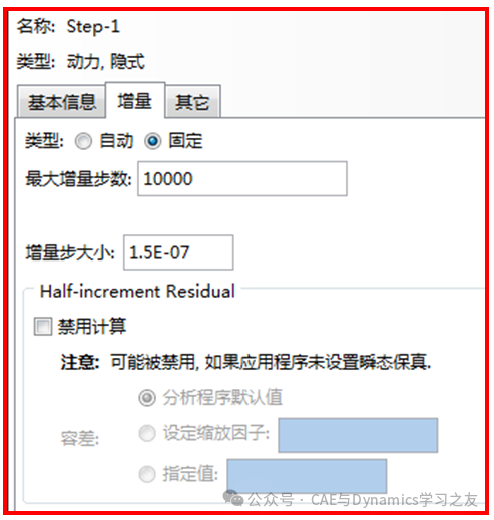
图11 隐式算法固定增量步
但是把时间增量步固定为小值会带来一个致命的问题就是计算时间太长,从提交到计算结束,整个过程花费了1小时13分钟35秒(结果见图12,可以反映碰撞细节),然而使用显式算法只花费了25秒(结果见图6),时间花费对比还是很震撼的,这也是显式算法出现的背景。
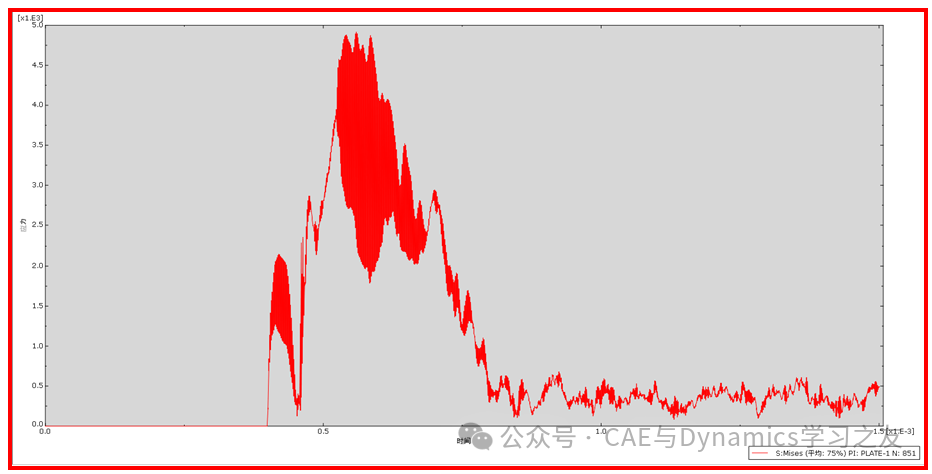
图12 最大应力节点位置处的Mises应力时间历程
END




