湍流模拟|19 近壁面处理
- 作者优秀
- 优秀教师/意见领袖/博士学历/特邀专家
- 平台推荐
- 内容稀缺
CFD 方法中的壁面处理是预测壁面剪切应力所必需的,在动量方程中的壁面单元中需要壁面力。壁面剪切应力是根据 j=1 点的速度 (可能还有

假设确实存在通用速度曲线,那么 CFD 有什么好处?假设近壁单元(j=1)的速度是已知的,例如从上一次迭代中得到的速度。由于第一个单元中心的位置也是已知的,粘度和密度也是已知的,因此可以将它们全部代入方程 (9.56)。唯一的未知数是摩擦速度
通用分布由不同部分组成。在非常靠近壁面的地方,湍流受到阻尼,速度分布是线性的(粘性子层)。在完全湍流的近壁层,速度分布呈对数形式(对数定律)。这两个区域之间有一个 "过渡层"。图 104 以对数图描述了两个平板边界层分布(雷诺数不同)。速度分布大致可划分如下:
线性层。0<y+<5且U+=y+
过渡层。
对数层。
对数曲线有两个常数:冯卡门常数,通常选择为
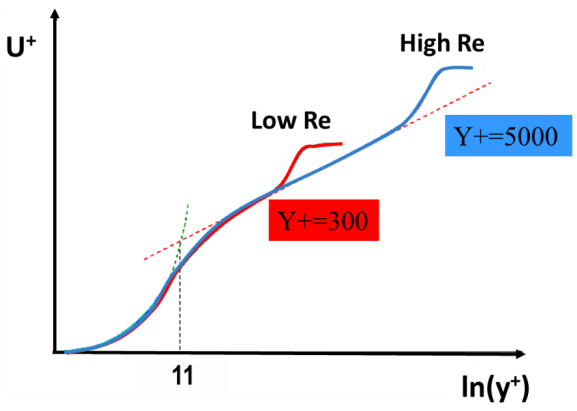
重要:虽然速度剖面在靠近壁面处遵循普遍规律,但以 y+ 为单位的对数层厚度取决于雷诺数。因此,对于高雷诺数流动,例如 y+ = 50 的 y+ 分辨率是足够的,但对于低雷诺数流动则不然。在高雷诺数情况下,壁面网格与边界层边缘(例如在
注意:即使是高 Re 数流动,内层(子层+过渡层+对数层)也只占整个边界层厚度的 10-20%。
”
1 标准壁面函数
一直以来,许多湍流模型都与壁面函数(Wall Function,WF)方法相结合。壁面函数不允许/不要求对粘性子层进行方程积分。相反,用户需要提供一套网格,其中第一层网格点(单元中心)位于对数层。然后根据对数层公式计算壁面剪切应力。具体的 WF 计算公式细节可以在文档中找到。
壁面函数处理法的优点是可以在相对较粗的网格(壁面法线方向)上进行模拟。但是,用户必须确保第一个层网格中心位于对数层中。如图 104 所示,这并非易事,因为对数层的上限取决于边界层分布的雷诺数。因此,对于对数层适用的位置,我们无法定义一个通用的上限。特别是对于中低雷诺数(设备雷诺数为 1e4 -1e6 ),对数层的厚度可能很窄,第一个网格点很容易被放置在离壁面太近或太远的地方,从而错过对数层。此外,在较低的雷诺数下,即使第一层网格中心位于对数层中,网格分辨率也可能不够,无法用足够的单元覆盖边界层的其余部分。
标准壁面函数存在很大问题,因为计算结果取决于用户的以下能力:
确保第一层网格中心点不要太靠近壁面,以免落入过渡层/粘性子层。 确保第一层网格中心点不要距离壁面太远,以免落入外层。 确保有足够多的网格解析边界层。
违反其中任何一个条件都会导致重大误差。最棘手的问题是,网格细化超过一定程度会导致结果恶化。这违背了数值方法的原则,即网格细化最终应导致更一致和网格收敛的解。上述要求很难实现,尤其是在低中雷诺数条件下。我们还不能忘记,网格是在求解之前创建的,因此将第一层网格放入对数层是一项艰巨的工作。因此,我们不鼓励使用标准壁面函数--基于
用户常常误以为壁面函数能处理边界层--也就是说,只需在网格中正确放置 y+ 近壁面网格,就能进行准确的边界层模拟。然而事实并非如此。壁面函数只是一种特殊类型的边界条件,边界层本身仍需要用足够多的网格来求解。
重要提示:使用标准壁面函数时,很容易因网格过粗或过细而产生不正确的解。因此不建议使用标准壁面函数。
”
重要:仅有适当的 y+ 并不足以进行精确的边界层模拟。边界层内还需要足够多的网格。
”
2 Scalable壁面函数
3 粘性子层模型(VSM)
一种更一致但更昂贵的方法是将方程一直积分到壁面上。这要求近壁面网格的分辨率为 y+~1 或更细。然而,只有在湍流模型被校准以表示子层的情况下,才能进行这种积分。由于湍流会受到过渡层和子层中粘性阻尼作用,大多数湍流模型需要额外的阻尼项和/或特定的边界条件才能考虑这种影响。
一直以来,可以积分到壁面的模型被称为低雷诺数模型或low-Re模型。这是一个极易混淆的术语,因为 "low-Re" 指的不是设备雷诺数,而是湍流雷诺数
为基于
鲁棒性差 取决于初始条件的多种解 未经数据校准的伪转捩行为 再附/滞止点/线的壁面剪切力和传热过大。
对此有一些补救措施。第一种也是应用最广泛的一种方法是使用所谓的 2 层公式([57], [58])。在这种方法中,
第二种方法是在基于
基于
重要:基于
”的模型比基于 的模型更难实现对壁面的积分。
4 Y+不敏感壁面处理
经典的 VSM 总是需要 y+~1 或更精细的近壁网格。在复杂的应用中,不可能对所有壁面都做到这一点。因此,最好能提供在 y+ 变化时保持一致的公式。这种模型称为 y+ 不敏感模型(或全 y+ 模型)。在一系列具有不同 y+ 分辨率的网格上计算流动时,此类模型可提供近似独立于 y+ 值的壁面剪切应力(和传热)水平。请注意,只有在边界层内有足够数量的网格时,这种说法才是正确的。在图 105 中可以看到采用这种公式进行的模拟,图中在三套不同网格上计算了平板零压力梯度边界层[29]。计算出的速度分布与细网格解密切相关。在 y+ > 20 的网格上,公式基本上切换回壁面函数。
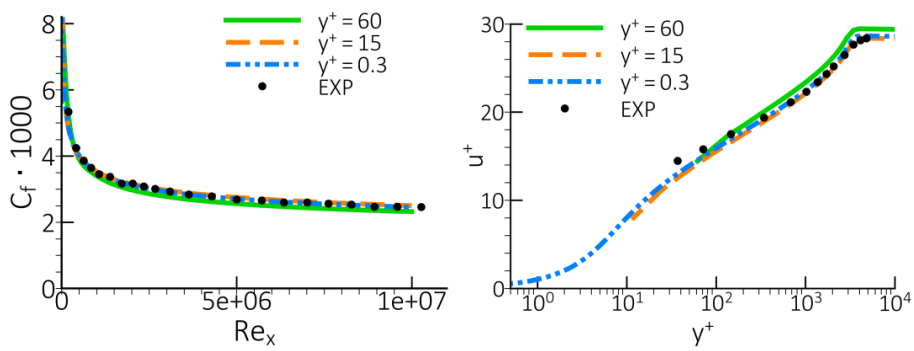
在 Fluent 中,Spalart-Allmaras 单方程模型和
4.1 基于w模型的y+不敏感近壁面处理
由于近壁面公式简单而稳健,无需复杂的阻尼函数(或像 V2F 模型那样的新的额外输运方程),因此
4.2 k-epsilon双层模型
为了避免历史上 VSM(low-Re)
在低雷诺数流动中,2L 混合可能会产生问题,因为在低雷诺数流动中,模型可能会被代数公式所支配。对于非平衡流动,2L 混合长度模型部分和
另一个问题来自于观察到的基于
这些例子表明,2L 模型的切换程序可能会产生问题。对于多相流和/或物理属性变化很大的复杂流动,情况更是如此,在这种情况下,模型会因混合长度和传输方程之间的不稳定切换而显示出不稳定性,从而阻碍求解器收敛。虽然 2L 公式在许多工业流中都能很好地使用,但它还不足以作为默认的湍流模型,因为默认的湍流模型需要适用于所有的物理场景组合。

注:系列译自《Best Practice: RANS Turbulence Modelingin Ansys CFD》,作者F.R. Mentor,2022
”
(完)




