文献分享——GPU加速的离散元模拟
文一:

基于GPU的颗粒系统DEM建模方法
DEM已被公认为研究颗粒物质基本原理的一种强大的数值技术。它在处理通常涉及数十亿个颗粒的实际颗粒系统方面的应用有限。图形处理单元(GPU)为这个问题提供了一个解决方案。本文探讨了基于GPU的DEM开发,并在各种条件下对其性能进行了评估。对于使用300000个球体的包装箱,证明了加速比(单个GPU与单个CPU)在40到75之间变化,这取决于所使用的并行算法。然后,基于GPU的DEM被开发用于涉及任意墙壁几何形状、移动墙壁边界和非球形粒子的其他系统。研究了高炉上料系统、螺旋输送机和转鼓中颗粒的流动规律。对于转鼓中的椭球体,当纵横比从1.0增大或减小时,动态休止角增大。还使用了具有消息传递接口(MPI)的多个GPU。结果表明,使用32个GPU的速度可以比单个GPU快18倍。它可以处理超过1000万个颗粒的大型颗粒系统。因此,本工作中开发的基于GPU的DEM使真实工业过程的模拟成为可能。
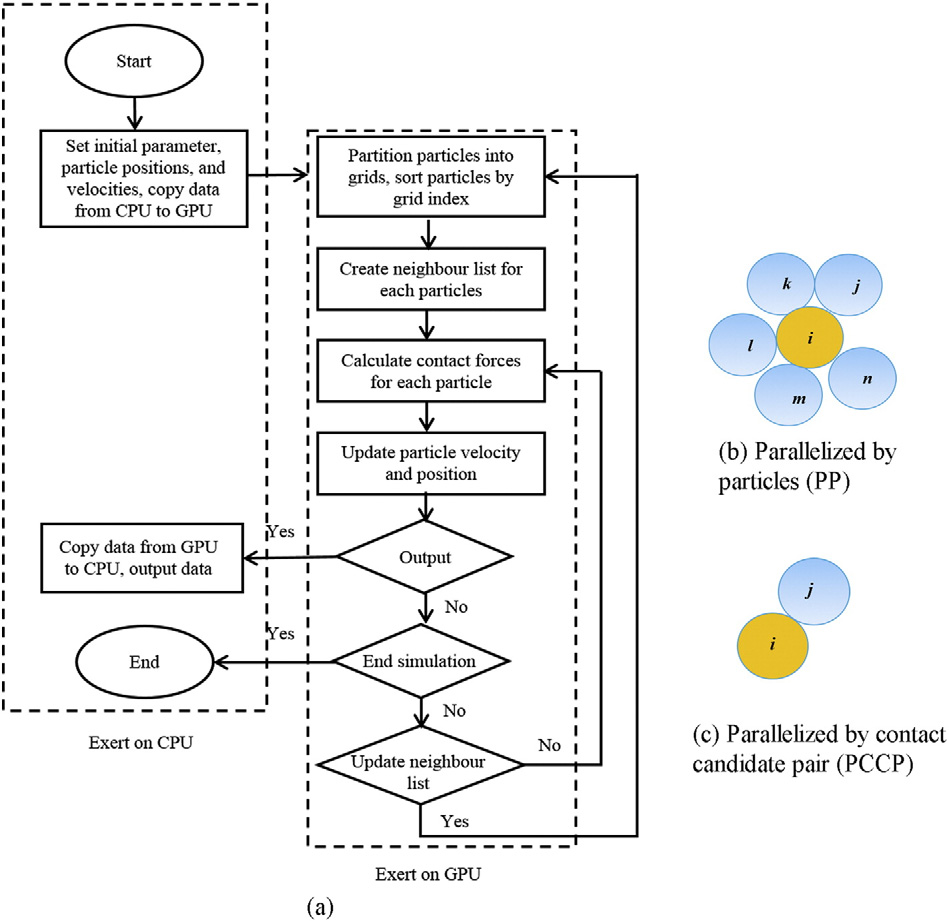
图:(a) GPU加速的离散元模拟流程图;(b)颗粒并行化计算;(c)接触并行化计算
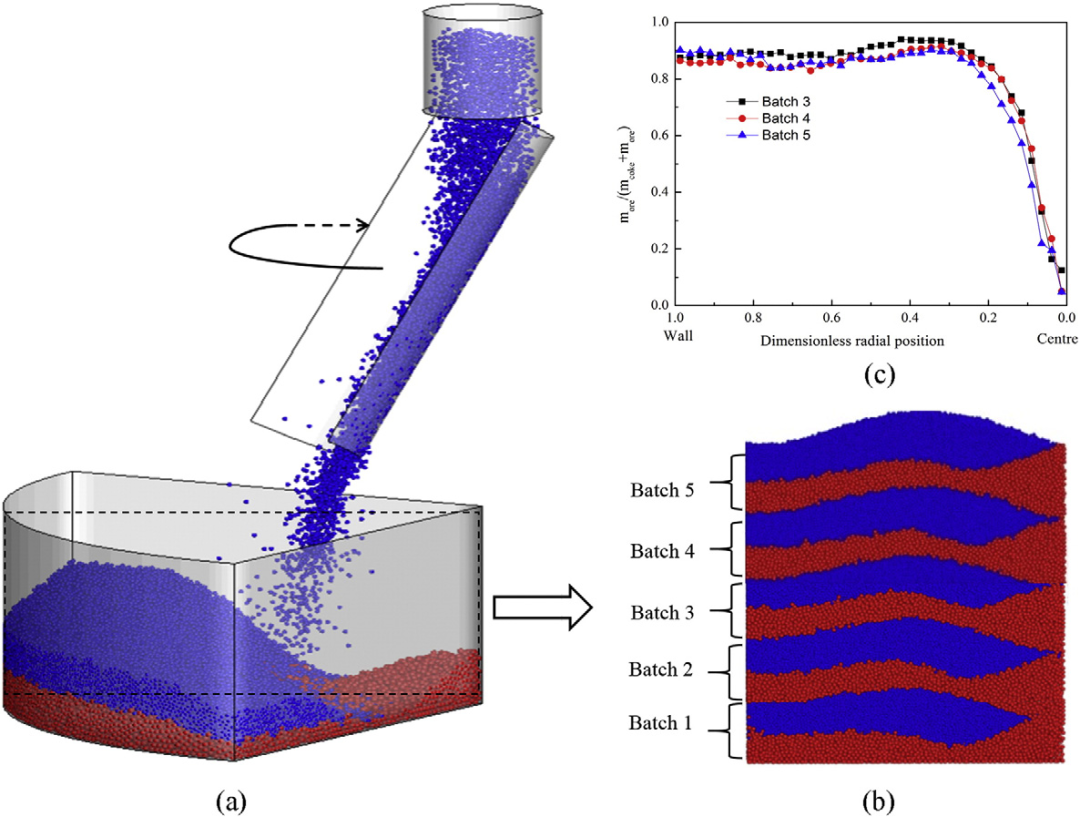
图(a)在炼铁高炉中使用旋转溜槽对炉料进行装料的过程,(b)5批装料后高炉中心槽的GPU结果(红色-粒度=55mm的焦炭,蓝色-粒度=30mm的矿石),以及(c)不同卸料批次中的模拟矿石/(焦炭+矿石)质量比
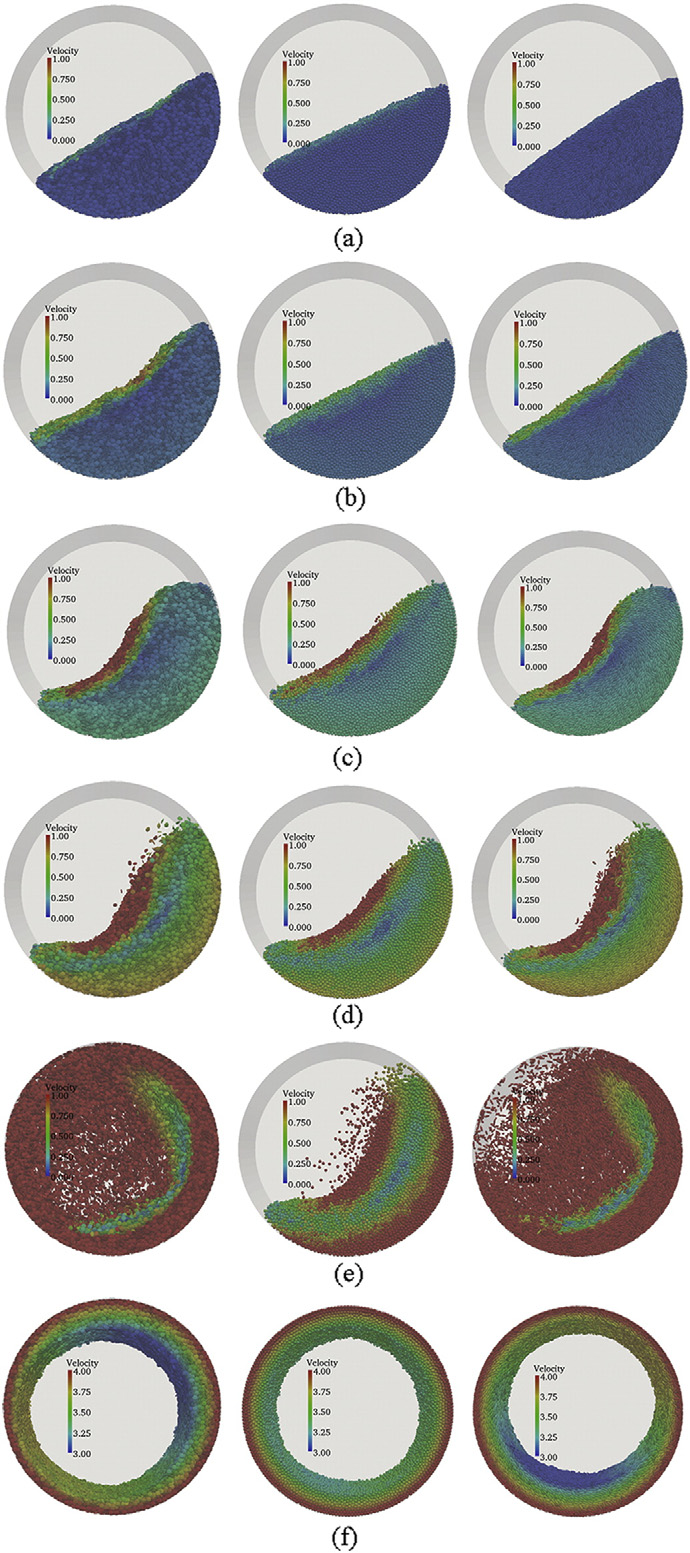
图:不同纵横比(左:α=0.25,中:α=1.0,右:α=3.0)和不同转速下的颗粒流模式:(a)rpm=1;(b) rpm=5;(c) rpm=15;
(d) rpm=40;(e) 转速=80;以及(f)rpm=200。颜色表示粒子速度,单位为m/s。

图:在(a)不同时间(rpm=600)和(b)不同转速(t=5.226 s)(根据颗粒指数着色)下,具有100万个颗粒的螺旋输送机中固体流中的颗粒流动模式。
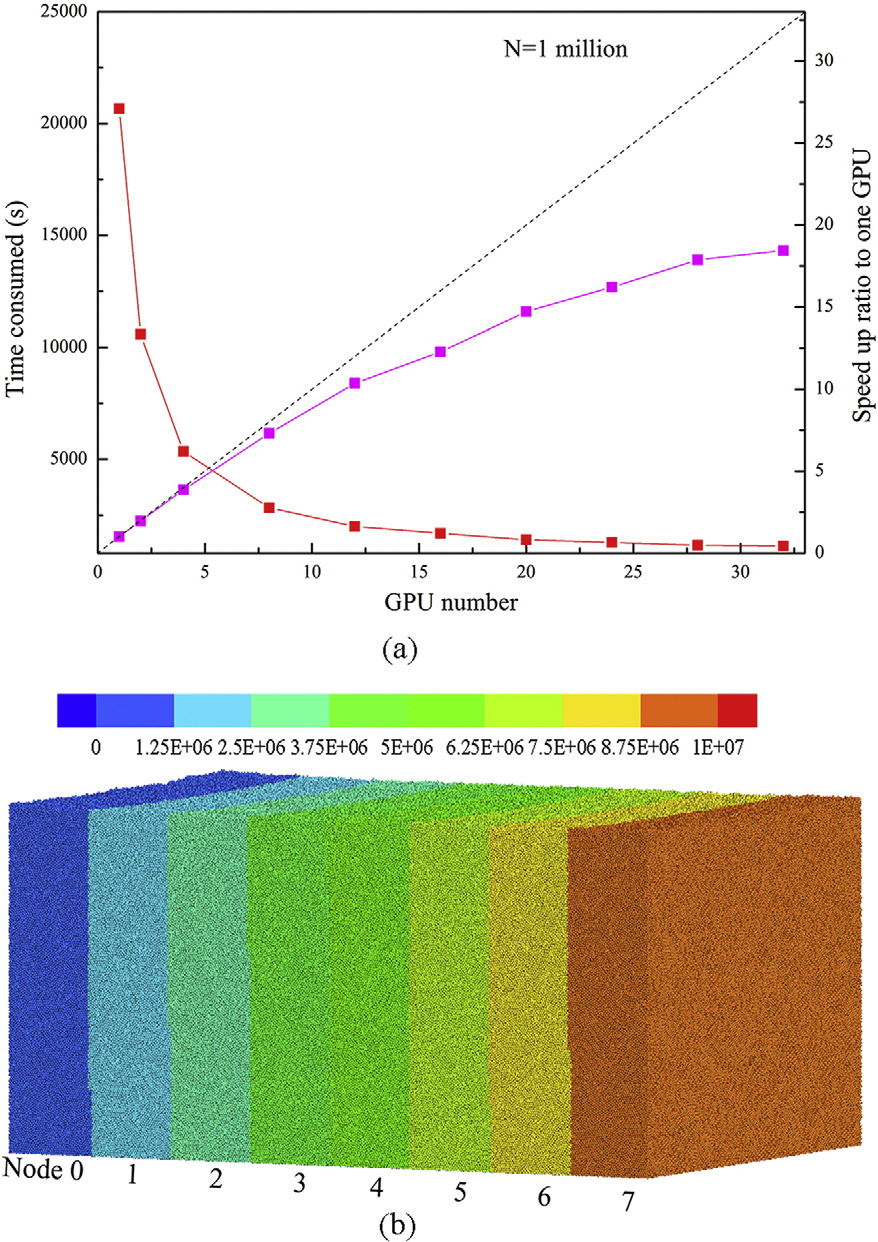
图:(a) 进程数量的加速比(与具有算法PP的单个GPU相比,粒子数量=100万),以及(b)使用8个节点和32个GPU将1000万个粒子的封装倒入一个盒子中。(按颗粒指数从0到107着色)。
文二:

基于GPU的DEM并行空间划分算法分析
求解岩土离散元法(DEM)应用的能力取决于模拟的复杂性及其计算要求。碰撞检测算法是有效解决数百万粒子之间机械碰撞的基础。这些算法是许多DEM应用程序的瓶颈,导致过多的内存使用或较差的计算性能。
特别是,对于基于GPU的DEM,用户在决定算法时需要考虑许多因素。
本研究讨论了一组不同类别的岩土工程问题以及算法选择的影响。考虑了四个因素:i)世界域大小、颗粒数量和颗粒密度,ii)大小的多分散性,iii)时间演变和iv)颗粒形状。研究表明,对于球形粒子,宽相位碰撞检测算法的选择对计算性能的影响最大。凸多面体粒子的计算成本主要取决于粒子边界体积的选择及其相交测试,而不是宽相位碰撞检测算法的选择。平均而言,对于凸多面体粒子,宽相最多占总运行时间的1.3%,而窄相碰撞检测和碰撞响应需要超过87%的运行时间。用作粒子边界体积的边界球体和轴对齐边界框的组合显示出最佳性能,将计算成本降低了20%。本研究为基于GPU的DEM碰撞检测及其在岩土工程中的应用提供了进一步的研究指导。
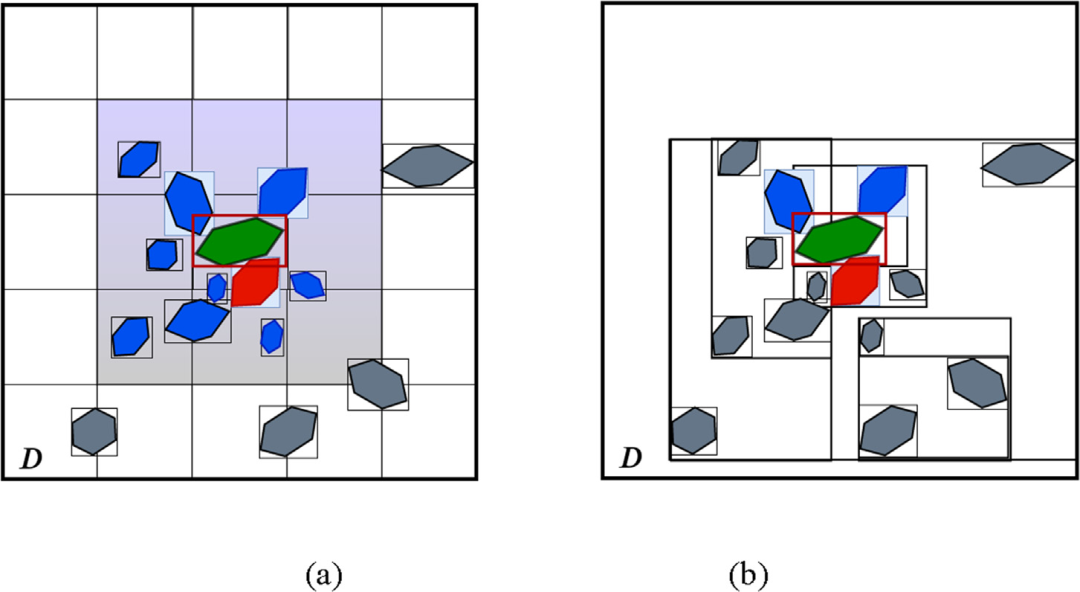
图:统一网格(a)和LBVH(b)空间滤波算法。显示的是具有候选粒子(绿色)、空间级邻居(蓝色)和接触(红色)的六边形多面体粒子。由蓝色框界定的粒子是通过强加的粒子边界体积标准找到的粒子的邻居。(关于本图例中颜色参考的解释,读者可参考本文章的网络版。)
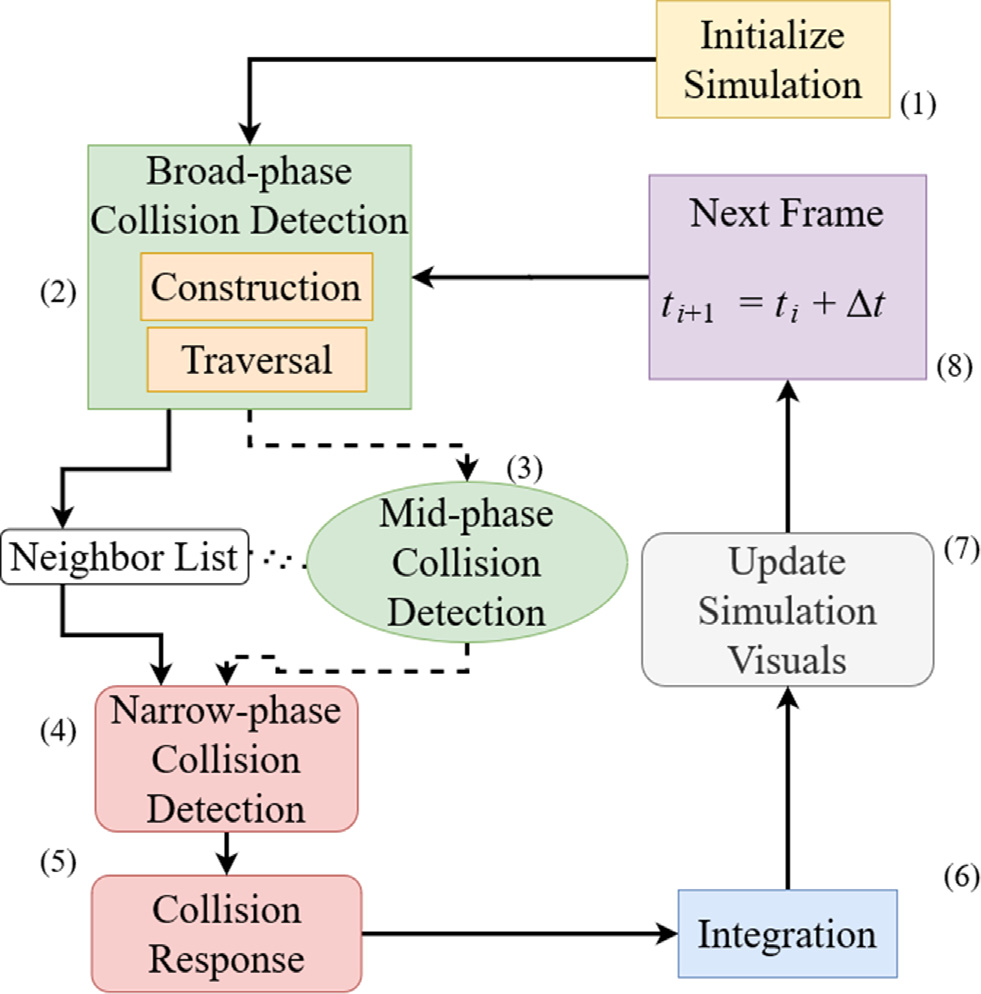
图:DEM模拟中的迭代图和编号阶段。

图:3D中粒子-边界体积相交测试的图示:(a)以x轴为界的边界球体(BS)之间的相交;(b) 轴对齐边界框(AABB)之间的交叉点;(c) 分离超平面之间的交集。这些标准按照计算成本从(a)到(c)进行排序。

图:岩土工程DEM模拟(a)约100万个球形颗粒的铁路道碴的ode metric试验的3D DEM模型(Liu et al.,2020)和(b)7864个颗粒的滑坡诱发波浪灾害过程(Xu等人,2020)。
文三:

基于 GPU 的大尺寸粉末压实过程数字高程模型
在本研究中,我们开发了一种基于GPU的离散元方法(DEM),以应对与粉末压实建模相关的挑战,特别是具有宽尺寸分布的大型系统。在该模型中,提出了一种在GPU架构中专门设计的多网格搜索方法来进行并行邻居搜索。设计了一种内存布局,以确保对邻居列表和相关联系历史的联合内存访问。所提出的GPU实现能够实现三级并行,从单个GPU到计算节点内的GPU,再到跨节点的GPU。将该模型应用于粉末压实,模拟结果表明,该模型在计算效率和压实行为预测方面有显著提高。

图:接触球体j和摆动液体桥连接球体k作用在球体i上的力的示意图。
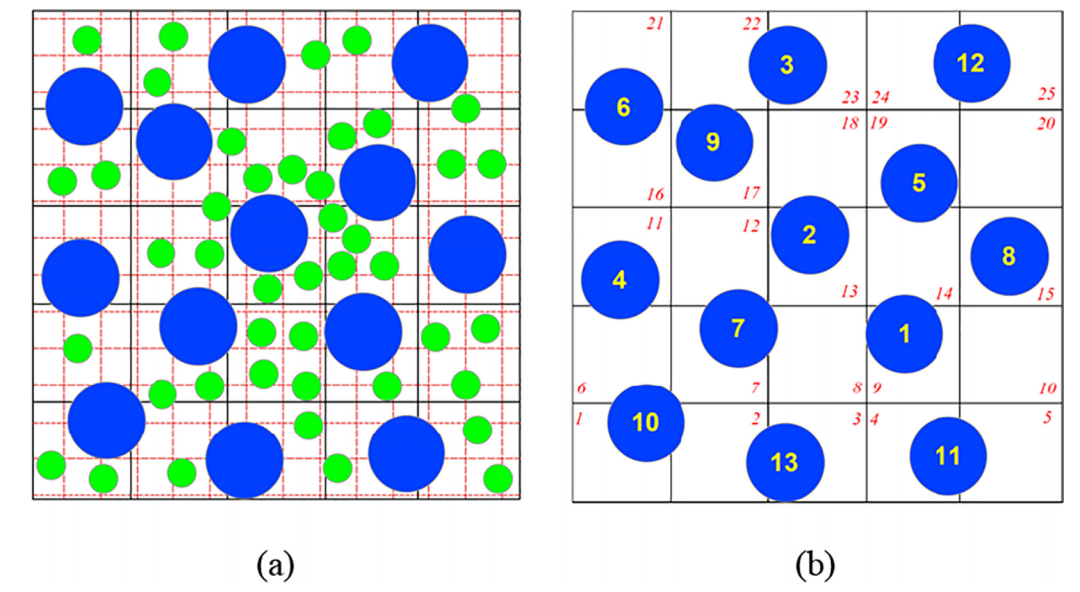
图:(a)搜索网格的两个级别的空间划分的示意图和(b)将大粒子映射到网格级别2中。
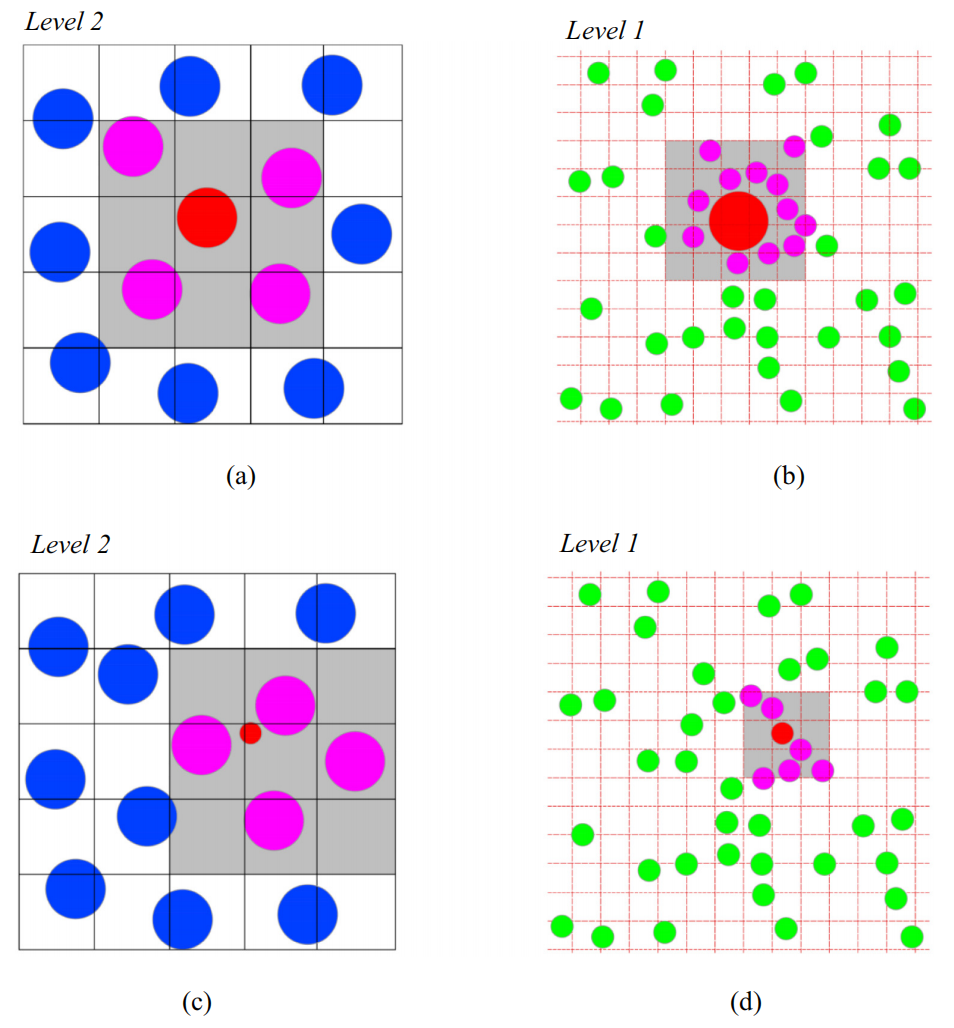
图:二元系统中邻居搜索算法的示意图,其中(a)电网级2上的大到大接触,(b)电网级1上的大至小接触,(c)电网级2中的小到大接触和(d)电网级一上的小到小接触。

图:(a) 失效模式和(b)具有不同压块长宽比的压块的键断裂演变。
文四:

基于GPU的自由表面颗粒-流体流动SPH-EM耦合方法
在许多工业过程中,如湿法球磨、浆料输送和混合,通常会遇到具有自由表面的颗粒流体流动。准确预测这些系统中的粒子行为对于建立对过程的基本理解至关重要,然而自由表面的存在使对它们的建模成为大多数传统的连续多阶段方法的挑战。光滑粒子流体动力学与离散元法(SPH-EM)的耦合有可能成为实现这一目标的有效数值方法。然而,由于计算要求高,该方法的实际应用仍然具有挑战性。在这项工作中,开发了一个完全在图形处理单元(GPU)上运行的通用SPH-EM模型来加速模拟。流固耦合基于局部平均技术,为了加速邻居搜索,双网格搜索方法适用于GPU架构,以解决SPH和DEM之间搜索区域的大小差异。模拟结果与自由面流和颗粒流溃坝的实验结果在定性和定量上进行了比较,验证了所建立模型的有效性。使用双精度浮点运算,可以在单个GPU上模拟1000多万个流体粒子。对于单相和两相流,都获得了计算时间随颗粒数量的线性可伸缩性。通过对搅拌管式反应器和转鼓的模拟,证明了所开发模型的实际应用,表明了其在处理涉及自由表面和颗粒-流体相互作用的复杂工程问题方面的能力。

图:SPH计算中使用的边界处理:边界粒子同时充当虚拟流体粒子和排斥粒子。
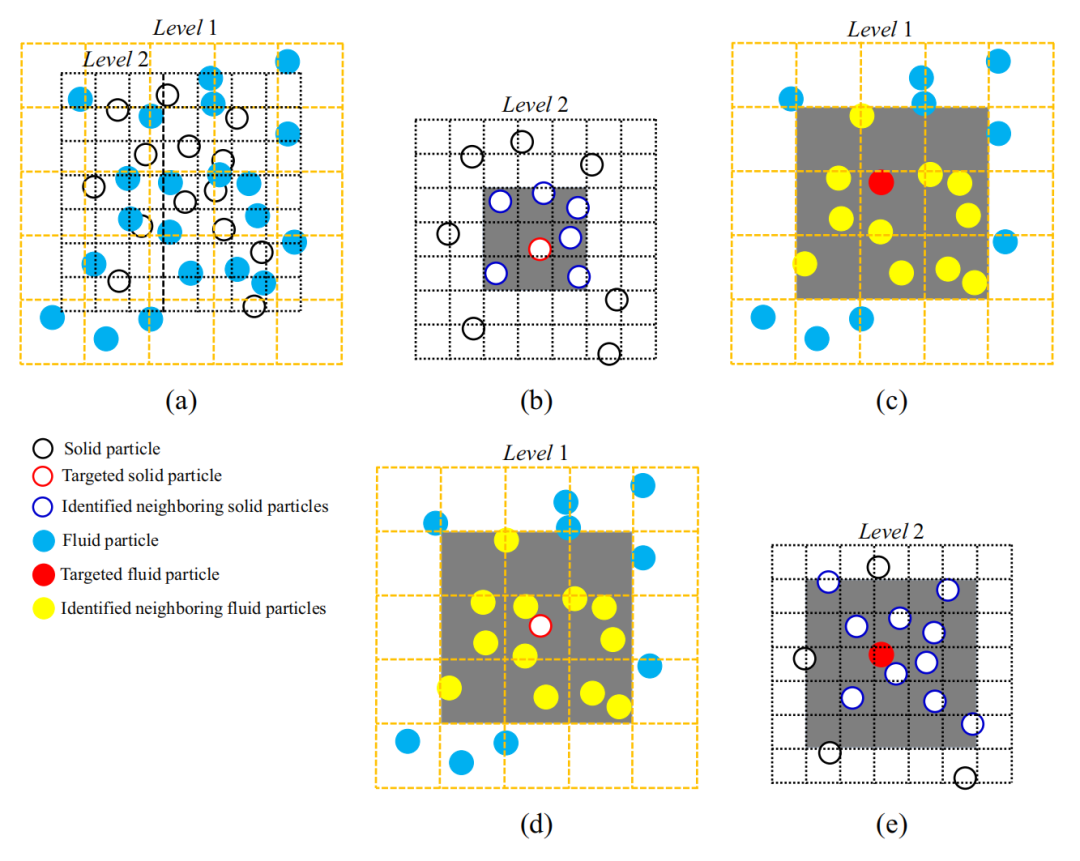
图:.图解说明了耦合SPH-DEM方法中使用的邻居搜索算法,其中(a)双网格系统,(b)在DEM网格中搜索固体邻居中的固体粒子,(c)搜索流体邻居中的流体粒子,(d)搜索液体邻居中的固体粒子和(e)搜索固体邻居的流体粒子。
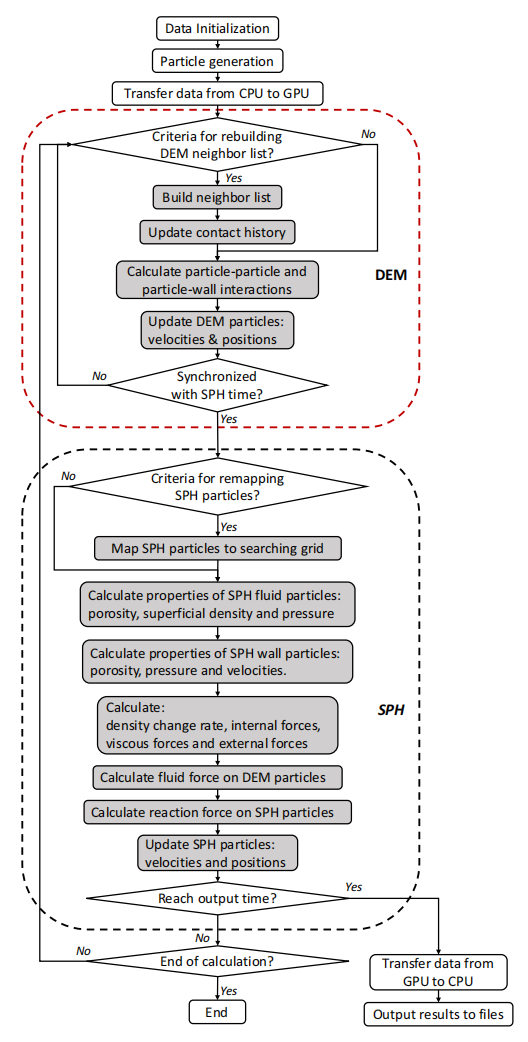
图:SPH-EM耦合方法的算法流程图。阴影框中的步骤是在GPU上执行的。

图:半填充ATR系统中不同相位的速度分布,其中相位a=0.581π,B=0.906π,C=1.150π,D=1.393π和E=1.637π。流体颗粒由管参考系中的速度大小着色。
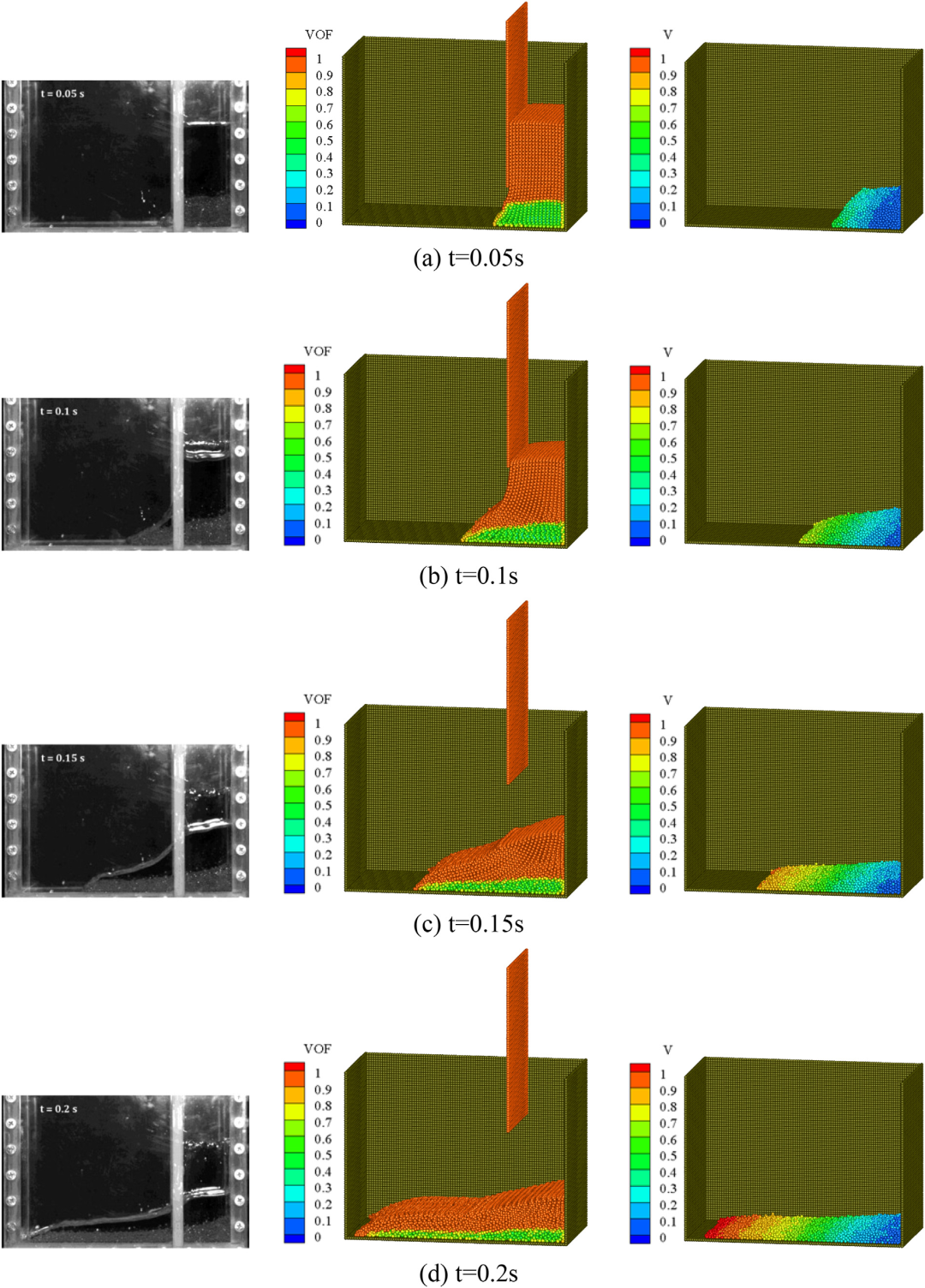
图:不同时期两相溃坝流态的比较: 实验[6](左)、流体相(中)和固相相(右)。




