拓扑优化:材料设计与计算固体力学的交叉课题
文一:

进化结构优化
摘要:
近年来,有限元分析(FEMA)已成为许多学科的工程师广泛使用的工具。然而,尽管优化理论和相关算法在过去三十年中取得了非凡的进步,但结构优化在实践中的受欢迎程度要低得多。这种情况至少部分是由现有结构优化方法的困难和复杂性造成的。
这项工作试图通过引入一种完全不同的结构优化方法来弥合有限元分析和结构优化之间的差距。它基于从结构中缓慢去除(或转移)低效材料的简单概念,从而使结构的最终形状朝着最佳方向发展。我们称之为进化结构优化(ESO)。
ESO方法适用于一系列结构设计问题,包括静力学、动力学和屈曲。与其他结构优化方法相比,ESO由于其简单有效而极具吸引力。任何具有有限元基本知识的人都可以很容易地理解和应用ESO方法。这本书是为对结构设计感兴趣的工程师和研究人员写的,包括学术界和工业界。他们的学科包括土木工程、机械工程和航空工程。这本书中包含的材料也会引起生物学家、医学从业者和其他对骨骼、树木和贝壳等自然载荷载体形状感兴趣的人的兴趣。
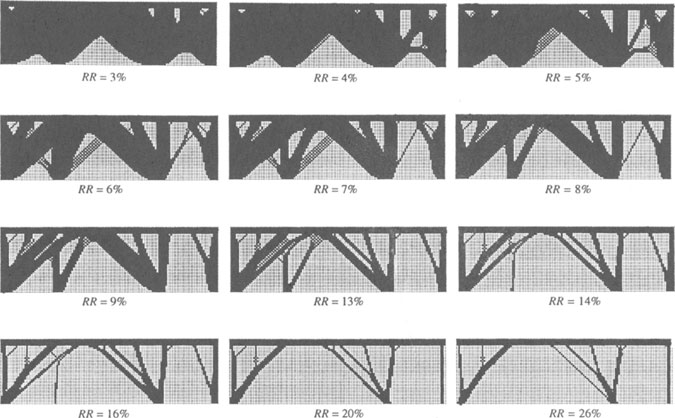
图:双支撑拱结构的 ESO 解决方案。

图:带有滚柱支撑的Michell型结构的ESO解决方案

图:极限条件下短悬臂的最佳设计:(a)0.50 mm;(b) 0.75毫米;(c) 1.00毫米。
文二:

双向进化结构优化方法的收敛性和网格无关解
摘要:
针对拓扑优化问题,提出了一种改进的双向进化结构优化方法。通过有限元分析计算出元素灵敏度数,然后将其转换为设计域中的节点灵敏度数。引入了一种使用节点变量的网格无关滤波器,以确定元素的添加,并在设计中消除一定长度尺度以下不必要的结构细节。为了进一步增强优化过程的收敛性,通过其历史信息提高了元素灵敏度数的准确性。通过求解几个柔度最小化问题证明了该新方法,并与惩罚固体各向同性材料(SIMP)方法进行了比较。结果表明,新的BESO方法在获得收敛解和网格无关解方面是有效的。

图:最初的设计(只有约30% 的设计领域的体积)

图:最终设计的10% 体积的设计领域: (a)等距视图和(b)前视图。

图:(a)无稳定性程序和(b)有稳定性程序的进化史比较
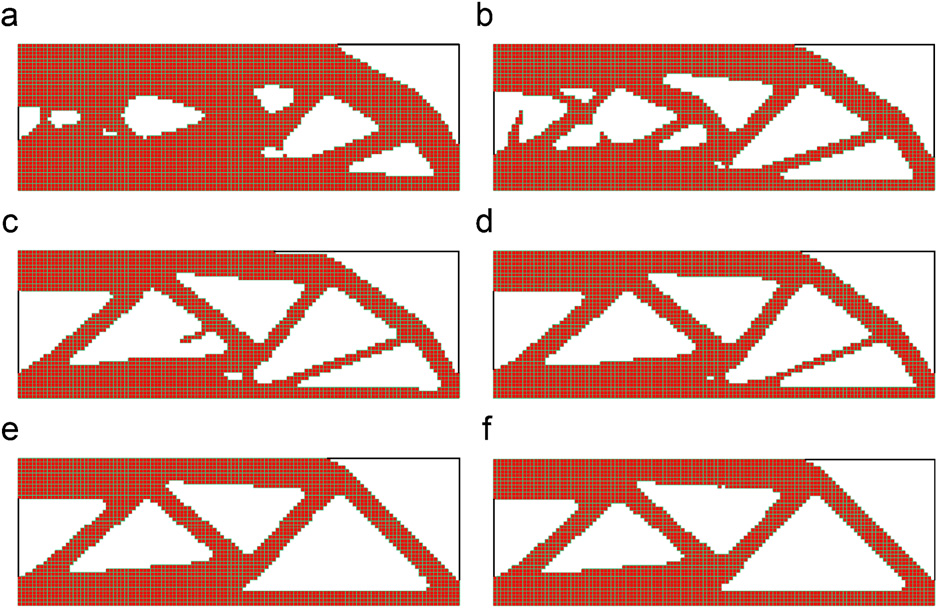
图:拓扑的演变:(a)迭代5,(b)迭代10,(c)迭代15,(d)迭代25,(e)迭代40和(f)最终拓扑。
文三:

一种或多种材料连续体结构的双向进化拓扑优化
摘要:
有几种公认的技术用于生成固体空隙优化拓扑结构,如固体各向同性材料惩罚(SIMP)方法和进化结构优化(ESO)及其后来版本的双向ESO(BESO)方法。利用材料插值方案,本文提出了一种新的带有惩罚参数的BESO方法。给出了一些例子来证明所提出的方法对于具有一种或多种材料的结构实现收敛最优解的能力。结果表明,目前BESO方法的优化设计与惩罚程度无关。所得到的最优拓扑结构和目标函数的值与SIMP方法的结果相比较。

图:设计区域
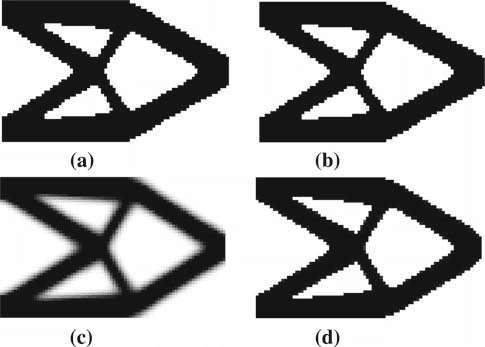
图:优化设计p=1.5的a BESO,p=3.0的b BESO,p=3.0的c SIMP和d的延拓方法
文四:

连续体结构的进化拓扑优化
摘要:
自20世纪80年代末以来,拓扑优化的理论、方法和应用取得了巨大进展。在拓扑优化的各种数值方法中,进化结构优化(ESO)和双向进化结构光学(BESO)已被世界各地的许多研究人员广泛研究。
谢和史蒂文于1997年出版了第一本关于员工持股的书。从那时起,该领域经历了快速发展,出现了各种新算法和越来越多的应用。
在过去的二十年里,几十位研究人员提出了许多不同版本的ESO/BESO算法。然而,文献中出现的一些算法不可靠且效率低下。本书的主要目的是对ESO/BESO,特别是BESO的最新技术和适当程序进行全面系统的讨论,以实现连续体结构的拓扑优化。
BESO方法适用于一系列结构设计问题,包括刚度和频率优化、非线性材料和大变形、能量吸收、多种材料、多种约束、周期性结构等。通过实例验证了该方法的有效性和对实际结构的适用性。
这本书是为对结构优化感兴趣的研究人员和工程师写的,包括学术和实践人员。他们的学科包括土木、机械、航空航天和生物医学工程。书中所包含的材料也将对寻求创造结构高效和美学创新的建筑和桥梁的建筑师有用。

图:基于不同单元去除率的集中荷载梁刚度优化 ESO 拓扑
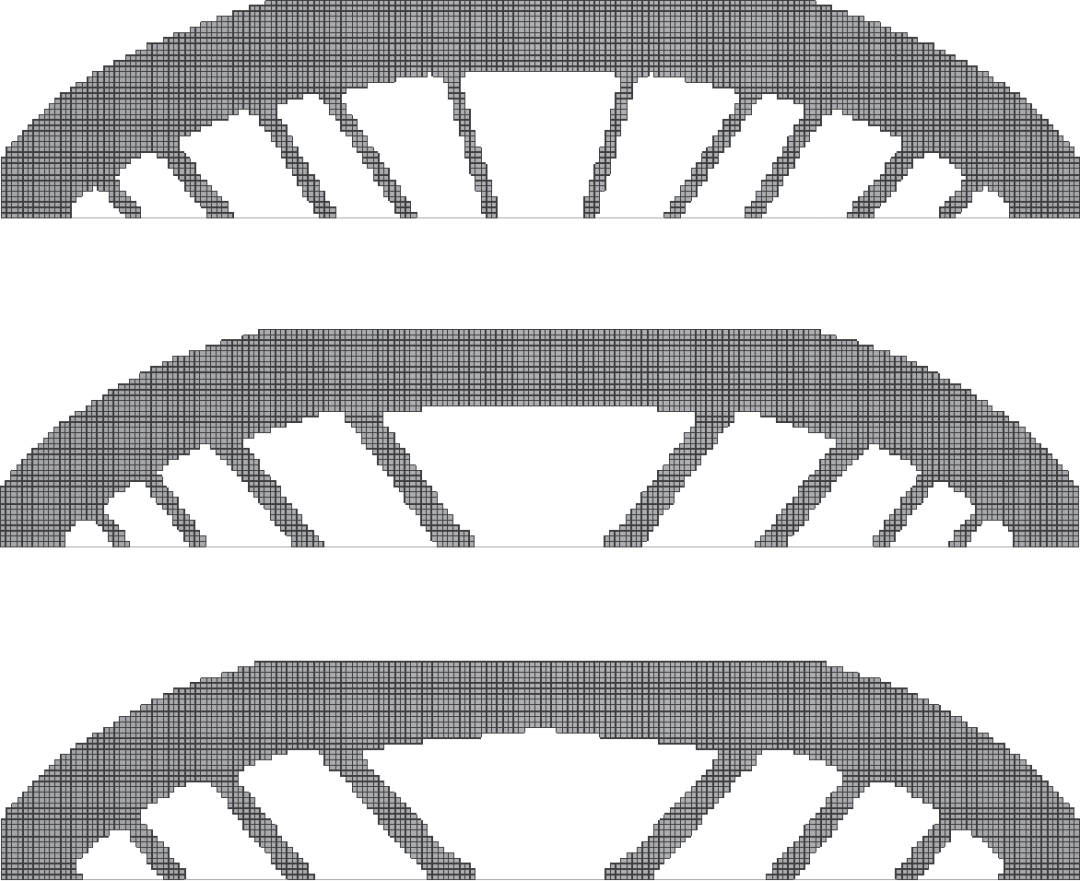
图:各种优化设计
文五:

结构优化的一种简单进化方法
摘要:
提出了一种简单的进化程序,用于结构的形状和布局优化。在演化过程中,低应力材料逐渐从结构中消除。给出了各种例子来说明通过这种程序实现的最佳结构形状和布局。

图:骨折中金属植入物的模型。

图:不同的材料减重下的优化方案




