PINN与机器学习求解偏微分方程
文一:

基于模型的迁移学习用于熔融传热分析的物理深度学习
摘要:
我们提出了一种基于物理深度学习的自适应深度配置方法(DCM),用于非线性热辐射运动表面上非牛顿(Sisko)流体的熔融传热分析。为了提高模型的计算效率和准确性,开发了拟合神经网络搜索(NAS)和基于模型的迁移学习(TL)。利用Buongiorno和非线性热辐射模型导出了边界层流动问题的控制方程。其次,引入相似变换,将控制方程简化为具有渐近无穷大边界条件的耦合非线性常微分方程。通过将物理约束纳入神经网络,我们使用所提出的深度学习模型来求解耦合的常微分方程。无穷大边界条件的施加是通过向损失函数添加不等式约束来实现的,向神经网络的超参数添加无穷大,该超参数在优化过程中动态更新。研究了各种无量纲参数对三种剖面(速度、温度、浓度)的影响。最后,我们通过几个数值例子证明了带迁移学习的自适应DCM的性能和准确性,它可以成为解决边界层问题的有前途的替代模型。

图:物理流模型示意图

图:迁移学习

图:纳米流体的速度、温度和浓度分布

图:考虑n=2有TL、无TL、n=3有TL和无TL的Sisko流体模型的收敛图
文二:

功能梯度材料三维瞬态传热分析的物理信息深度学习
摘要:
我们提出了一个基于物理的深度学习模型,用于采用Runge–Kutta离散时间方案的三维函数梯度材料(FGM)的瞬态传热分析。首先,给出了具有指数材料变化的FGM瞬态传热分析的控制方程、相关边界条件和初始条件。然后,介绍了用于瞬态分析的Runge–Kutta积分方案的深度配置方法。通过用离散时间方案和初始/边界条件约束温度变量,引入了有助于推广基于物理的深度学习模型的先验物理。进一步给出了适用于动态分析的拟合激活函数。最后,我们通过几个具有不规则形状和各种边界条件的FGM的数值例子验证了我们的方法。从数值实验来看,PIDL的预测结果与解析解和其他数值方法在预测温度和流量分布方面都很好地一致,并且可以适应不同形状FGM的瞬态分析,这可以成为瞬态动力学分析中有前途的替代模型。
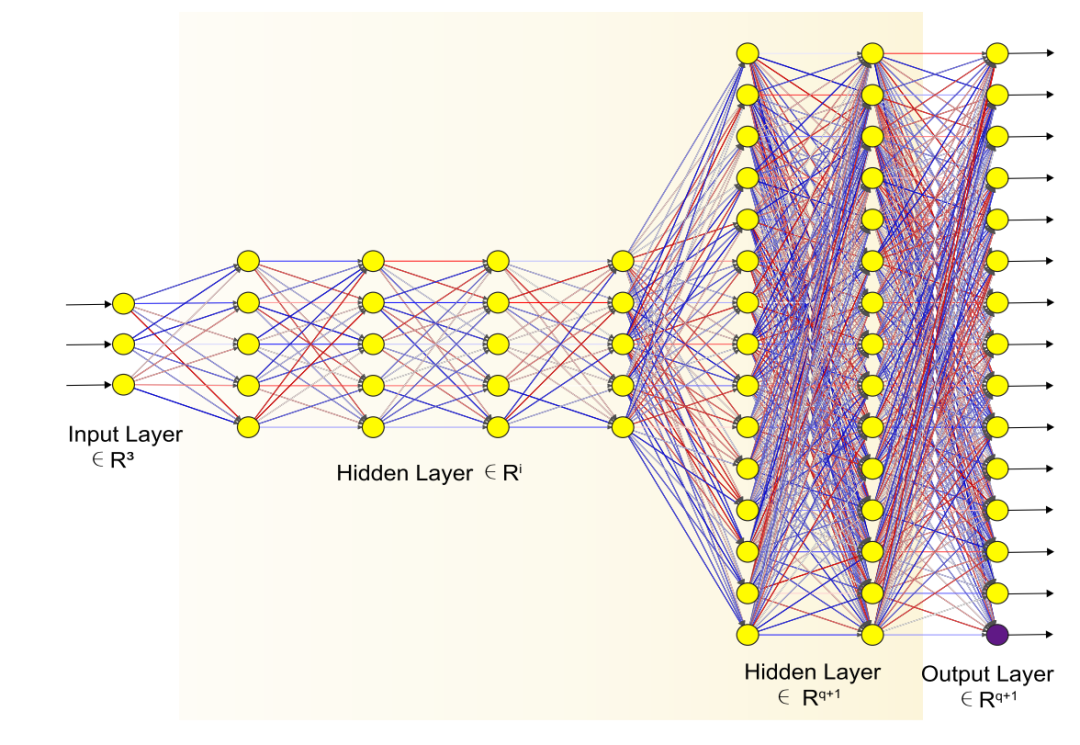
图:深度前馈神经网络的基本结构
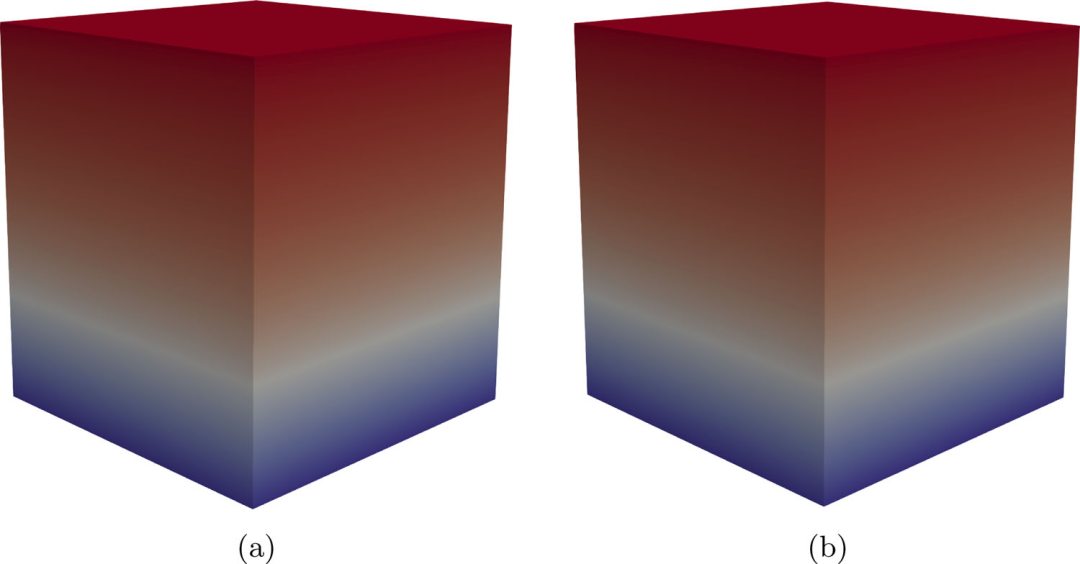
图:时间t=0.1s时功能梯度单位立方体的预测温度和b分析温度分布
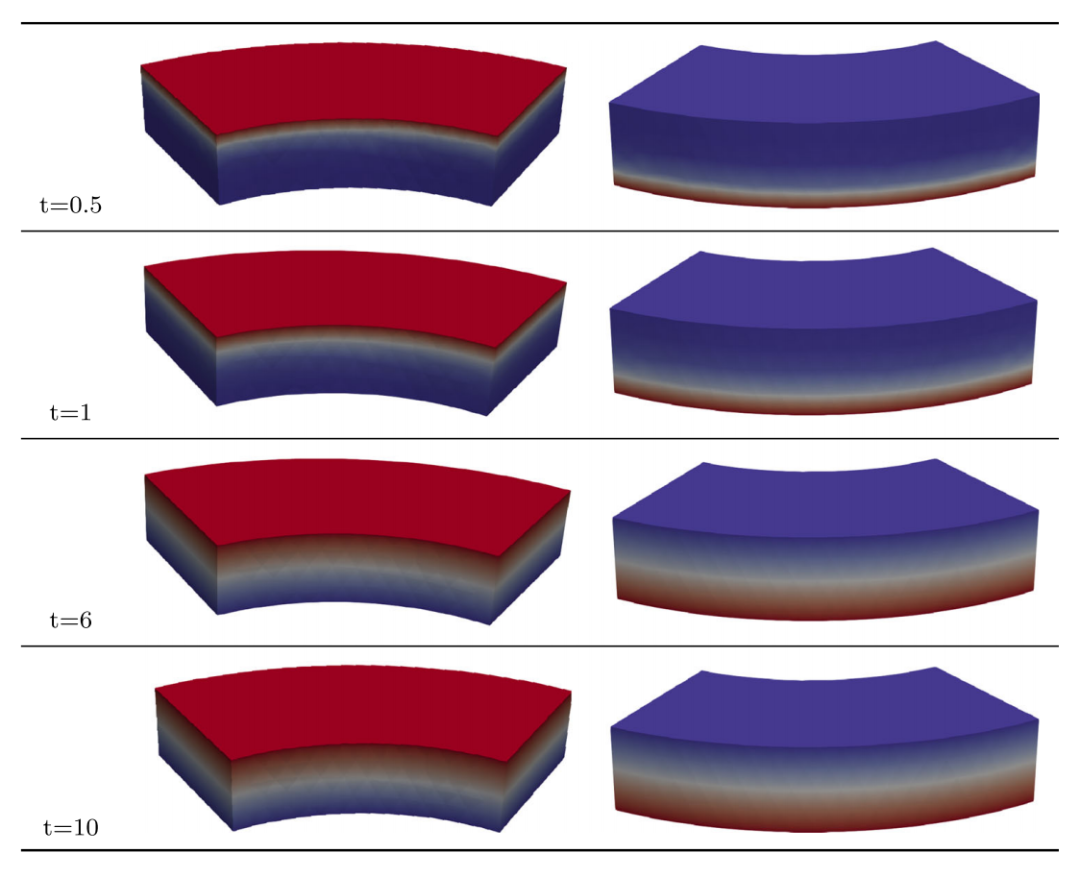
图:不同时间水平下不规则FGM的温度分布
文三:

力学特性的原子模型:机器学习原子间势的兴起
摘要:
自从2007年机器学习原子间势(MLIPs)概念诞生以来,为了进行更精确和可靠的分子动力学计算,用 MLIPs 代替经验原子间势(eIPs)已经引起了人们越来越多的兴趣。作为一个令人兴奋的新进展,在过去几年中,MLIP 的应用已经扩展到机械和失效响应的分析,提供了迄今为止无法有效实现的新机会,无论是 EIP 还是密度泛函理论(DFT)计算。在这篇小综述中,我们首先简要讨论 MLIP 的基本概念,并概述发展 MLIP 的流行策略。其次,通过考虑几个最近的研究实例,将强调 MLIP 在力学性能分析中的鲁棒性,并强调它们相对于 EIP 和 DFT 方法的优势。MLIP 还提供了惊人的能力,将 DFT 方法的稳健性与连续介质力学结合起来,使纳米结构的力学性能的第一原理多尺度模型在连续体水平上得以实现。最后但并非最不重要的是,基于 MLIP 的分子动力学力学性能模拟的共同挑战被概述,并为未来的研究提出建议。

图:用于共价块体材料纳米压痕模拟的原子环境动态学习
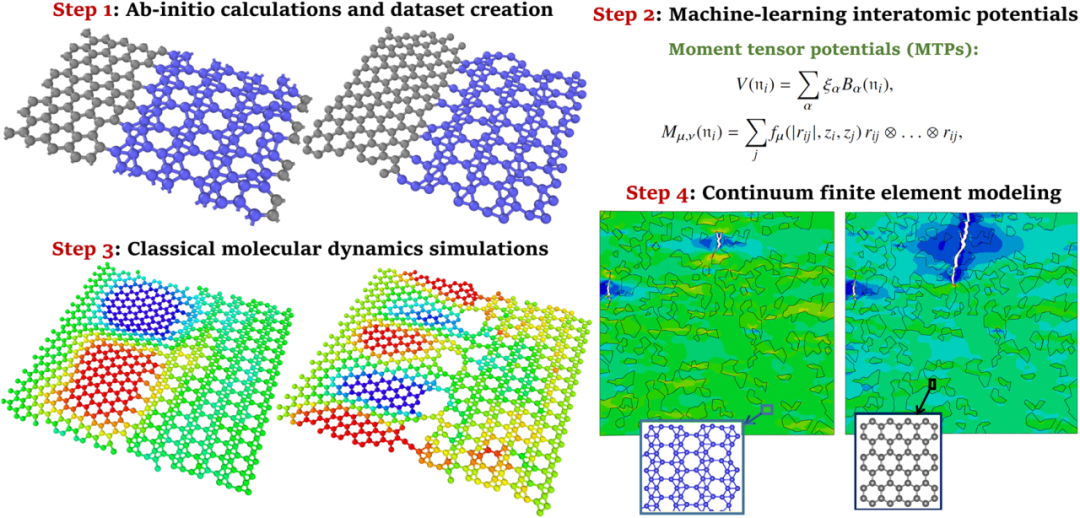
图:进行力学性能第一性原理多尺度建模的主要步骤
文四:

运用物理知识深度配置方法,利用材料迁移学习和敏感度分析分析非均匀介质中的三维潜在问题
摘要:
在这项工作中,我们提出了一种求解非齐次介质中三维势问题的深度配置方法。该方法利用具有材料迁移学习的物理信息神经网络,将非齐次偏微分方程的解简化为优化问题。我们测试了物理信息神经网络的不同配置,包括平滑激活函数、配置点生成的采样方法和组合优化器。将材料迁移学习技术用于具有不同材料等级和参数的非均质介质,增强了所提出方法的通用性和鲁棒性。为了确定网络配置中影响最大的参数,我们进行了全局灵敏度分析。最后,我们提供了DCM的收敛性证明。该方法通过几个基准问题进行了验证,还测试了不同的材料变化。
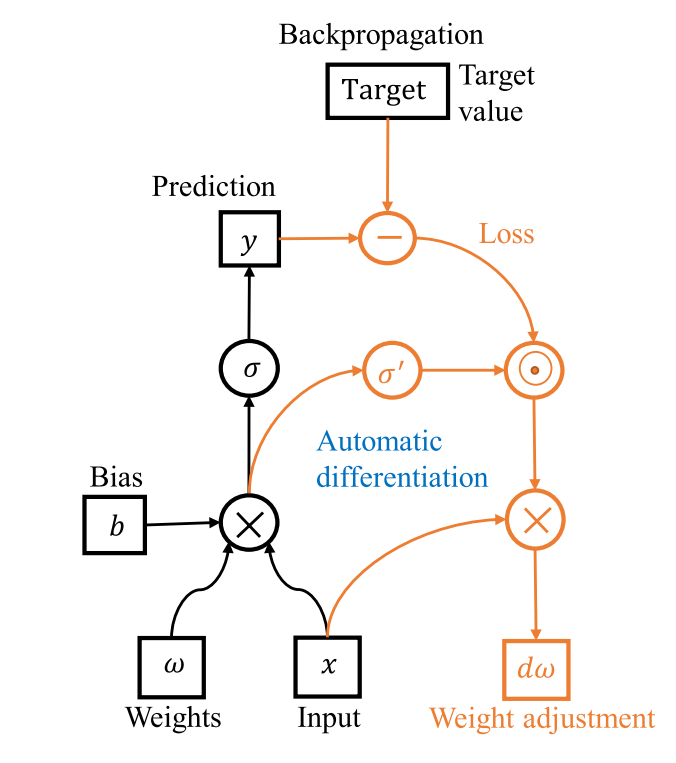
图:前馈神经网络的“计算图”
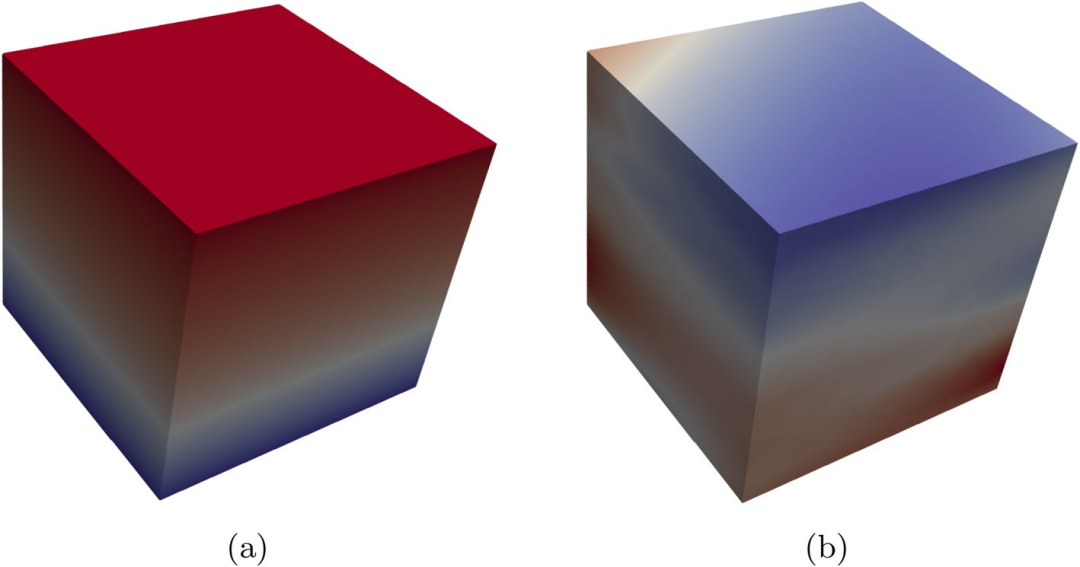
图:功能梯度单位立方体三角材料变化的预测温度和预测函数
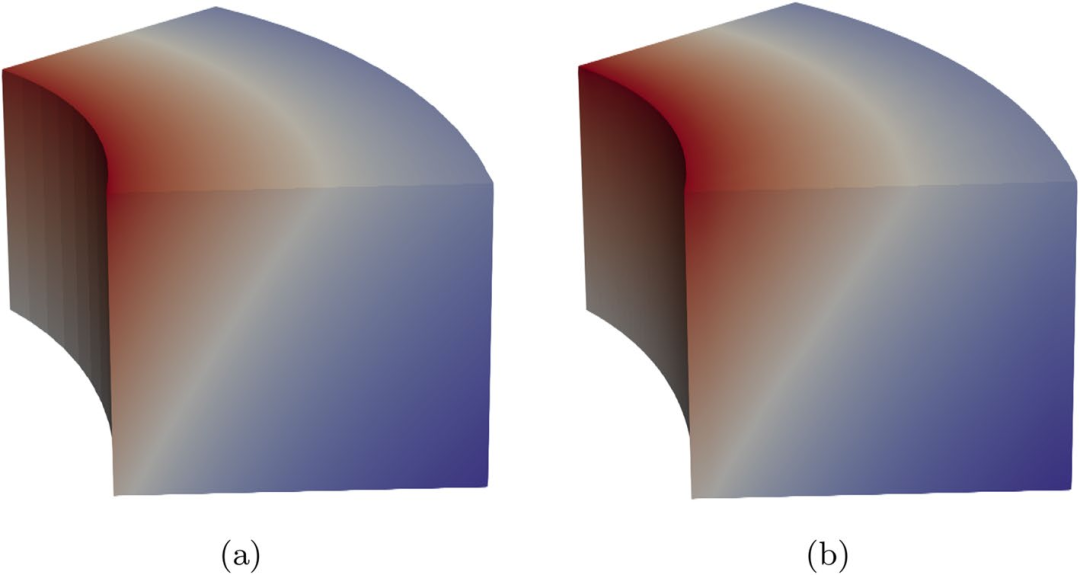
图:通过深部配置法获得的不规则形状 FGM 的通量分布
文五:

基于神经网络结构搜索和传递学习的非均质多孔介质随机深部配置方法
摘要:
针对非均质多孔介质,提出了一种基于神经结构搜索和迁移学习的随机深度配置方法。我们首先进行灵敏度分析来确定网络的关键超参数,以减少搜索空间,然后采用超参数优化来最终获得参数值。所提出的基于NAS的DCM还节省了最有利架构的权重和偏差,然后将其用于fne调整过程。我们还采用迁移学习技术来大幅降低计算成本。然后将所提出的DCM应用于非均质多孔材料的随机分析。因此,建立了一个三维随机fow模型,为高度非均质含水层中地下水fow的模拟提供了一个基准。使用制造解决方案的方法在不同维度上验证了所提出的基于NAS的DCM的性能。我们证明,它在精度和计算成本方面都显著优于fnite-Difference方法。

图:(a)指数相关和 (b) 高斯相关的三维导水率

图:NAS方法和搜索空间的抽象说明

图:NAS的总体方法体系
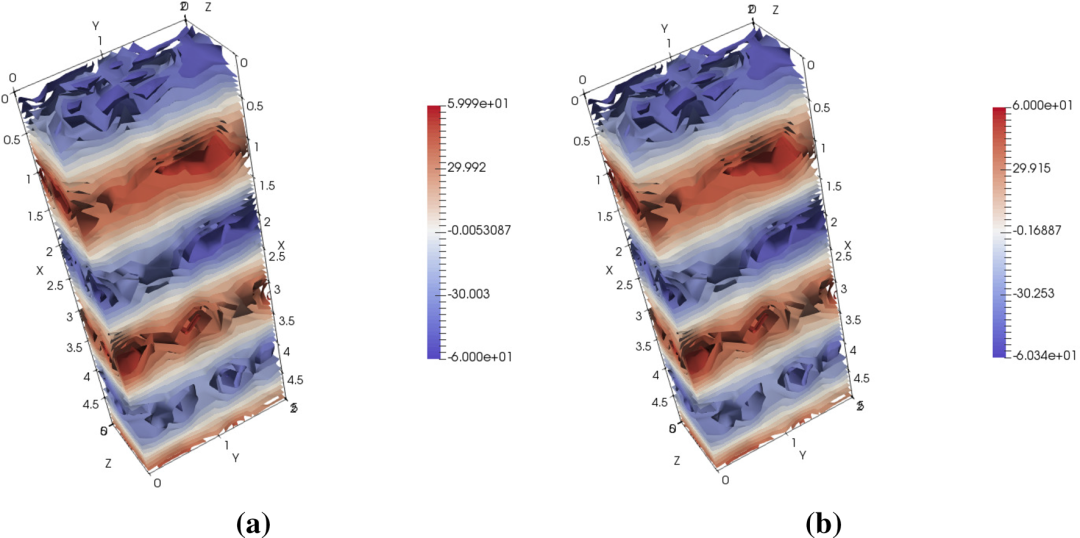
图:三维速度等值面图




