FDEM最新研究进展
文一:

用有限元-离散元组合法模拟砾岩油藏水力裂缝发育
摘要:
众所周知,水力压裂是通过形成水力裂缝来提高裂缝性储层渗透率的最有效的增产措施。HF流体注入的效率在很大程度上取决于预先存在的不连续性或不均匀性的来源。HF操作设计中需要考虑这些特征。在这些特征中,尽管存在于深部岩石中,但基质中含有块体的砾岩储层在很大程度上被忽视了。本研究侧重于HF在此类场地中的发展,并通过使用组合有限元-离散元方法(FDEM)模拟其水力力学行为,该方法完全能够模拟HF在非均质岩石中的传播。首先,根据现有的分析解决方案和实验流体注入验证FDEM的能力,然后将其用于HF开发建模。在砾岩模型中,模拟了三个强度从低到高的块体,以评估块体强度对HF发育模式的影响。研究了各种控制参数,包括原位应力、流速、流体运动粘度、定向HF(DHF)、块体与基体之间的界面性质及其对HF路径的影响。结果显示了矩阵中的块对HF模式的显著影响。HF与不同形状和尺寸的块体的相互作用是复杂的,根据对结果的密切观察,确定了块体的六种相互作用类型。还发现,为了在这样的地层中成功地注入HF,用低粘性流体进行低流速可能是一个好的策略。此外,研究表明,砌块的强度显著影响破坏类型(拉伸或剪切)和破坏压力。
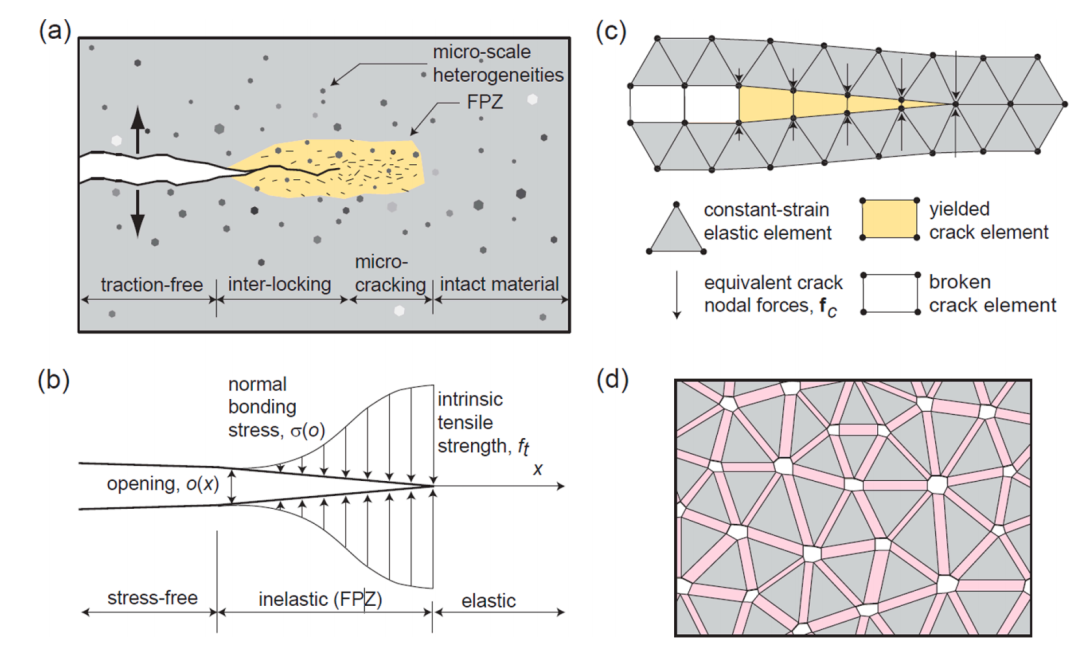
图:(a) 脆性岩土材料中的断裂过程带(FPZ)示意图(在[36]之后);(b) 理论FPZ模型(在[29]之后);(c) FDEM中理论FPZ模型的数值表示(在[44]之后);以及(d)位于所有相邻三角形有限元边缘的4节点裂纹单元的放大视图(在[44]之后)。
图:HF 与块体之间的相互作用类型: (a)阻止,(b)交叉,(c)界面偏转,(d)交叉 + 分支,(e)界面偏转 + 交叉,(f)矩阵分支
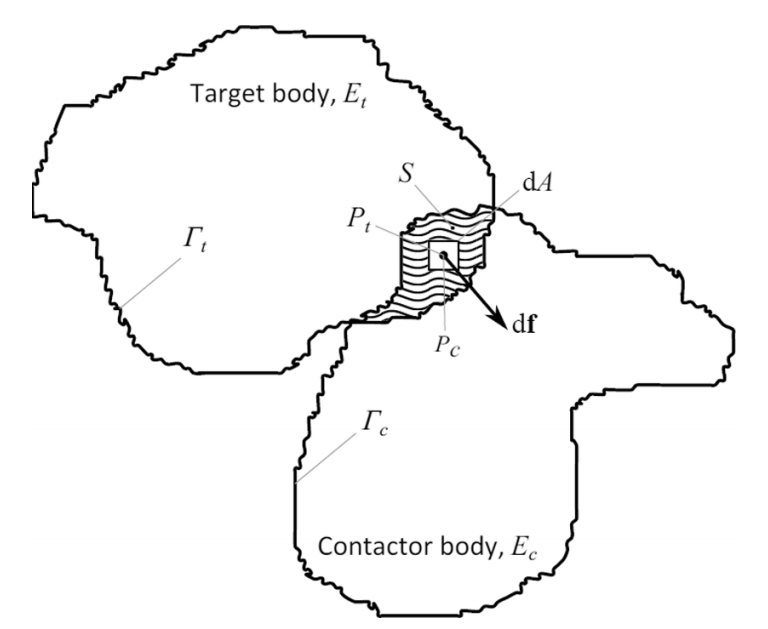
图:由于两个离散物体的无限小的穿透而产生的无限小的斥力的说明

图:在流量和流体运动粘度分别为1kg/s 和1mm2/s 的情况下,包含(a)块1,(b)块2和(c)块3的模型中 HF 的传播路径。
文二:

弹性毛细管现象的有限-离散元组合模型
摘要:
弹性毛细管现象广泛存在于生物和微机电系统中,涉及弹性体的有限变形和液滴/膜的弹性毛细管效应。为了定量分析表面张力的影响,准确预测弹性体的变形,我们建立了超弹性材料的有限应变模型,然后采用组合有限元-离散元法(FDEM)通过显式动力学求解。基于我们的模型,我们研究了弹性体中小空腔的膨胀,并检验了空腔半径和压力之间的关系。此外,我们还研究了浸入液体中并受到表面张力作用的弹性杆的变形。结果表明,当忽略弹性毛细管效应时,随着表面张力的增加,杆的边缘会变得不切实际的粗糙,而表面实际上是光滑的。此外,我们探索了弹性毛细管效应对平面和曲面膜-基底系统中高级多周期褶皱图案的影响,表明可以通过增加表面张力来平滑粗糙的波状表面。我们的研究结果不仅为各种弹性毛细管现象提供了基本的见解,而且为定量指导由表面张力驱动的柔性智能设备的合理设计提供了一个平台。
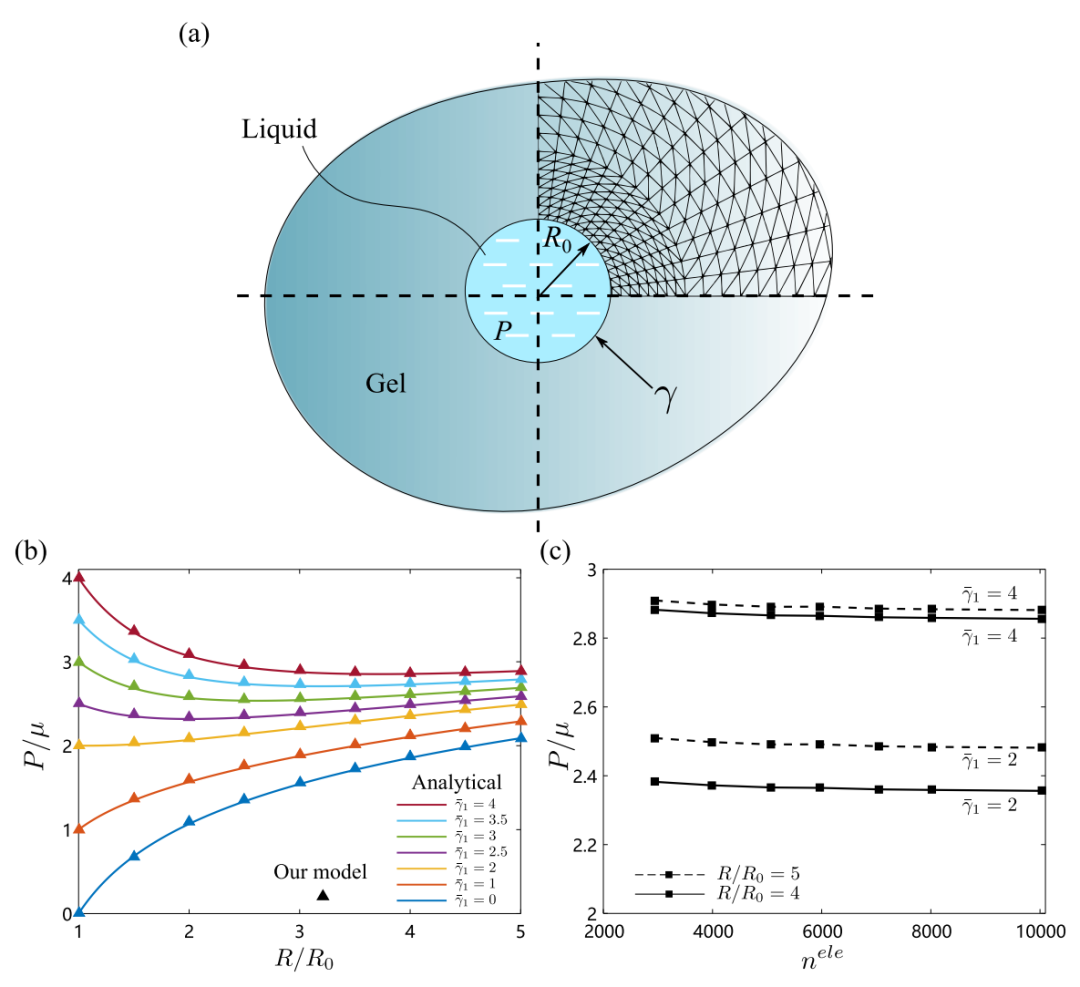
图:弹性体中空腔的计算结果。(a) 无限大弹性体的初始未变形横截面的配置。(b) 无量纲压力的变化𝑃 ∕𝜇 作为无量纲半径的函数𝑅∕𝑅0.(c)具有精细网格的模型的收敛性:无量纲压力𝑃 ∕𝜇 作为元素数量的函数。
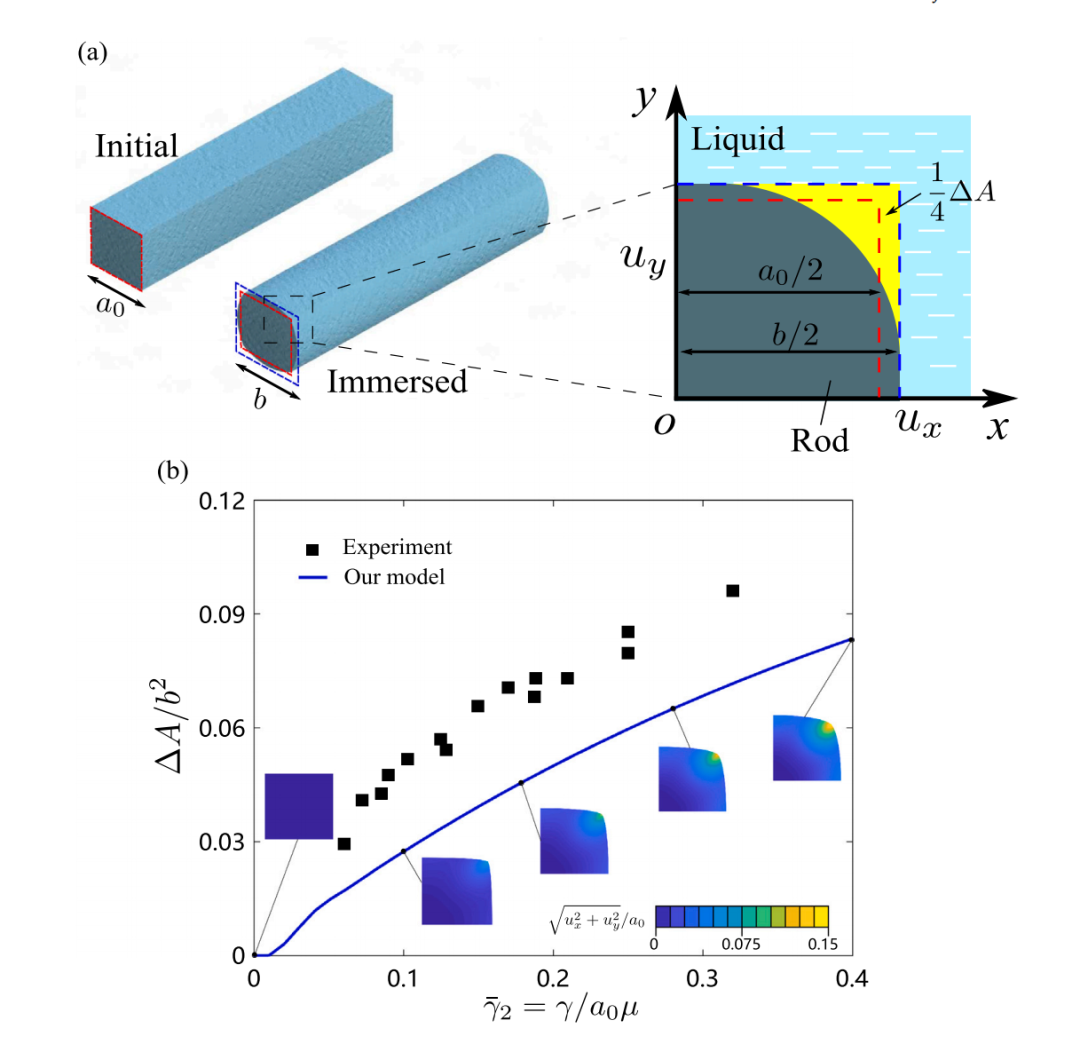
图:浸入式弹性杆的平滑处理。(a) 具有方形横截面的弹性杆在浸入液体中时变得光滑。红点线表示横截面轮廓(带边长𝑎0),而蓝点线表示理想的展开正方形(具有边长𝑏). 黄色 区域𝛥𝐴 是理想面积之间的差异𝑏2和实际变形横截面。(b) 实验(黑色方点)[5]和我们的模型预测(蓝色实线)之间的比较。插图展示了杆1/4横截面的变形
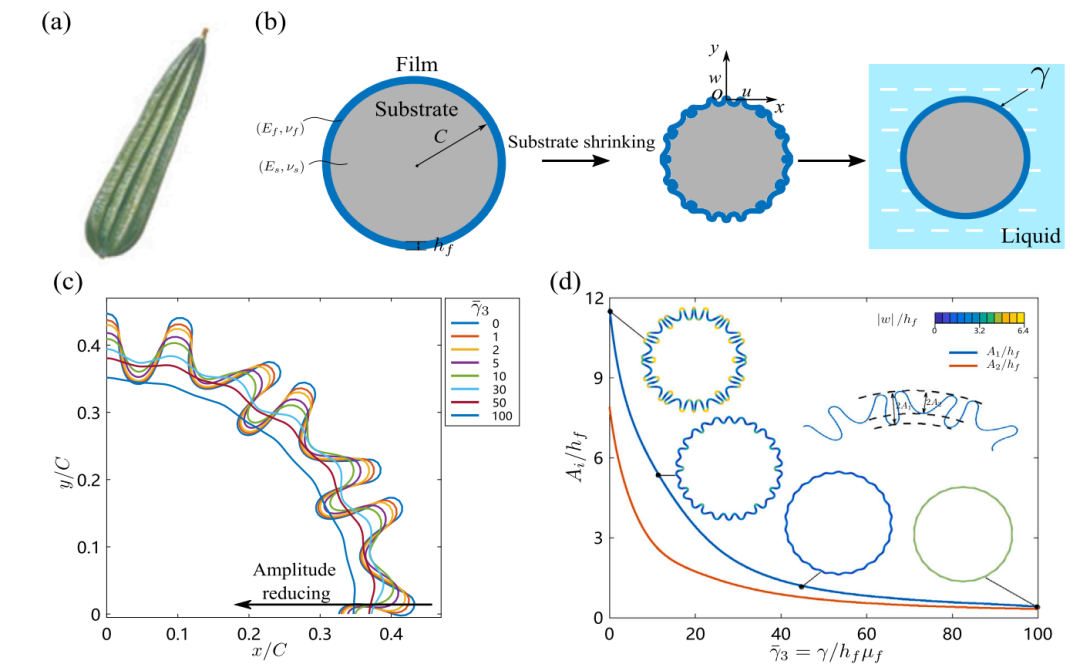
图:弹性毛细管对收缩核壳系统的影响。(a) 有脊的葫芦[46]。(b) 浸没在液体中的收缩芯壳系统示意图。(c) 薄膜在不同表面张力下的倍周期形态演变。(d) 振幅𝐴𝑖(𝑖 = 1,2)作为弹性毛细管数的函数𝛾3.。插图显示了胶片的偏转。
文三:

有限元-离散元耦合法(FEM/DEM)模拟超高速撞击
摘要:
轨道碎片的超高速撞击(HVI)对当前和未来的近地轨道任务构成了越来越大的威胁,使航天器屏蔽对未来的太空探索工作至关重要。碎片防护罩是一种牺牲板,它将撞击器粉碎成粒子云,将撞击器的动量分布在大面积上,从而防止其穿透航天器。在这项研究中,在LS-DYNA中使用耦合有限元离散元法(FEM/DEM)对碎片防护罩上的HVI进行建模,其中失效的固体单元被转换为离散颗粒。将结果与文献中测试配置系统变化的实验数据进行比较,以进行验证。模拟了直径小于1cm、冲击速度为6.7km/s的射弹的正常撞击,以研究薄板穿孔后碎片云的形成。铝合金AA6061-T6的材料数据用于靶材和射弹。FEM/DEM方法能够预测作为屏蔽厚度函数的碎片云的形状,并进行了参数研究以研究关键模型参数的敏感性。然后,确定了双壁惠普尔盾和面积质量相等的相应单片结构在1至14km/s速度范围内的弹道极限曲线。同样,FEM/DEM方法的预测与文献中的结果接近。

图:目标厚度研究的射线照片𝑡∕𝐷 = 0.102,撞击速度为6.72 km/s,显示为三个时间点的撞击合成图像
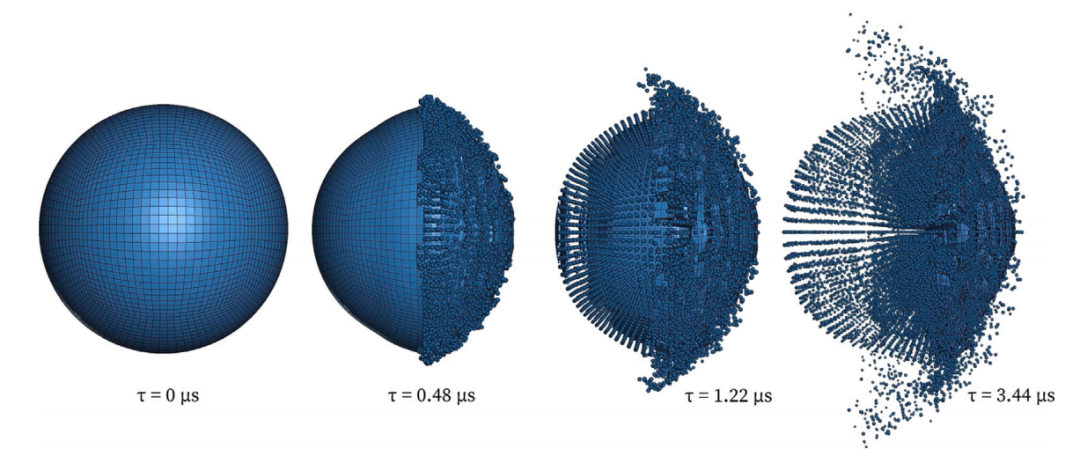
图:碰撞后从固体元素到粒子的转换,显示为𝑡∕𝐷 = 冲击速度为6.7km/s时为0.084

图:目标厚度研究的数值结果𝜏与Piekutowski的实验结果相比,撞击后3=20μs,具有线性和非线性EOS
文四:

孔隙形态对多孔岩石压裂特性的影响
摘要:
提出了一种生成具有可控形状特征的随机孔隙几何结构的系统方法,用于更真实的多孔岩石材料数值建模。通过将零厚度粘性单元与有限实体单元相结合,建立了数值模型(有限离散模型),以跟踪多孔岩石的渐进破裂和破坏行为。对使用3D打印技术生成的合成试样进行了一系列巴西劈裂试验,以验证所提出的数值模型。通过对比压裂模式和荷载-位移曲线,表明所提出的混合数值方法在捕捉多孔岩石的力学响应方面具有良好的性能。此外,还讨论了孔隙纵横比和方位对多孔岩石力学和破裂响应的影响。通过计算内聚单元的总损伤率(Pt)和剪切损伤率(Ps),混合方法为揭示不同孔隙形态特征引起的强度变化机制提供了微观见解。建模结果表明,多孔岩石更好的力学性能对应于更高的Pt和Ps值。建模结果与文献数据之间的比较也验证了所提出的混合方法的有效性和准确性。
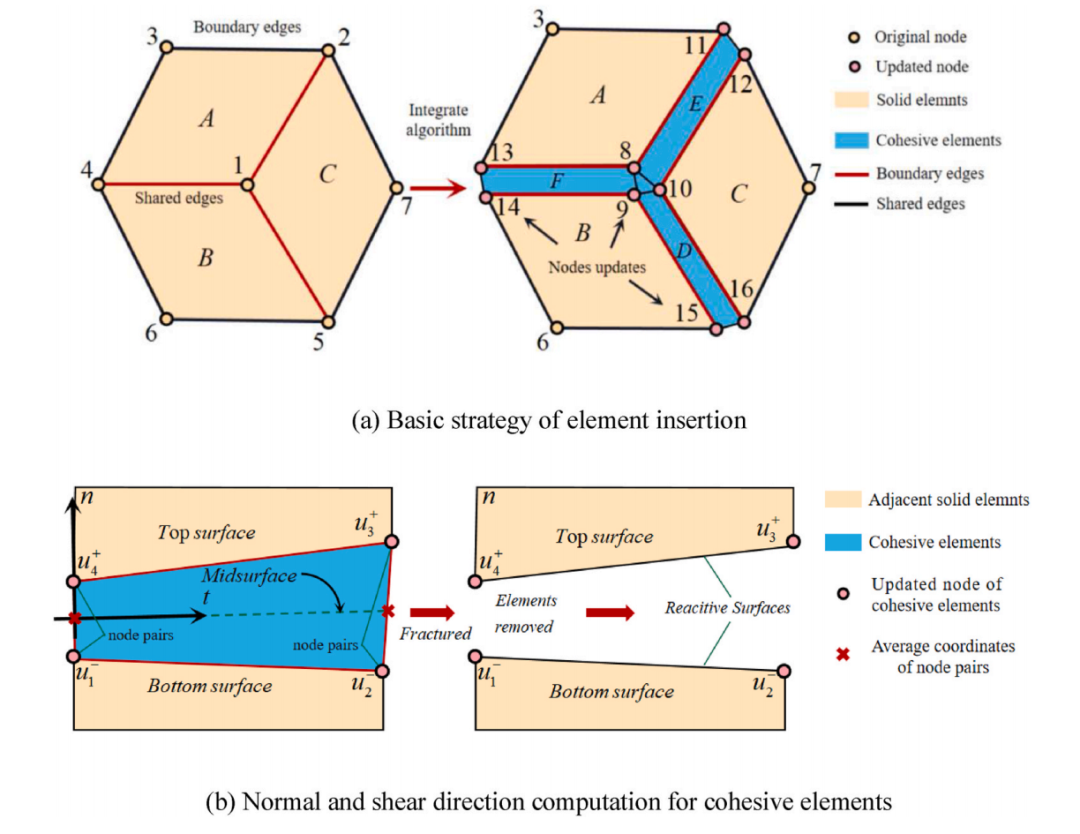
图:粘性单元的插入方法和本构模型。

图:多孔试样的制备。

图:具有不同纵横比的试样的失效模式。

图:孔隙形态数据库的建立。
文五:

用有限元-离散元组合法模拟岩石边坡的整个渐进破坏过程
摘要:
本文提出了一种新的方法(Y型边坡)来模拟从初始、迁移到沉积的整个边坡破坏过程。该算法在组合有限元-离散元方法代码中实现。采用吸收边界条件来提高初始应力状态平衡的计算效率。采用考虑拉伸和剪切破坏模式的强度折减方法来评估边坡稳定性,其中安全系数和临界破坏面是自动获得的。由于块体的摩擦和碰撞,结合了能量耗散机制,以准确模拟故障后阶段的块体运动学。通过数值试验验证了Y型边坡的准确性和稳健性,并给出了均质节理岩石边坡的破坏机理和破坏过程。结果表明,Y型边坡不仅可以评估边坡的稳定状态(如安全系数和临界破坏面),还可以模拟整个破坏过程(如边坡变形、破坏面演化、块体迁移和沉积)。此外,还强调了现有不连续性对边坡稳定性和破坏机制的关键作用。这项工作提出了一个很有前途的工具,通过预测岩石边坡的整个破坏过程来了解破坏机制和评估潜在风险。

图:两个接触块之间的接触力计算示意图。红色体和蓝色体分别表示接触体和目标体。
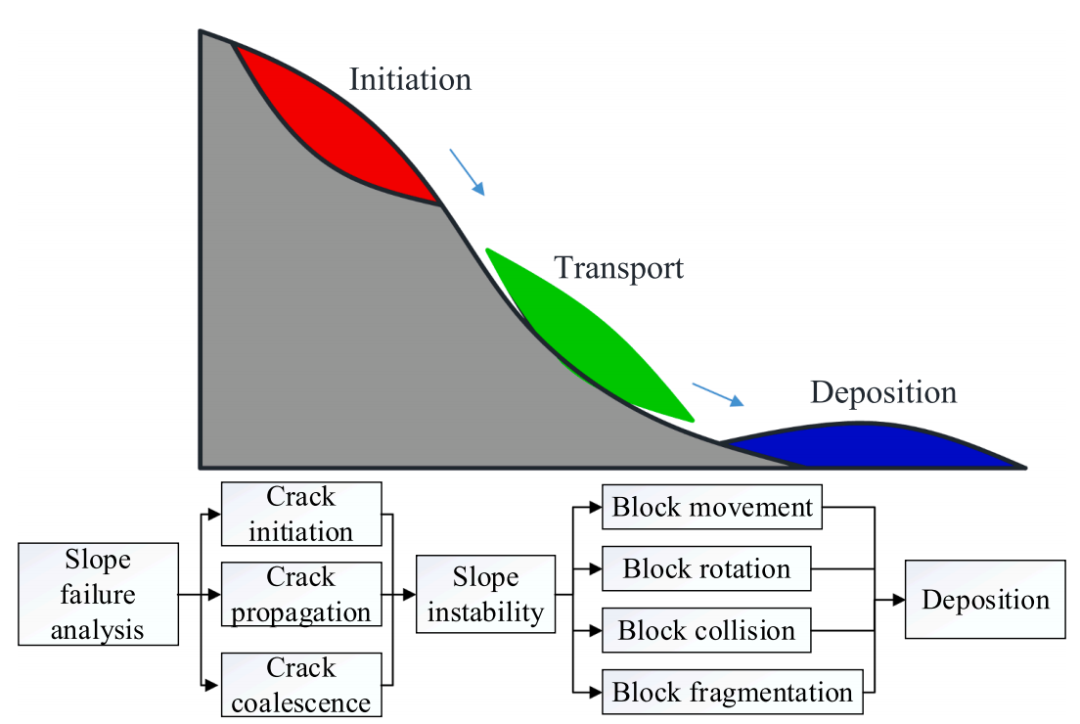
图:对整个边坡破坏过程的分析。
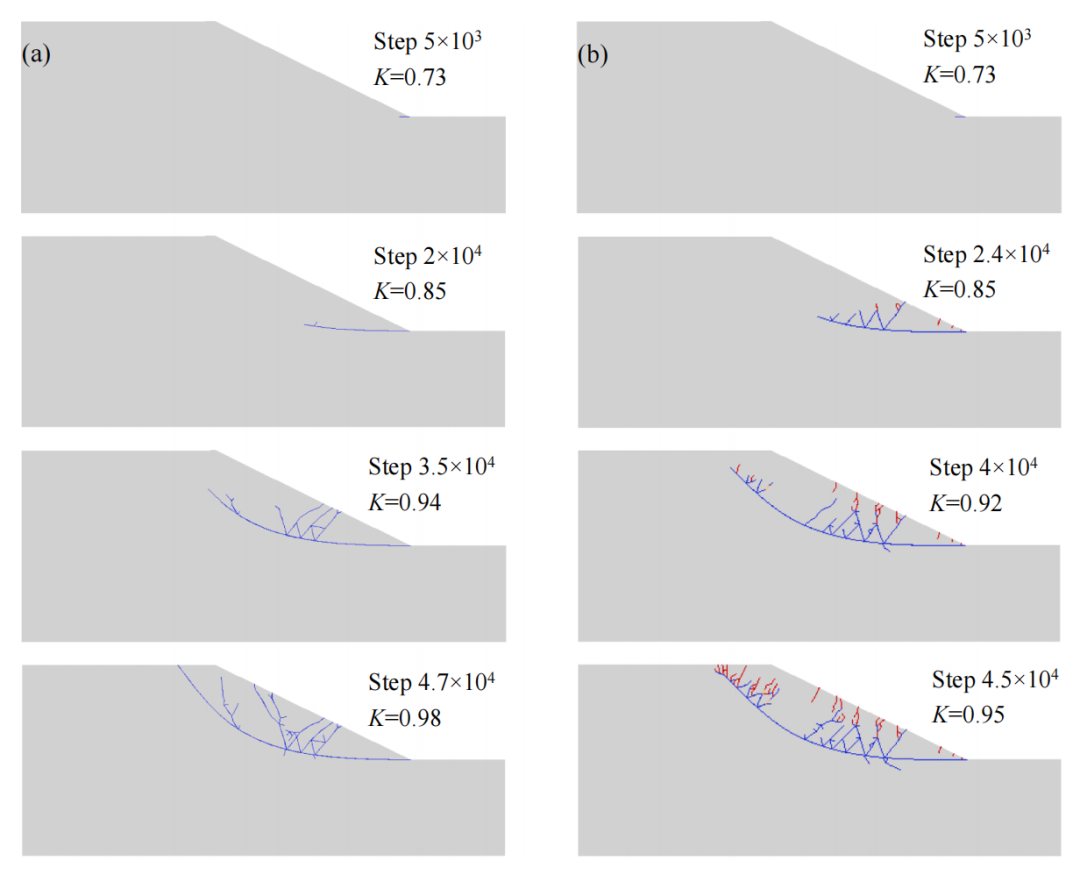
图:岩石边坡的渐进破坏具有(a)纯剪切和(b)拉伸剪切破坏模式。剪切失效为蓝色,拉伸失效为红色,混合失效为橙色。

图:(a) 中国小湾水电站水库边坡梯级路径破坏模式的现场观测和(b)数值模拟




