计算力学开源代码大放送
文一:

基于开源代码的贝叶斯反演解决计算力学中的各种一维模型问题
摘要:
计算力学中许多问题的复杂性要求有可靠的编程代码和精确的模拟系统。通常,模拟响应强烈依赖于材料和模型参数,其中区分了后向模型和前向模型。为材料/模型参数提供可靠信息,使我们能够校准正向模型(例如,偏微分方程系统)。马尔可夫链蒙特卡罗方法是估计参数后验密度的有效计算技术。在本研究中,我们将贝叶斯反演应用于几个力学问题,并研究其适用性以提高模型的准确性。提出了耦合多场(和多物理)系统中的七个不同边值问题。为了提供全面的研究,同时考虑了与速率相关和与速率无关的方程。此外,开源代码(https://doi.org/10.5281/zenodo.6451942),构成了用于例如多场耦合问题的未来发展的方便平台。开发的软件包是用MATLAB编写的,提供了有关机械模型问题和反向贝叶斯反演设置的有用信息。
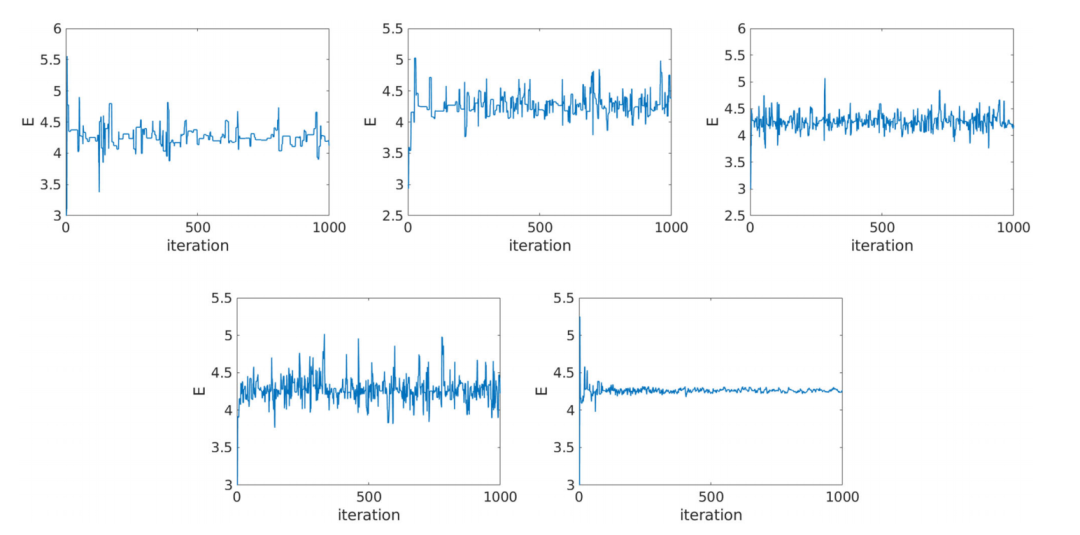
图:示例1。通过不同的贝叶斯技术获得E的MCMC链。从左到右:MH、AM和DR(第一行),DRAM和EnKF(第二行)
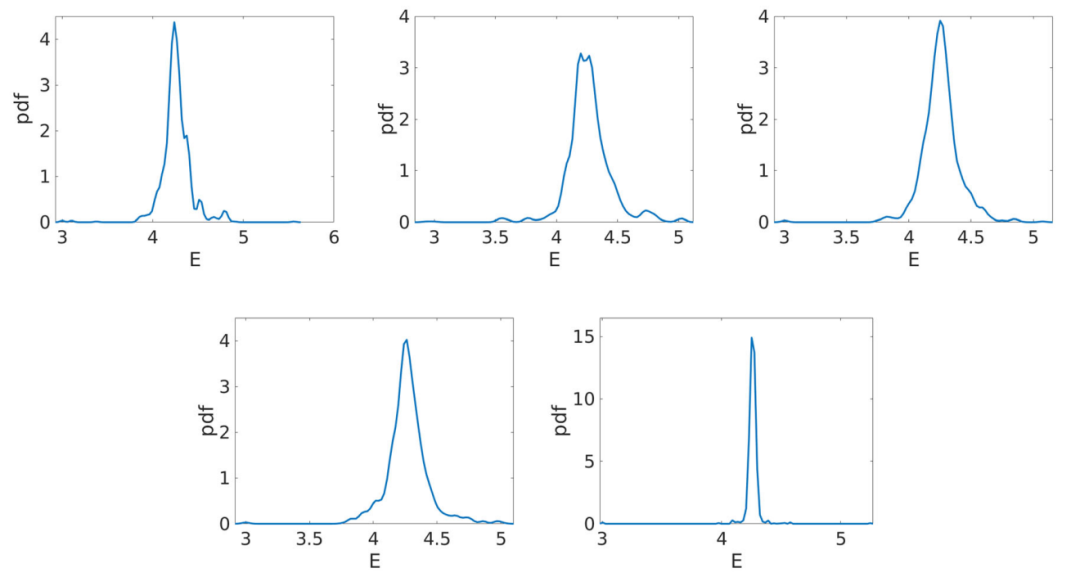
图:示例1。通过不同的贝叶斯技术获得的E的后验分布。从左到右:MH、AM和DR(第一行),DRAM和EnKF(第二行)

图:例子4。用 EnKF 方法估计不同参数的后验密度。真实值用绿色虚线表示。
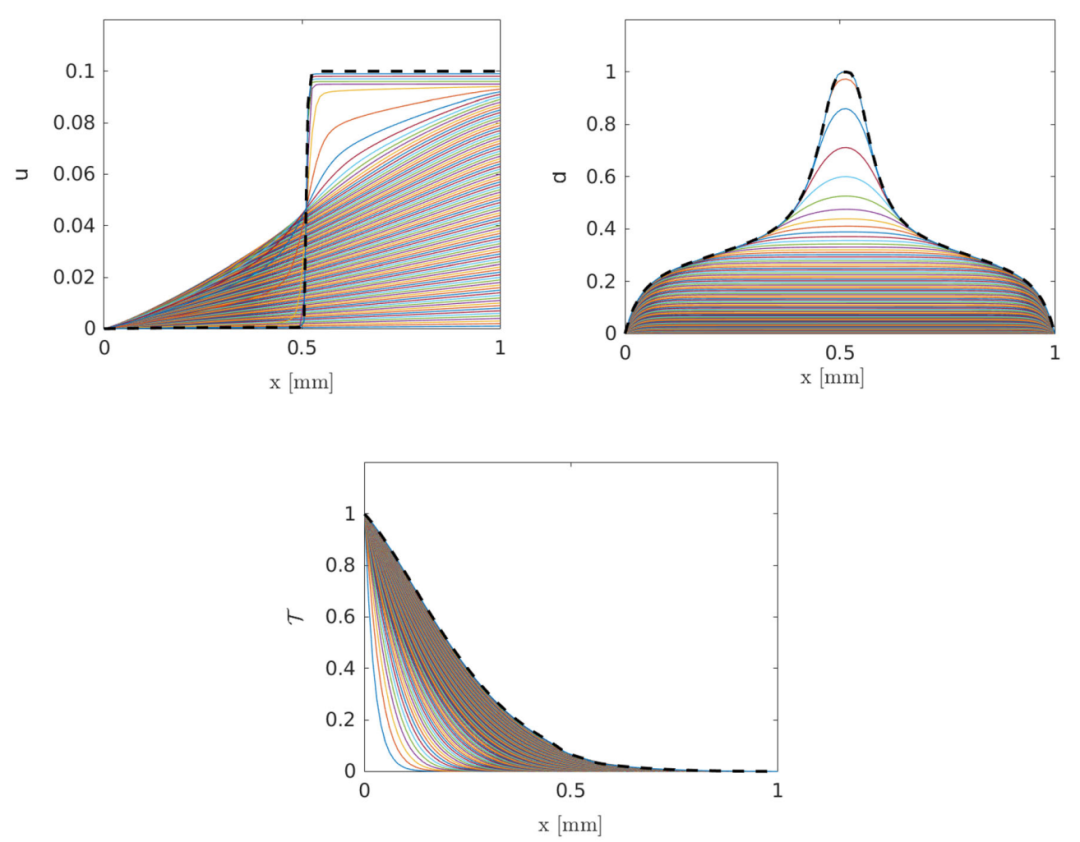
图:例子6。位移(左上)、相场(右上)和温度(下)在不同时间步长中的演变。用于贝叶斯反演的最后一步显示为黑色虚线
文二:

计算力学中的Julia语言:一个新的竞争者
摘要:
数值方法是计算力学中最流行的工具,已被用于解决各种实际工程问题。然而,用于实现数值方法的最常见的编程语言并不能有效地平衡生产力和效率的要求。为了解决数值计算中计算密集度最高的领域,通过高级语言提高抽象性和生产力,麻省理工学院(MIT)于2012年发布了Julia语言。Julia语言是一种开源程序ming语言,语法简单,性能令人满意;这对于科学计算特别有用。本文对Julia语言在计算力学中的应用进行了全面的综述。首先,我们介绍了现有的用Julia语言开发的数值计算软件包及其相关应用。其次,我们分析了Julia语言在计算力学软件包开发中的能力。最后,我们讨论了关于Julia语言的悬而未决的问题,以及在计算力学中使用Julia语言所面临的挑战。

图:常用的基于网格的方法和无网格方法
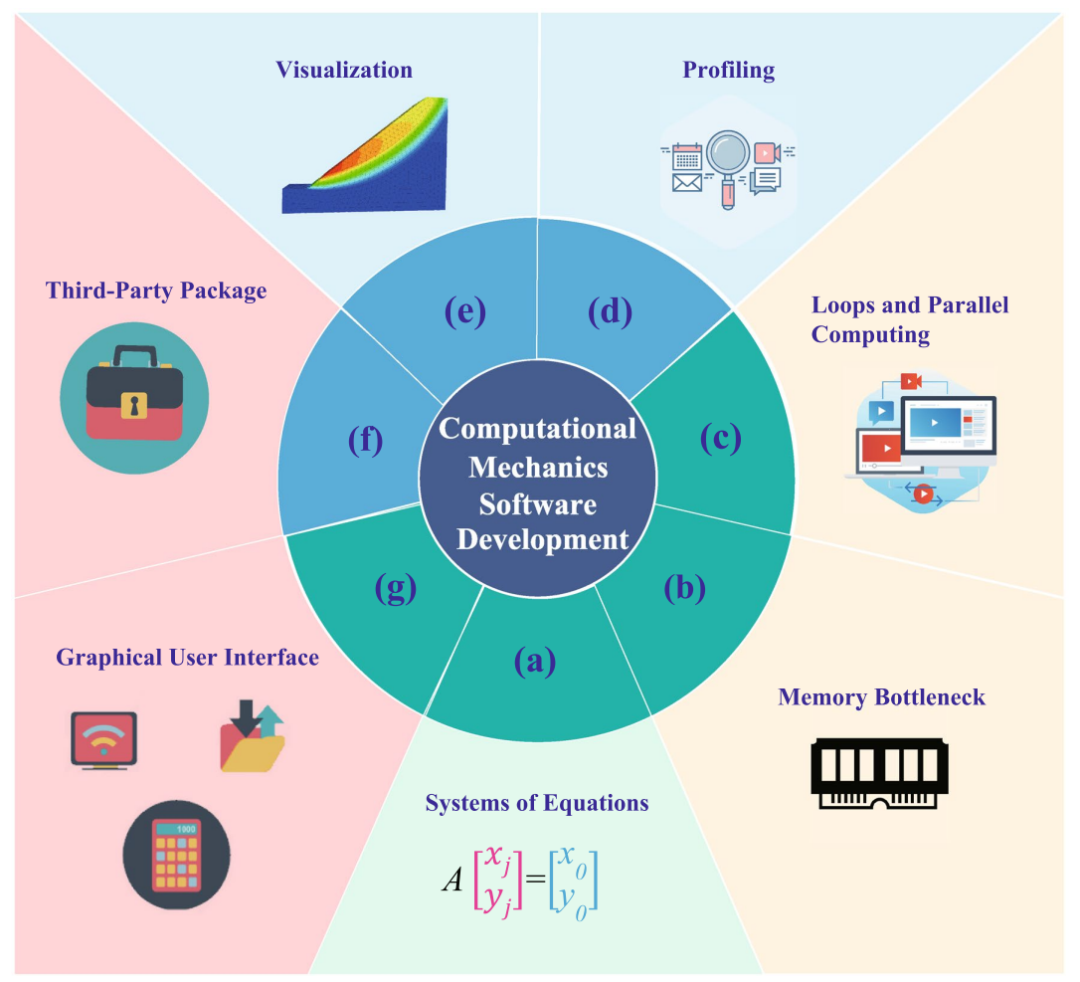
图:计算力学软件开发中的常见问题
文三:

用于材料失效多尺度建模的计算库
摘要:
我们提出了一个名为PERMIX的开源软件框架,用于固体裂缝的多尺度建模和模拟。该框架是一个面向对象的开源工作,主要使用Fortran 2003标准编写,带有许多其他库(如LAMMPS、ABAQUS、LS-DYNA和GMSH)的Fortran/C++接口。采用扩展有限元方法(XFEM)对连续体层面的断裂进行了建模。使用几种新颖或最先进的方法,该软件处理半并发多尺度方法以及并发多尺度断裂方法,分别将两个连续域或原子域耦合到连续域。我们的开源软件的效率通过几个模拟来展示,包括粘土纳米孔中的3D裂纹建模、半并发FE-FE耦合、3D Arlequin多尺度示例和用于动态裂纹扩展的MD-XFEM耦合。
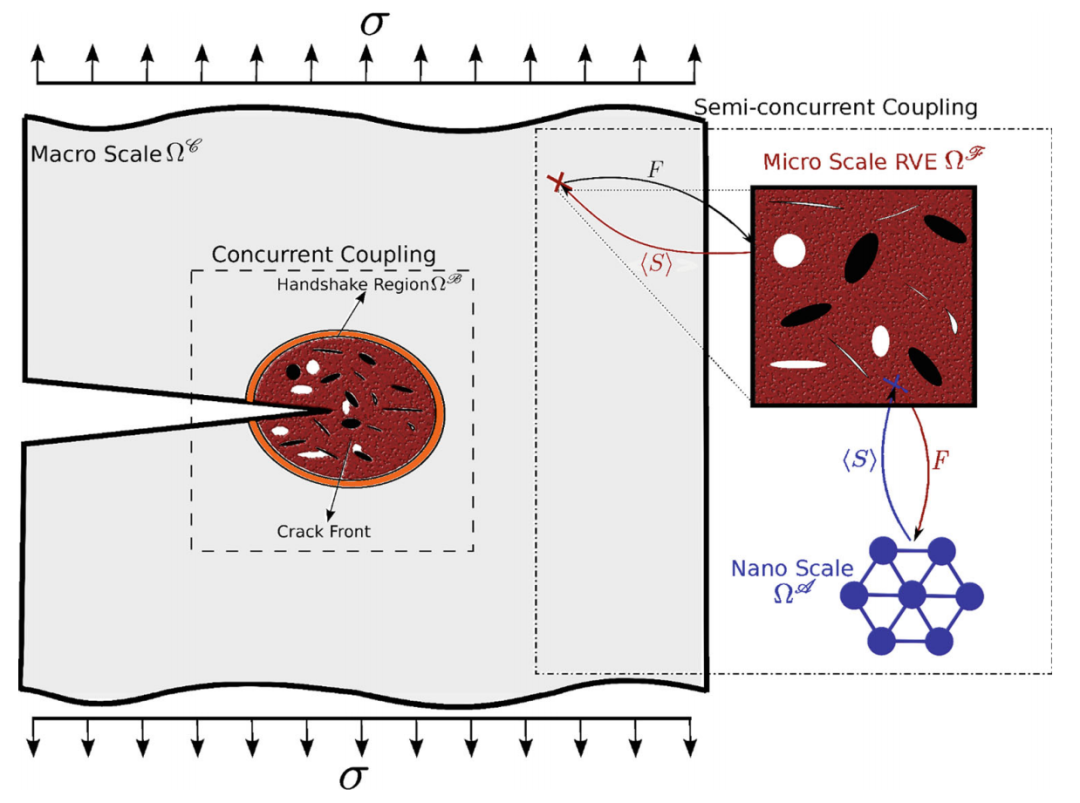
图:并发和半并发多尺度方法示意图
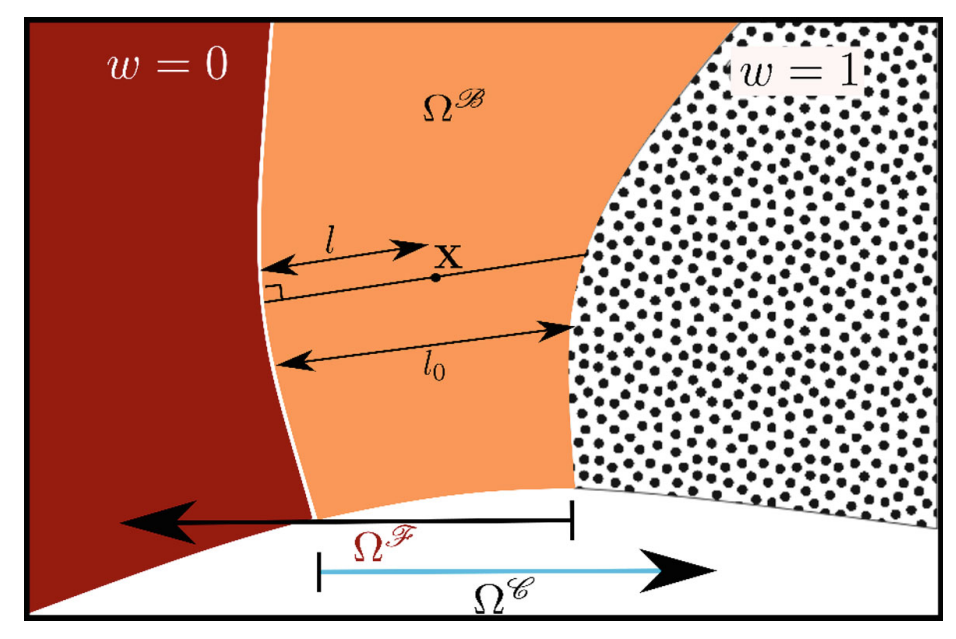
图:二维握手域中的加权函数
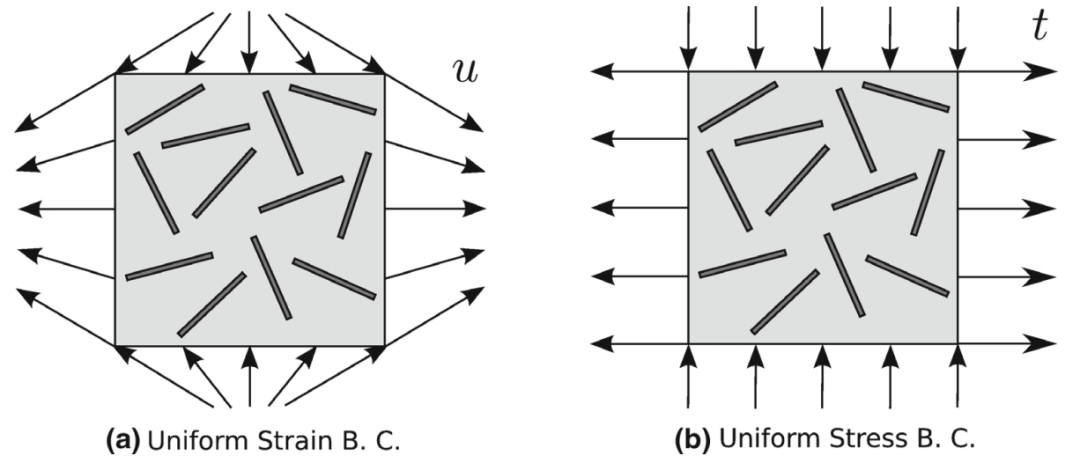
图:不同的边界条件方法。a均匀应变和b均匀应力边界条件
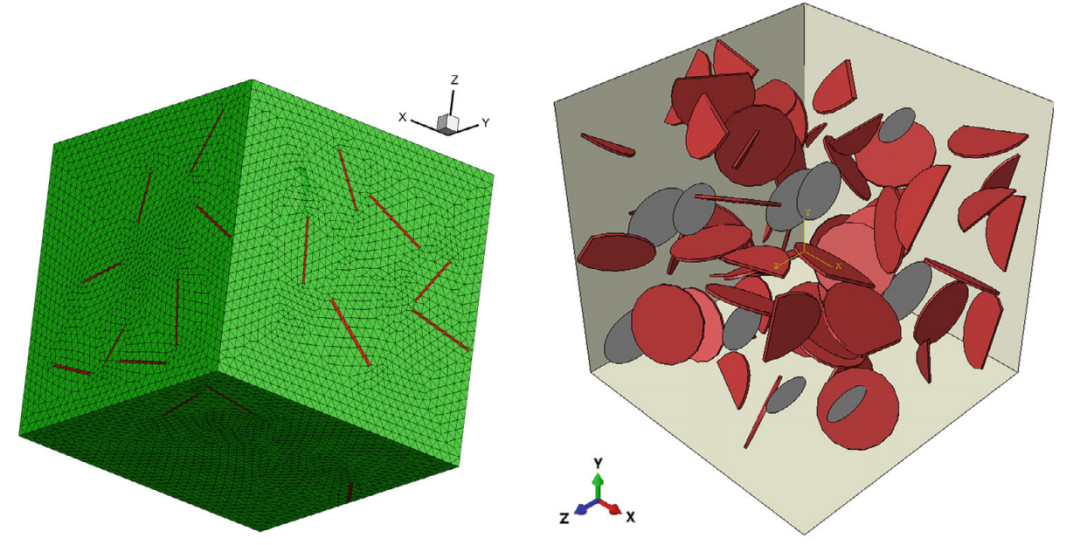
图:三维 RVE 包括随机定向和分布的粘土颗粒(红色硬币形状的物体)和裂纹(灰色椭球体)。
文四:

通过机器学习求解计算力学中偏微分方程的能量方法:概念、实现和应用
摘要:
偏微分方程(PDE)是对科学和工程中的不同现象进行数学建模的基础。解决它们是迈向精确了解自然和工程系统行为的关键一步。通常,为了在可接受的程度上求解表示真实系统的偏微分方程,分析方法通常是不够的。必须采用离散化方法。对于工程问题,最著名的选择可能是有限元法。然而,也有强大的替代方法,如无网格方法和等几何分析(IGA)。其基本思想是通过专门构建的具有一些理想性质的函数来近似PDE的解。在这篇文章中,我们探索了深度神经网络(DNN)作为近似的一种选择。他们在视觉识别等领域取得了令人印象深刻的成果。DNN在这里被视为函数逼近机。定义它们的结构有很大的灵活性,架构和算法的重要进步使DNN成为一种非常有趣的替代方案,可以近似PDE的解决方案。我们专注于对计算力学感兴趣的应用。大多数研究这种可能性的贡献都采用了搭配策略。在这项工作中,我们专注于机械问题,并分析PDE的能量格式。机械系统的能量似乎是机器学习方法处理机械问题的自然损失函数。为了证明这些概念,我们处理了几个问题,并探索了该方法在工程中的应用能力。
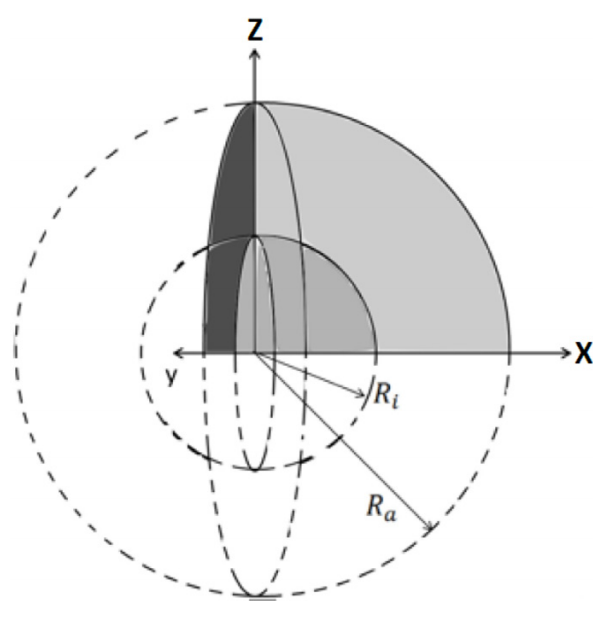
图:内部压力下的空心球体。几何设置和边界条件。
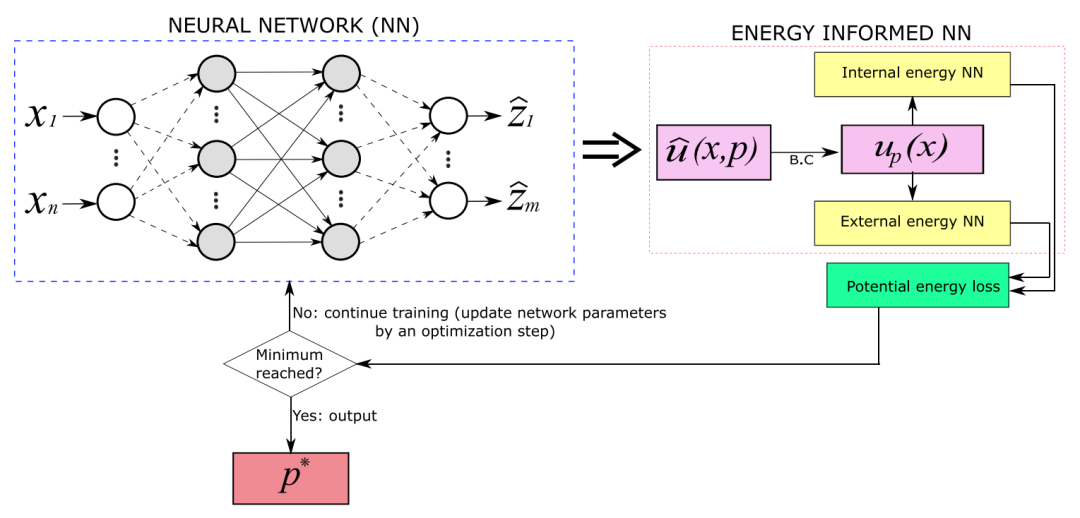
图:深能量法的全过程。
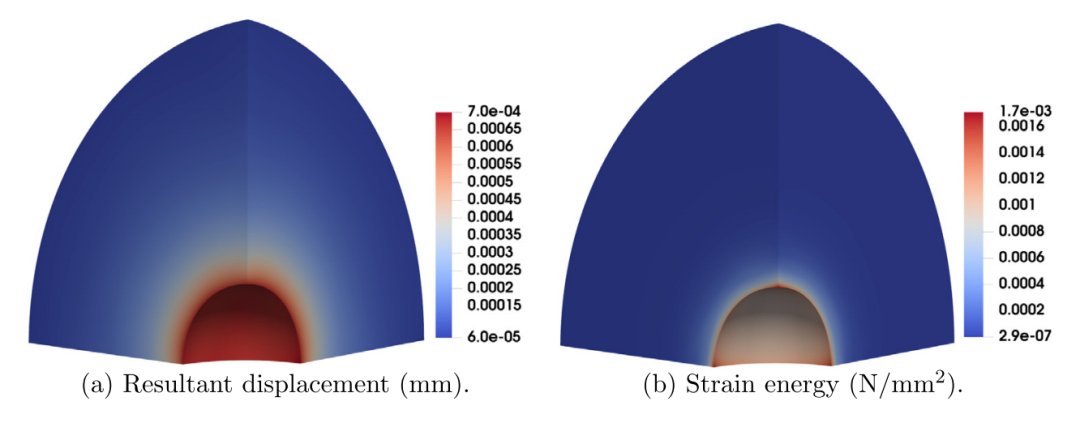
图:承受内压的空心球的预测解。
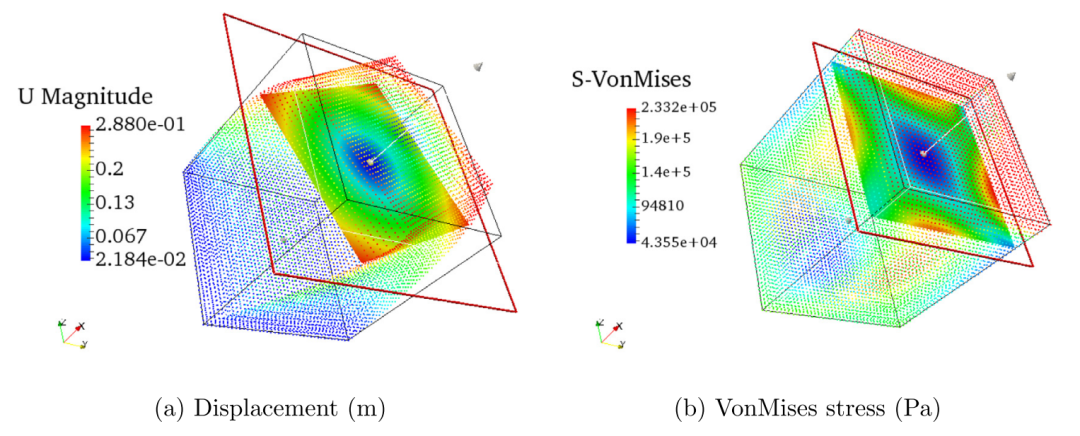
图:扭曲 Neo-Hookean 长方体 DEM 中 CDEF 平面的位移大小和 VonMises 应力。
文五:

基于 Fourier 级数的不规则颗粒计算力学的离散元方法
摘要:
许多天然和工程颗粒材料主要由不规则形状的非球形颗粒组成。本文针对不规则形状粒子的计算力学,提出了一种新的基于傅立叶级数的离散元方法。在FS-DEM中,引入了基于傅立叶级数的粒子几何描述和坐标表示,其中粒子形状由FS系数隐式确定,FS系数保持不变,与粒子位置或运动学无关。然后,使用基于FS的粒子表示,开发了接触检测和解析算法来识别接触并解析接触几何特征。FS-DEM方法是利用传统的接触行为、运动定律和运动积分来完成的。通过三个算例评估了FS-DEM框架的精度和计算效率,并与基于重叠离散元聚类的DEM方法进行了比较。结果证明了FS-DEM方法的鲁棒性和优越性,以及它在不规则形状粒子系统的有效计算建模中的潜力。

图:不规则粒子的局部坐标系和全局坐标系的图示。
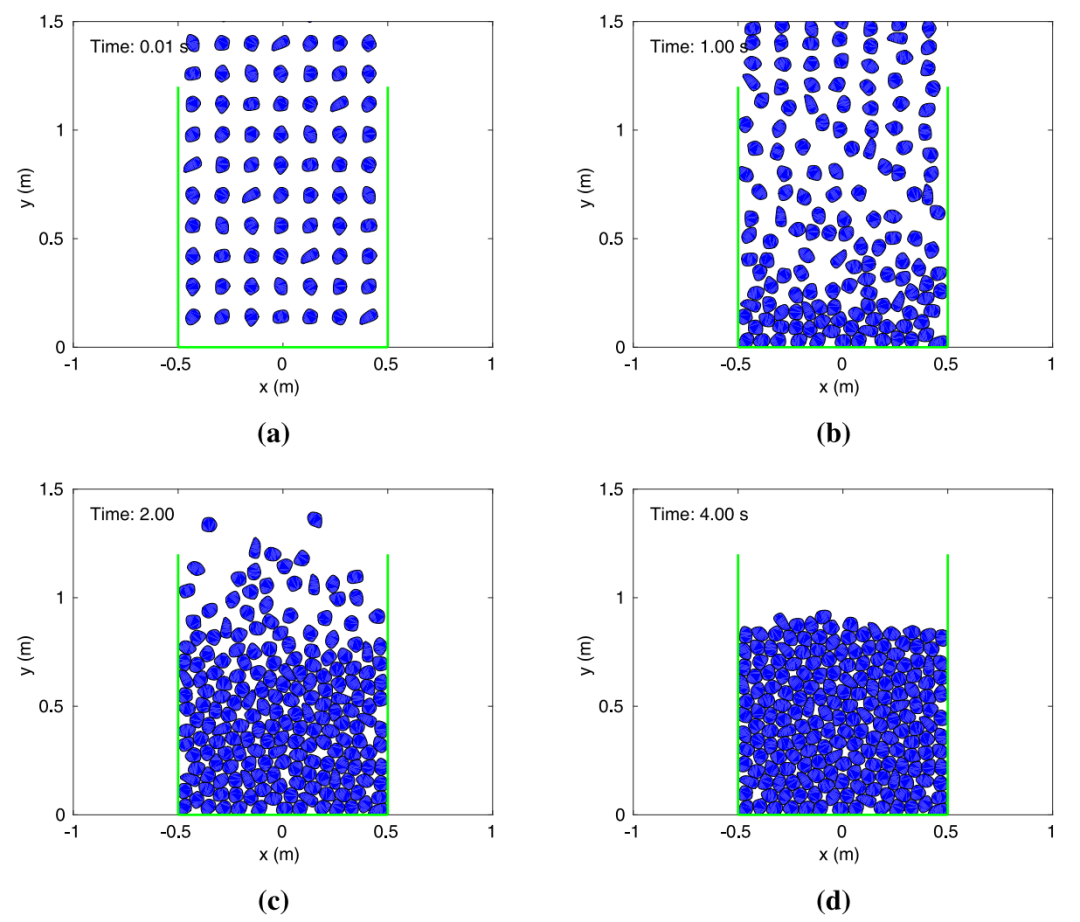
图:在 t = 0.01,1,2和4s 时所拍摄的快照显示了不规则颗粒的沉积过程。

图:压缩过程不同阶段的颗粒堆积(顶部)和接触织物(底部):ε=0%(左)、ε=6%(中)和ε=12%(右)。粉红色的线表示粒子的方向,黑色的粗线表示接触力链。
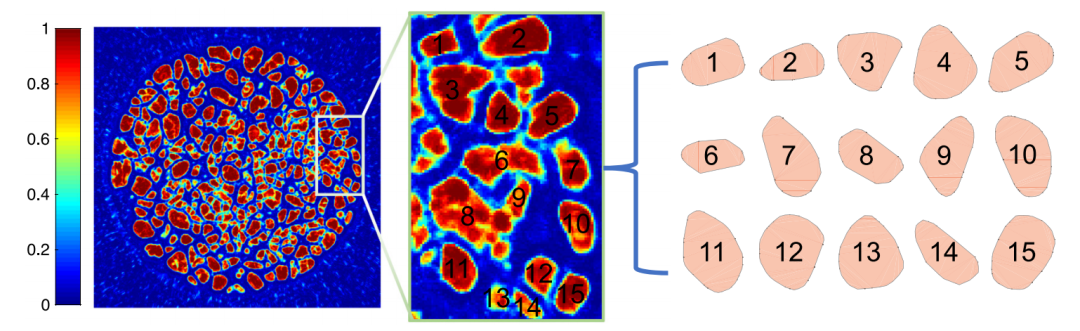
图:从莫哈韦火星模拟的 X 射线 CT 图像重建的形状模板。




