物质点法(material point method)的最新研究进展
文一:

物质点法模拟两相多孔岩土材料的流体力学行为: 最新进展
文一:
物质点法(MPM)作为解决涉及大变形的流体力学耦合问题的合适方法,越来越受欢迎。在本文中,我们综述了两相多孔岩土材料水力力学行为的MPM模拟的最新进展。综述了MPM的最新进展和发展,以及它们的扩展,以捕捉涉及大变形的水-力耦合问题。这一观点的重点是为模拟两相耦合大变形问题提供一个清晰的画面,这将为从业者和研究人员提供一些直接的参考。

图:一类典型问题域的 MPM 离散化。

图:采用两组物质点来描述两个阶段响应的耦合 MPM 实现

图:采用传统有限元方法进行大变形边坡崩塌分析: (a)初始未变形网格; (b)最终变形形态。
文二:

金属三维打印过程中热-流-固耦合问题的多物理物质点法
摘要:
金属增材制造(AM)过程涉及与传热、流体流动和固体力学相关的复杂多物理耦合现象,这给当前的数值方法带来了挑战。在这项研究中,提出了一种多物理物质点方法来解决金属增材制造过程中的热流体-固体耦合问题。在这种方法中,材料域由一个结构化网格和一组粒子离散化,在欧拉和拉格朗日描述下,这些粒子具有热传递、流体流动和热应力演化的相应变体。这些场之间的相互作用自然由相同的结构网格和粒子处理。此外,提出了一种半隐式局部迭代技术来有效求解固液相变换热,引入了一种改进的Chorin投影方法来处理Darcy阻尼,并提出了一个带有子单元占用技术的交错推导方案来求解表面张力和Marangoni力。给出了一组数值例子,包括基准问题和选择性激光熔化AM问题,以验证所提出的方法,其中与文献中可用的分析、数值和实验数据取得了良好的一致性。结果表明,所提出的方法是解决金属增材制造中的热流固耦合问题和其他多物理问题的有力工具。

图:选择性激光熔化过程中考虑的领域

图:(a)传热、(b)流体和(c)固体结构域的细胞和颗粒标记。

图:固液相变问题的验证。

图:选择性激光熔化问题的热流体耦合模拟:(a)温度和粒子状态;(b) 实验与数值结果的比较。
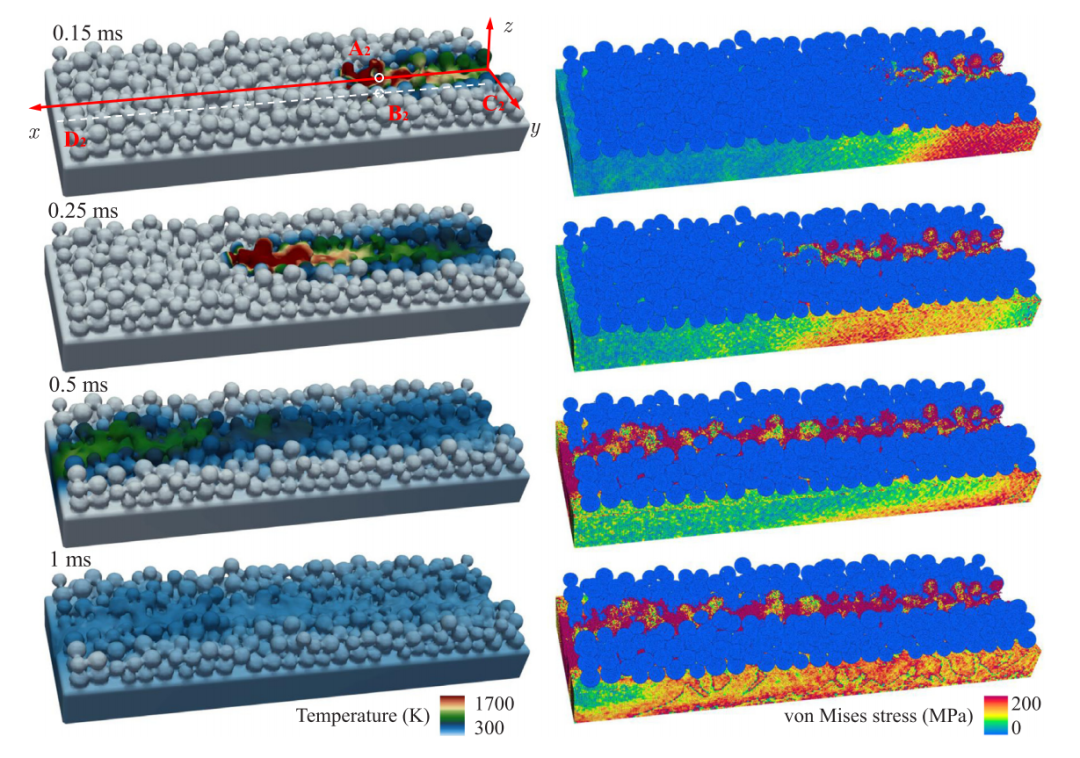
图:50μm 厚粉末床 SLM 问题的表面形貌和不同时间点的 von Mises 应力。
文三:

一种改进的模拟饱和岩土材料大变形问题的半隐式材料点法
摘要:
基于分步法,提出了一种改进的求解岩土工程大变形耦合问题的半隐式MPM公式。本研究的主要目的是选择与渗透率无关的时间步长,并通过应用特殊的分裂程序和稳定技术来减少压力振荡。通过将一维固结问题在小变形和大变形状态下的数值结果与解析解进行比较,验证了所提出的耦合MPM。为了进一步评估该方法的性能,进行了三次数值试验,包括自重滑塌块、二维固结试验和饱和弹塑性边坡的稳定性。数值结果表明,该方法适用于模拟大变形的流体饱和多孔介质。

图:两相多孔介质的图形表示。

图:最终加载阶段的边坡模型轮廓(SRF = 1.5)。

图:不同渗透率边坡的水平位移和塑性应变。
文四:

土强度线性增加不稳定边坡大变形特性的随机材料点法参数分析
摘要:
土壤通常表现出具有非平稳性的空间变异性,这尚未在边坡破坏后分析的背景下进行研究。本研究采用随机材料点法研究了非平稳性对空间可变不排水抗剪强度边坡大变形特性的影响。非平稳性对大变形特征的平均值和标准差有显著影响,忽略非平稳性会导致更高的平均值或标准差。此外,当非平稳性随着土壤强度的小幅增加而不显著时,模型边界会显著影响影响的标准偏差和跳动距离,但对滑动体体积的影响很小。此外,大变形特征的平均值和标准偏差随着Su变化系数的增加而增加。本研究表明,土壤空间变异性的非平稳性会影响破坏起始阶段的破坏机制,从而影响滑动体的体积,其在失效后阶段控制滑动质量的动能并影响影响和跳动距离。
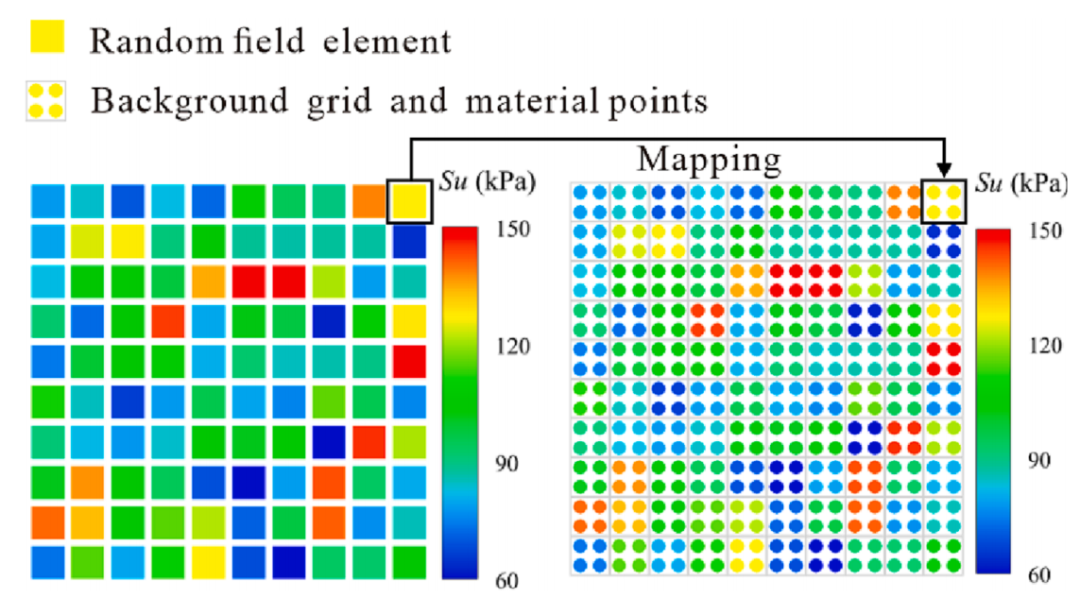
图:不排水强度空间变量与随机场元素和材料点映射的示意图。

图:不排水抗剪强度随机场的典型实现。

图:随机场作用下边坡的破坏机理。
文五:

有限变形岩土材料脆韧性破坏过渡的对流粒子域内插相场隐式物质点法
摘要:
提出了一种采用对流粒子域插值的相场隐式物质点法(PF-ICPDI)来模拟压敏岩土材料在有限变形条件下的脆韧性破坏转变。在该方法中,采用基于微力平衡定律和热力学第二定律的相场断裂公式作为非局部损伤函数进行弹塑性断裂分析。利用光滑的双屈服面塑性本构模型来评估压敏岩土材料的脆韧性破坏转变行为。通过引入有效相场应力并将总储存能量分解为弹性和塑性部分,建立了相场断裂模型和帽塑性模型的耦合效应。针对准静态弹塑性断裂有限变形问题,提出了一种能避免网格严重变形、提高数值稳定性的隐式材料点法。此外,在模拟大变形脆塑性失效过渡过程时,采用了对流粒子域插值技术来消除数值噪声,提高材料点跨越单元边界时的计算精度。采用交错增量迭代法求解耦合离散控制方程。通过几个具有代表性的数值例子证明了所提出的PF-ICPDI方法的准确性和能力,并讨论了主要材料参数对岩土材料相场脆性-韧性破坏转变模型的影响。

图:实体域的示意图

图:不同围压下平面应变压缩试验的等效塑性应变(a-g)和相场(h-n)轮廓

图:不同垂直位移下岩质边坡的等高线图




