流固耦合(fluid-structure interaction)研究
文一:

流体-结构相互作用模型
摘要:
柔性结构与浸没在其中或被其包围的流动流体的相互作用产生了丰富多样的物理现象,在许多工程领域都有应用,例如,机翼的稳定性和响应、血液通过动脉的流动、桥梁和高层建筑对风的响应,涡轮机和压缩机叶片的振动以及热交换器的振荡。为了理解这些现象,我们需要对结构和流体进行建模。然而,为了与本卷的总体主题保持一致,这里的重点是流体模型。此外,这些应用主要来自航空航天工程,尽管这些方法和基本物理现象有更广泛的应用。在本文中,我们强调了最近的发展和未来的挑战。为了提供上下文,本文首先描述了经历时间相关运动的流体的各种物理模型,然后讨论了线性和非线性模型之间的区别,时间线性化模型及其在时域或频域中的解,以及处理非线性模型的各种方法,包括时间推进,谐波平衡和系统识别。最后,我们对含时流动的模态特征进行了扩展处理,并基于流体模态的展开构建了降阶模型。重点是通过降阶模型、时间线性化和从动力系统理论中提取的方法,增强对物理的理解,并大幅降低计算成本
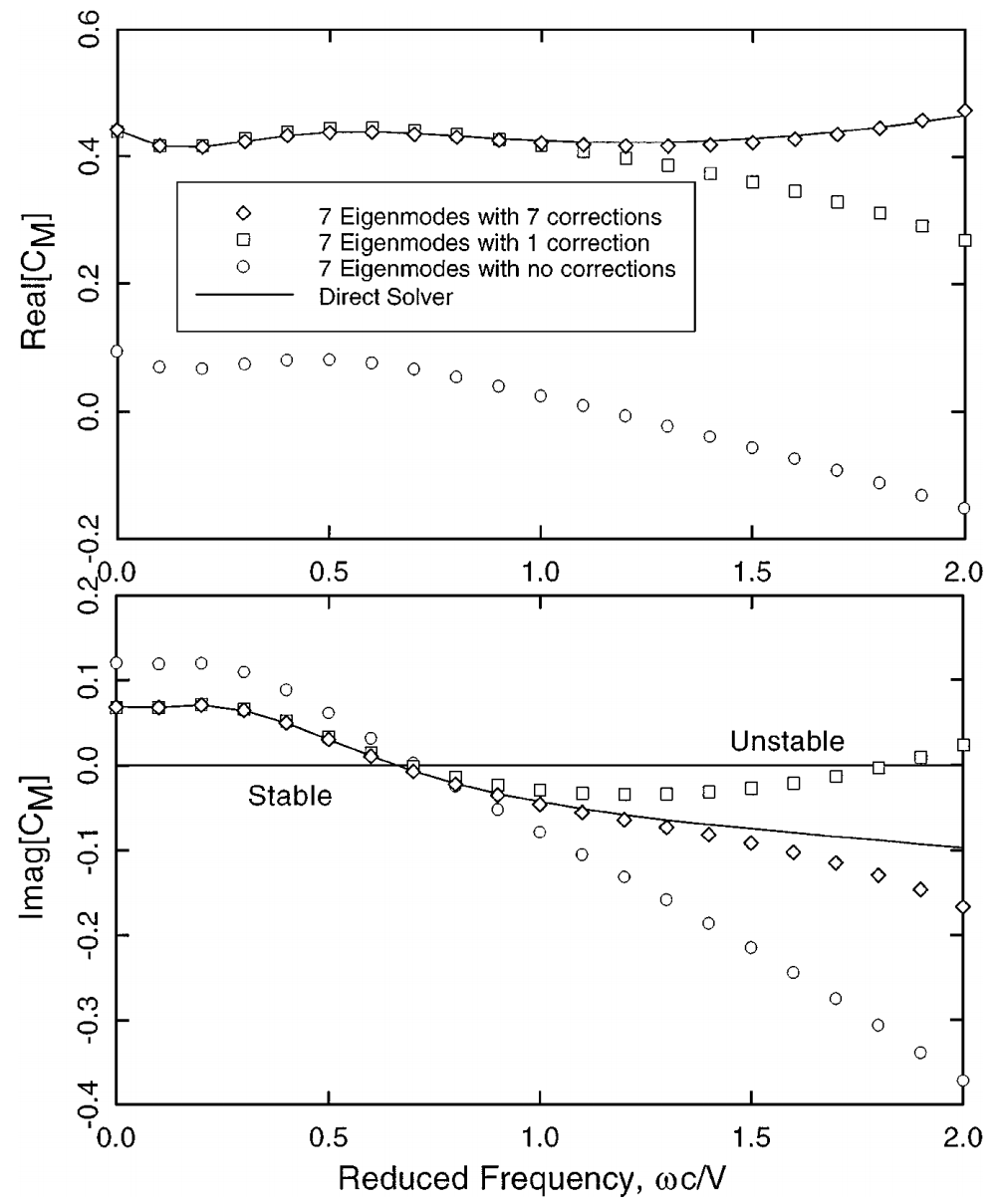
图:在一个降低的频率范围内,机翼围绕中弦附近的一个点俯仰的真实和假想(Imag)俯仰力矩。=62◦; σ=90◦
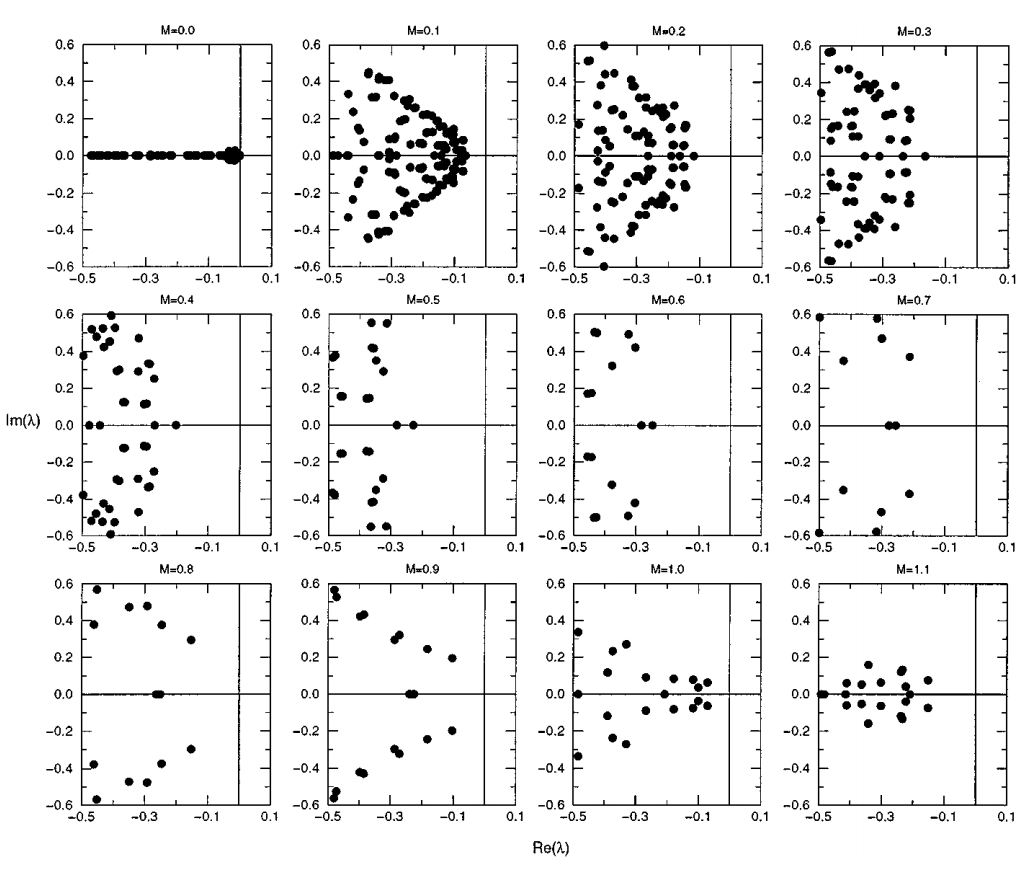
图:完整的空气动力学特征谱。真实;Im,虚数,M,马赫数。平板翼型(16×8目)

图:全谱和 ROM 气动特征谱的比较
文二:

大结构位移流体结构相互作用
摘要:
可变形结构内部粘性流动的计算在保证变形结构的运动协调性方面遇到了很大的困难流体结构界面和更新领域的几何。本文提出了克服这些问题的考虑流体和结构作为一种独特的连续介质,以固定的参考构型进行研究。结果导致的问题是然后通过对运动学允许的测试函数的空间进行加性分解,将其分解为流体和结构部分这种方法以完全拉格朗日的方式处理结构,并使用相关的任意拉格朗日欧拉(ALE)公式这种策略有三个优点,本文将详细介绍。采用隐式的、稳定的、能量守恒的时间积分格式进行时间离散,并用简单的、迭代的非线性方法求解耦合算法;流体和结构问题可以用独立的有限元空间来近似;最新的几何精确非线性壳模型可以用于结构。该方法已在工业 CFD 程序中得到实现,并在工业液压系统仿真中得到了验证本文最后介绍了减震器。
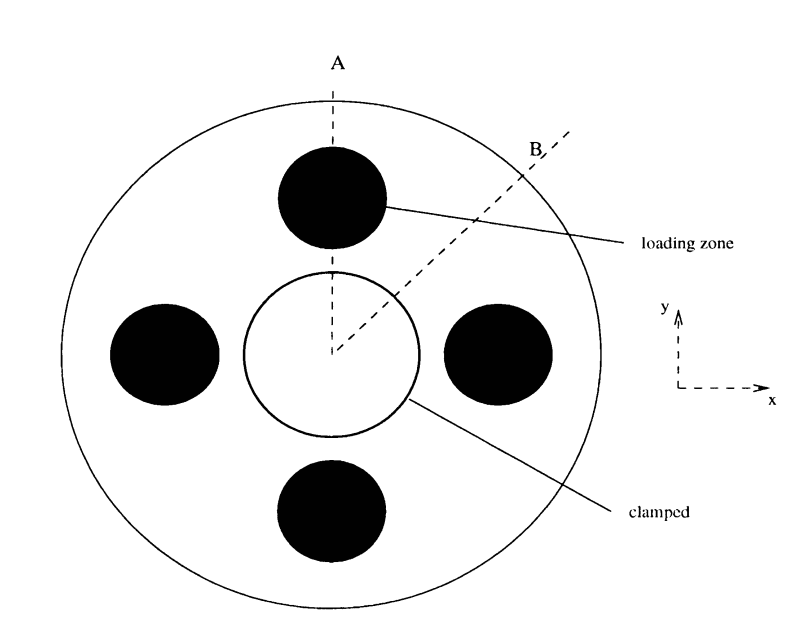
图:阀门八分之一的几何形状和负载。
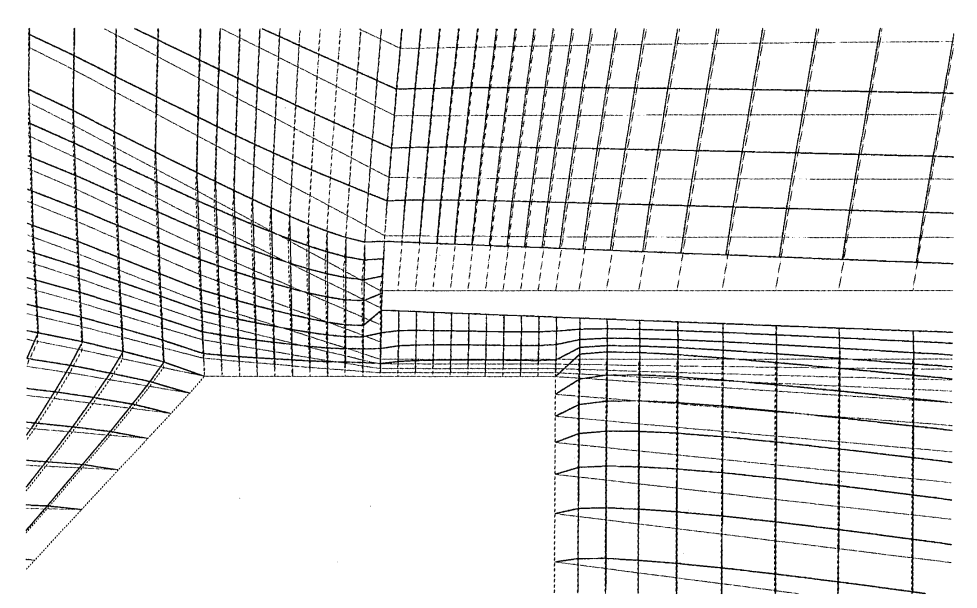
图:网格更新: 在对称平面上的轨迹,颜色较暗的是通过显式全局算法得到的更新。
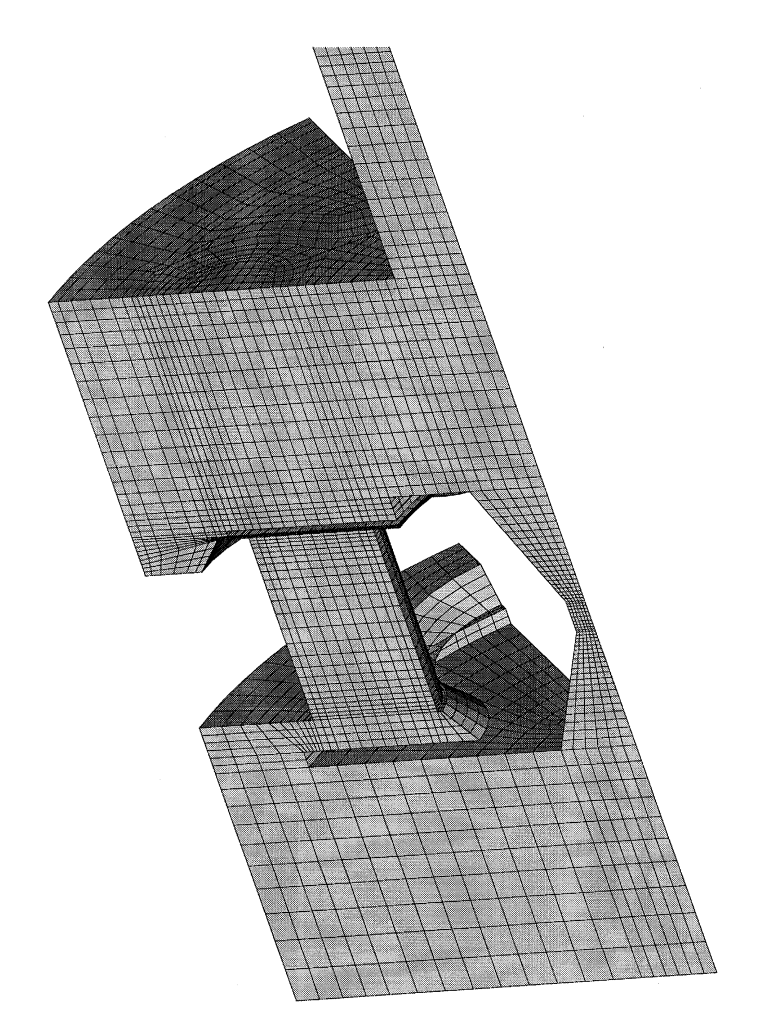
图:液体结构域(液体部分)网格: 结构域18500个细胞的1/8。观察永久性中心孔。

图:对称平面内最大流量下的压力场。
文三:

流体-结构相互作用的时空有限元整体方法
摘要:
本文提出了流体-结构相互作用问题的同时求解程序。结构运动用几何非线性弹性动力学描述。流体由不可压缩的Navier-Stokes方程建模。将时空有限元方法应用于连续体,导致流体和结构使用速度变量的几乎均匀离散化。为了加强界面处的动量守恒和几何连续性,引入了耦合条件的加权残差公式。将流体、结构和耦合条件下的离散模型方程建立在一个单独的方程组中。非线性系统和流体网格运动在一个迭代循环中求解。薄膜颤振和涡流激励板振动的二维例子证明了该方法的有效性。
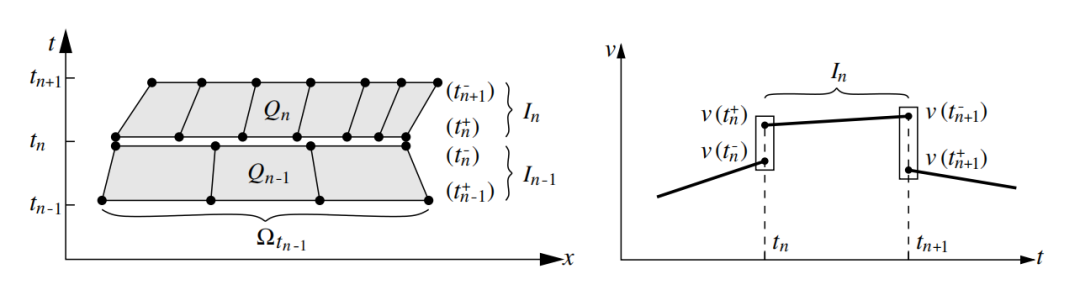
图:移动时空网格与时间不连续插值。
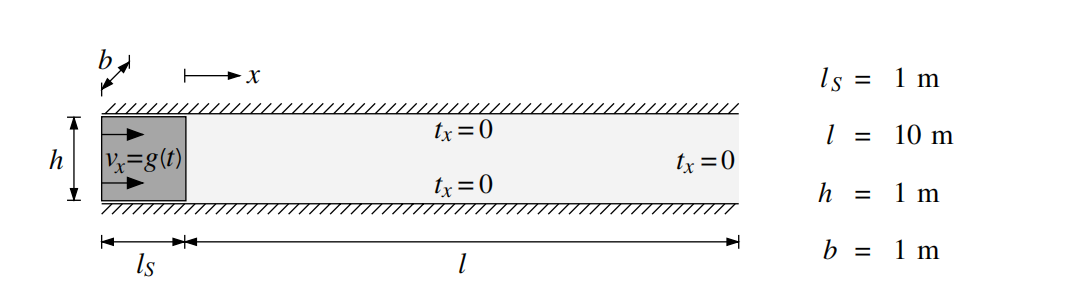
图:活塞示例的系统配置
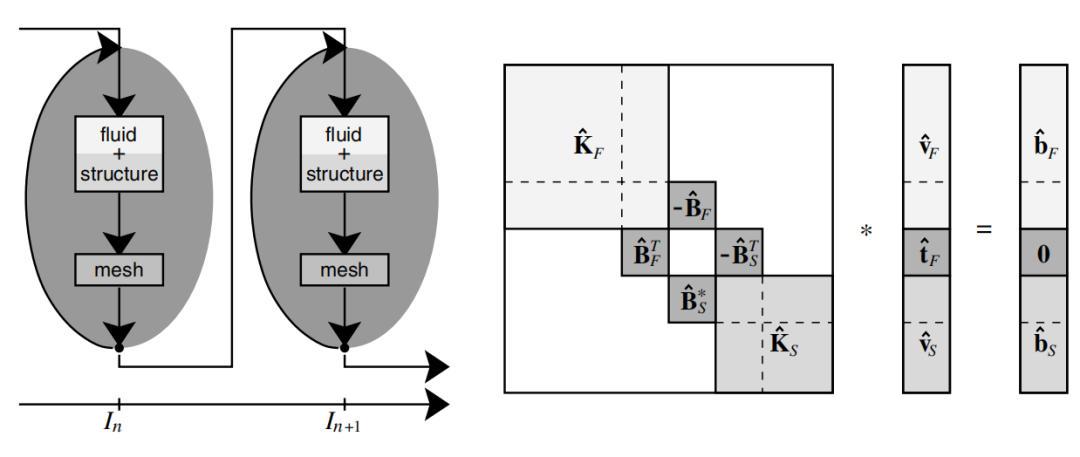
图:联立求解程序和耦合方程组。
文四:

内部生理流动中的流体-结构相互作用
摘要:
我们选择性地回顾了在分析几个生理学和生理学启发的流体-结构相互作用问题方面的最新进展,我们的目的是解释导致观察到的行为的潜在物理机制。具体来说,我们讨论了最近对可折叠管中自激振荡的研究,主要集中在对理想化模型系统Starling电阻器的研究上,Starling电阻器是大多数实验室实验中使用的设备。接下来,我们将回顾一种特殊的生理学、流诱导振荡的研究:发声过程中的声带振荡。最后,我们讨论了肺气道的关闭和重新开放,以及涉及气道液体衬里的生理流体-结构相互作用问题。
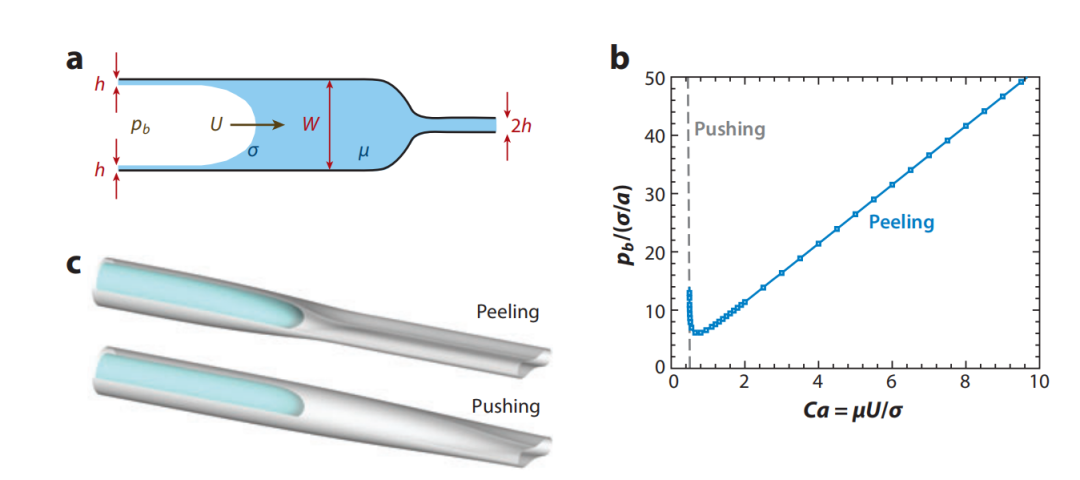
图:(a) Gaver等人(1990)的肺气道重新开放模型示意图。空气指稳定地传播到塌陷的弹性管(或2D通道)中,该管充满粘度为μ和表面张力为σ的粘性流体。传播的手指打开气道,将液体重新分配到薄的液体衬里中。
(b) 典型的压力-流量关系,显示了以给定速度U将手指驱动到未变形半径a的塌陷3D管中所需的压力pb。虚线显示了Hazel&Heil(2003b)对低速推动分支行为的渐近预测。(c) 在剥离和推动状态下管壁和气液界面的代表性形状。

图:(a) 喉部素描,显示真实和虚假的声带。声带有一个复杂的内部结构,这里分为两个主要区域:覆盖层和身体,覆盖层包含高度柔性的粘膜表层,身体包含用于调节声带形状和张力的肌肉纤维。
(b) 图示振荡期间声带几何形状变化的示意图,当声带分离/接近时,导致声门会聚/发散。(c) 声带在空泡模式下的三个最低阶的图解。模式2和模式3的流诱导同步和叠加可以产生如图b所示的声带振荡。
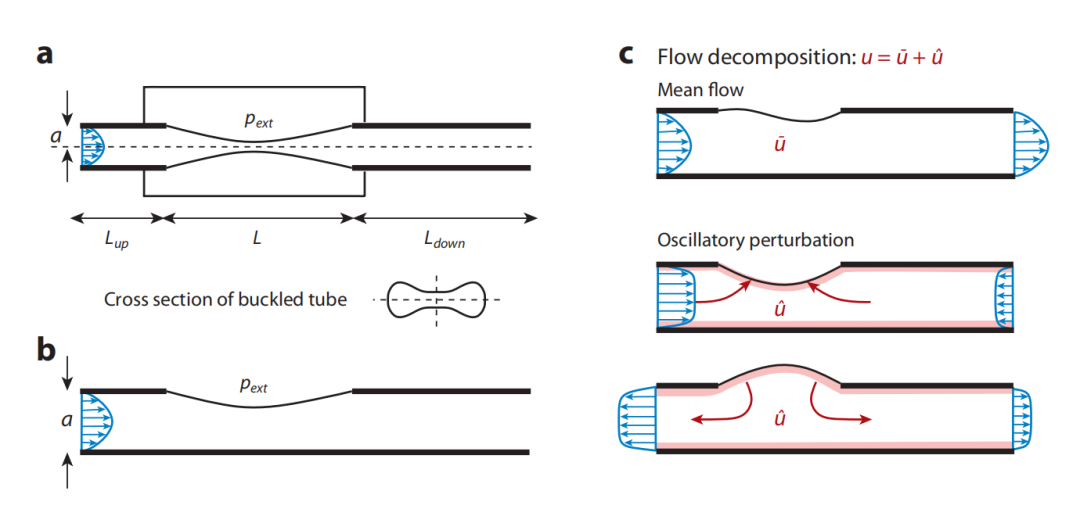
图:(a) Starling 电阻器的示意图,这是一个薄壁弹性管,安装在两个刚性管上,并封闭在一个压力室内,以及(b)它的二维等效物,一个通道,其中一个壁的一部分被预应力弹性膜取代。(c)晃动机制的说明。将流动分解为平均分量 u 和振荡分量 u。壁面运动在上游或下游刚性截面上产生振荡晃动流动。在足够高的频率下,晃动流有一个钝的无粘核心,在壁面附近有薄的斯托克斯层
文五:

流体与结构相互作用问题的ALE公式
摘要:
任意拉格朗日-欧拉(ALE)有限元方法因能够独立于材料几何结构控制网格几何结构而备受关注。在“uid”结构相互作用问题中,结构附近的uid网格经历了大量变形并变得不可接受的畸变,这将时间步长驱动到非常小的值来进行显式计算,ALE方法或重新分区用于为“uid域”创建一个新的无畸变网格,这允许计算继续进行。ALE和重分区算法的数学基础很简单,但由于与处理任意网格相关的繁琐的地质测量计算,它们的实现很复杂。在本文中,我们将ALE概念应用于“流体”-结构相互作用问题。我们将解释该方法的基本思想,并给出控制网格失真的可能方法。给出了一个学术问题和一个工业问题的结果。
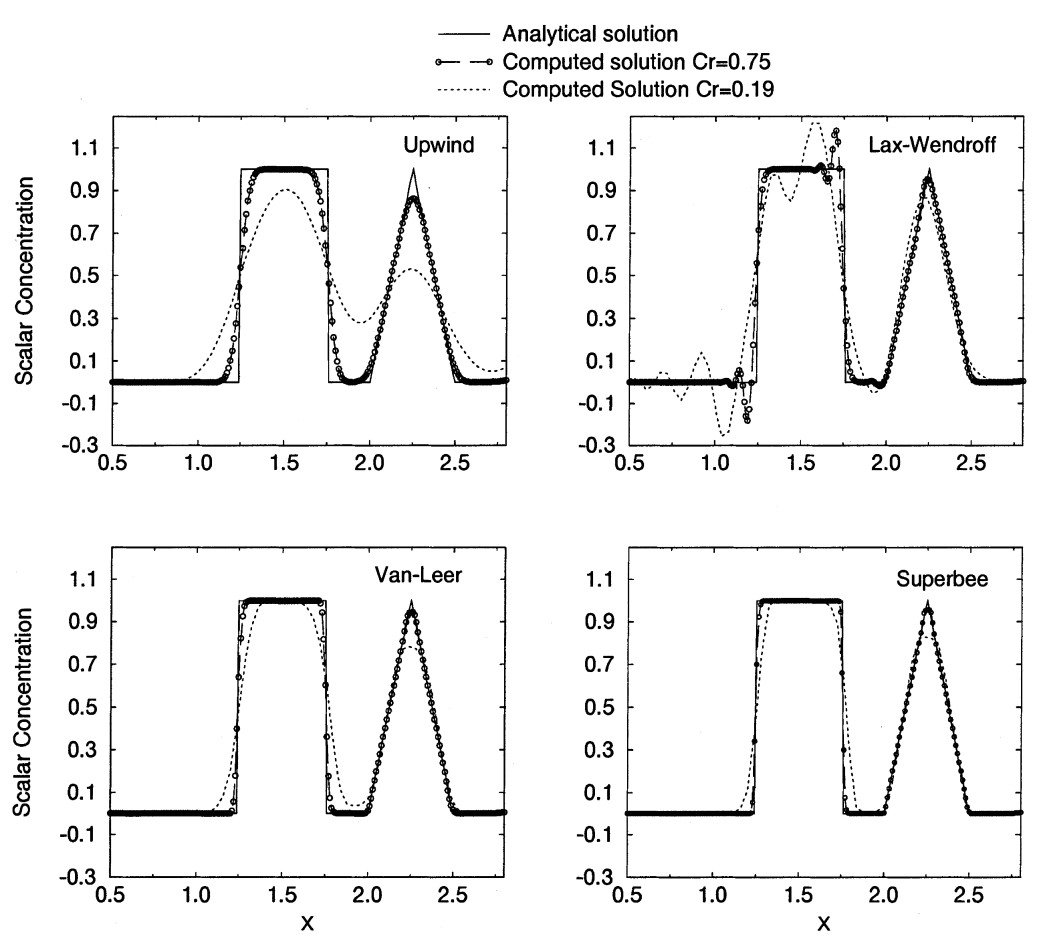
图:不同格式的数值结果与精确解的比较。
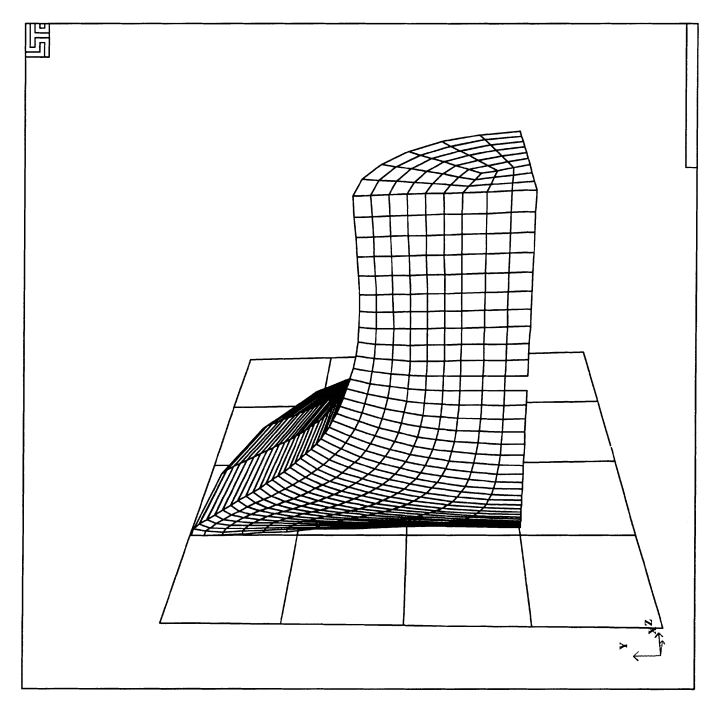
图:泰勒杆冲击的拉格朗日公式
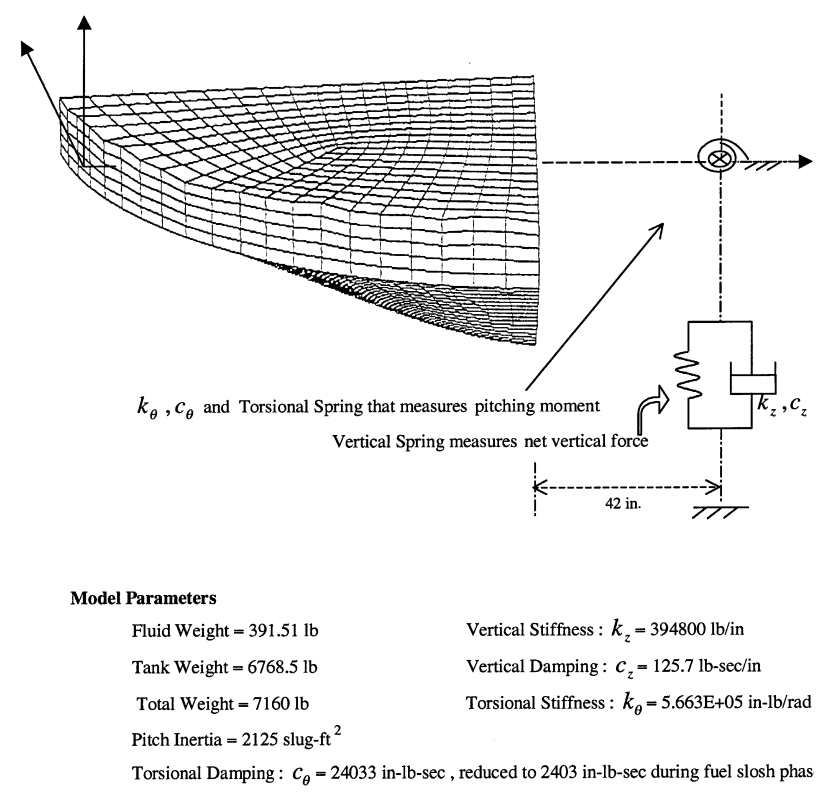
图:分析方法和油箱模型。油箱大约有一半的油。

图:流体±结构相互作用。到达板的球面压力波




