固体大变形模拟研究的最新进展
文一:

织构和孪晶对镁合金实心杆扭转行为的影响: 与单轴拉伸/压缩比较的晶体塑性方法
摘要:
采用具有孪晶和去孪晶方案的弹粘塑性自洽模型,结合特定扭转的有限元方法,对镁合金AZ31实心棒在不同初始织构(包括理想基底、轧制、挤压和随机)下的变形行为进行了建模。除了具有几乎均匀变形(拉伸和压缩)的载荷外,还研究了具有非均匀变形的载荷路径,特别是在自由端和固定端扭转的情况下。模拟表明,随着初始织构和加载路径的不同,变形机制发生了显著变化,导致应力-应变响应、Swift效应和变形织构发生变化。特别是,我们的晶体平面模型很好地捕捉到了扭转条件下固体棒内部应力和孪晶体积分数的不均匀分布。这一点尤其重要,因为我们的扭转特定晶体塑性模型提供了一种数值工具,可用于通过实心棒的扭转来调节梯度孪晶结构,以提高镁合金的力学性能。

图:实心扭杆力学模型的示意图和相关模型数量的定义。

图:根据 AZ31镁合金实心棒在(a)拉伸、(b)压缩和自由端扭转下的{0001}极图,在考虑孪生和(d)没有考虑孪生的情况下,在(a)拉伸、(b)压缩的轴向应变 ε = 0.15和自由端扭转(c)的剪切应变 Γ = 0.7。注意到(c)和(d)中的极图同时在 θ-r 平面和 θ-z 平面上出现。
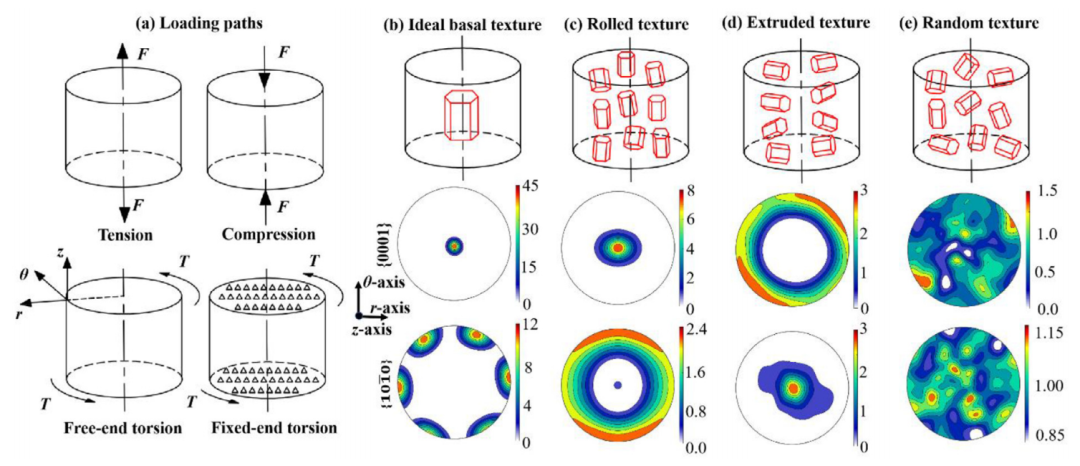
图:在(a)拉/压和自由/固定端扭作用下加载的实心杆试件示意图。镁合金 AZ31B 实心棒的初始(b)理想基础,(c)轧制,(d)挤压,(e)按{0001}和{1010}极图计算的随机织构。
文二:

基于显微结构的大应变塑性变形多尺度建模——将全场晶体塑性谱求解器与隐式有限元求解器耦合
摘要:
我们在隐式有限元(FE)框架中提出了全场晶体塑性模型的全嵌入实现,该组合实现了模拟大应变塑性变形的多尺度方法。在宏观有限元模型的每个积分点,一个基于快速傅立叶变换(FFT)的光谱求解器从下面的全场多晶代表体积单元(RVE)模型中输入均匀化响应,该模型通过使用晶体塑性本构公式求解。在开源软件DAMASK中实现的现象硬化定律和基于位错密度的硬化模型都被用来提供中尺度的本构响应。FE-FFT模型的准确性已经通过FCC多晶体的几种加载场景的单元测试进行了基准测试,包括简单拉伸、简单压缩和简单剪切。应用多尺度模型模拟了四种应用情况,即FCC板的平面应变变形、FCC圆柱体的压缩、HCP棒的四点弯曲和双相钢的梁弯曲。证明了该模型在预测中尺度微观结构演化以及宏观和中尺度力学响应方面的卓越能力。
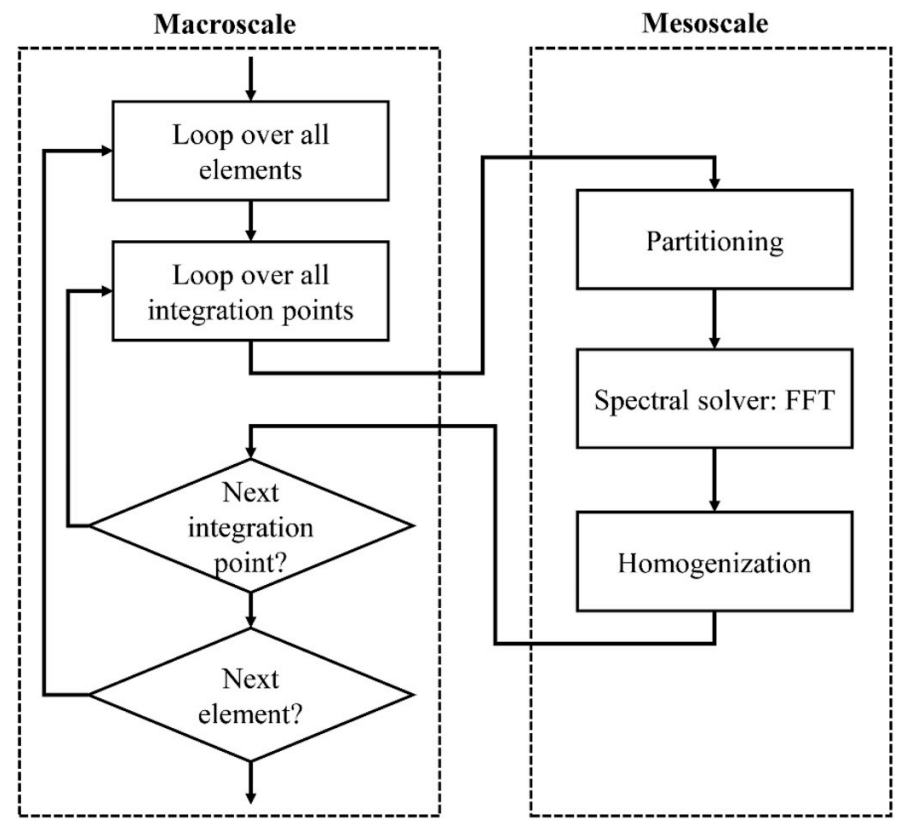
图:在FEM中嵌入频谱求解器的多尺度模型各阶段的流程图。
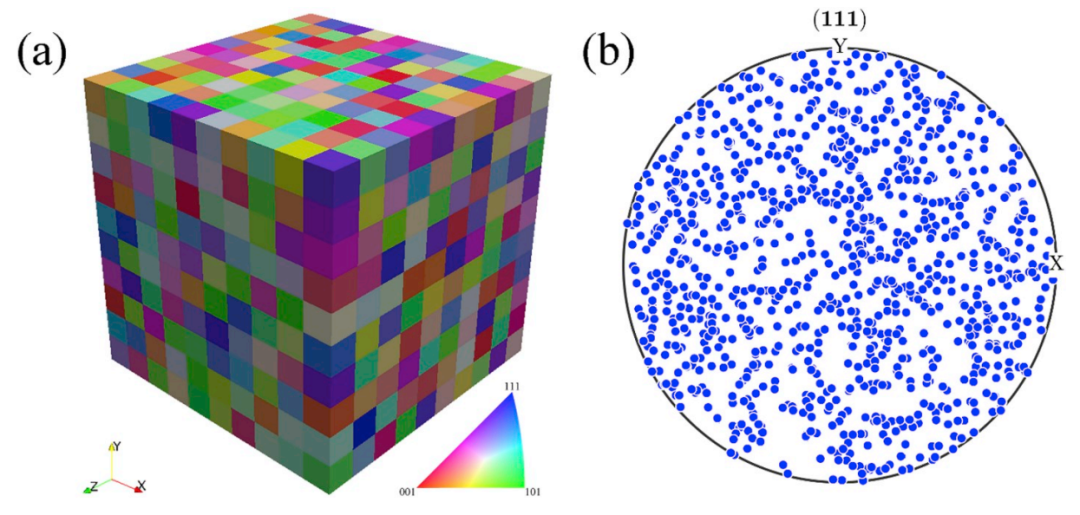
图:(a)根据沿 Z 方向的逆极图(IPF)着色的代表性体元素(b)分配给 RVE 的随机纹理(每个方向仅显示一个极点)。
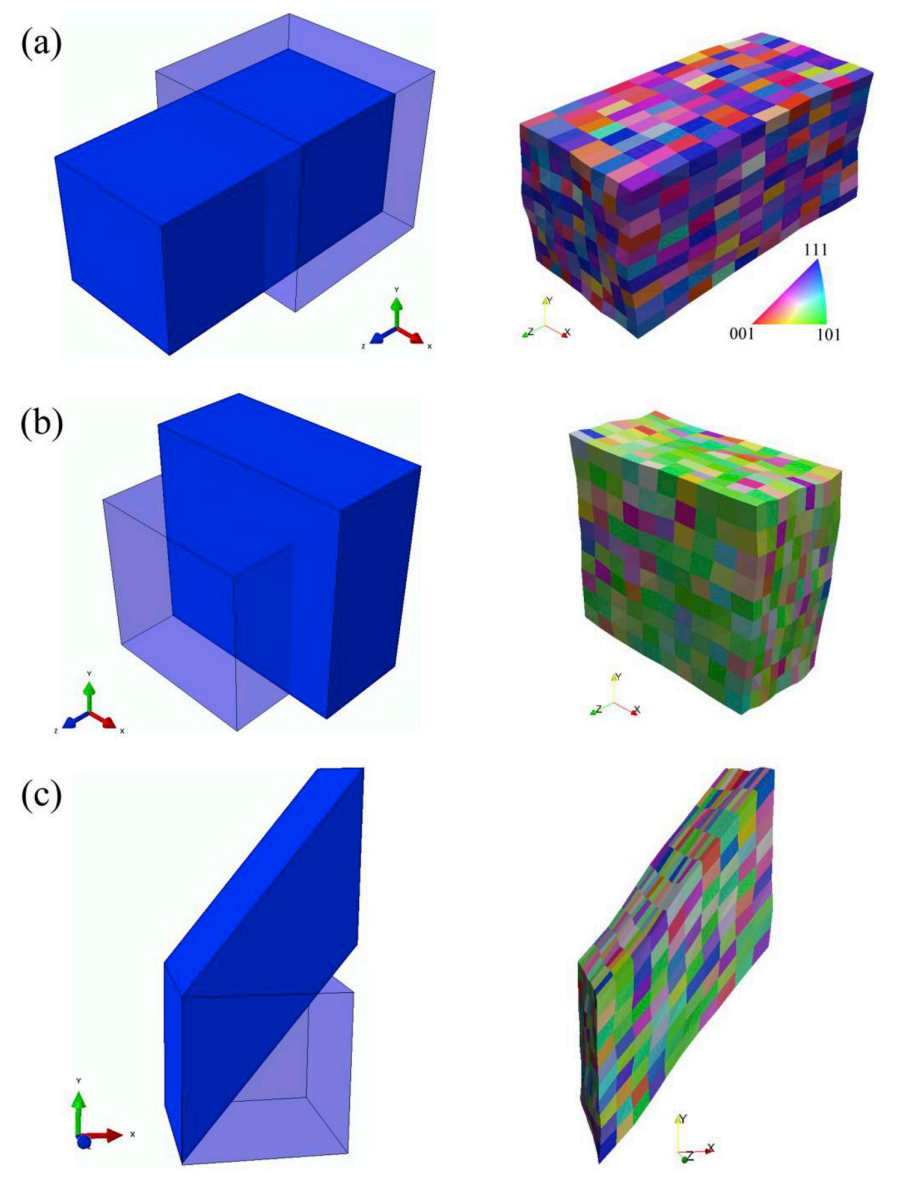
图:单元试验(a)简单拉伸(b)简单压缩(c)简单剪切,显示单元形状和变形后嵌入的 RVE。RVE 根据沿参考 Z 方向的 IPF 着色。
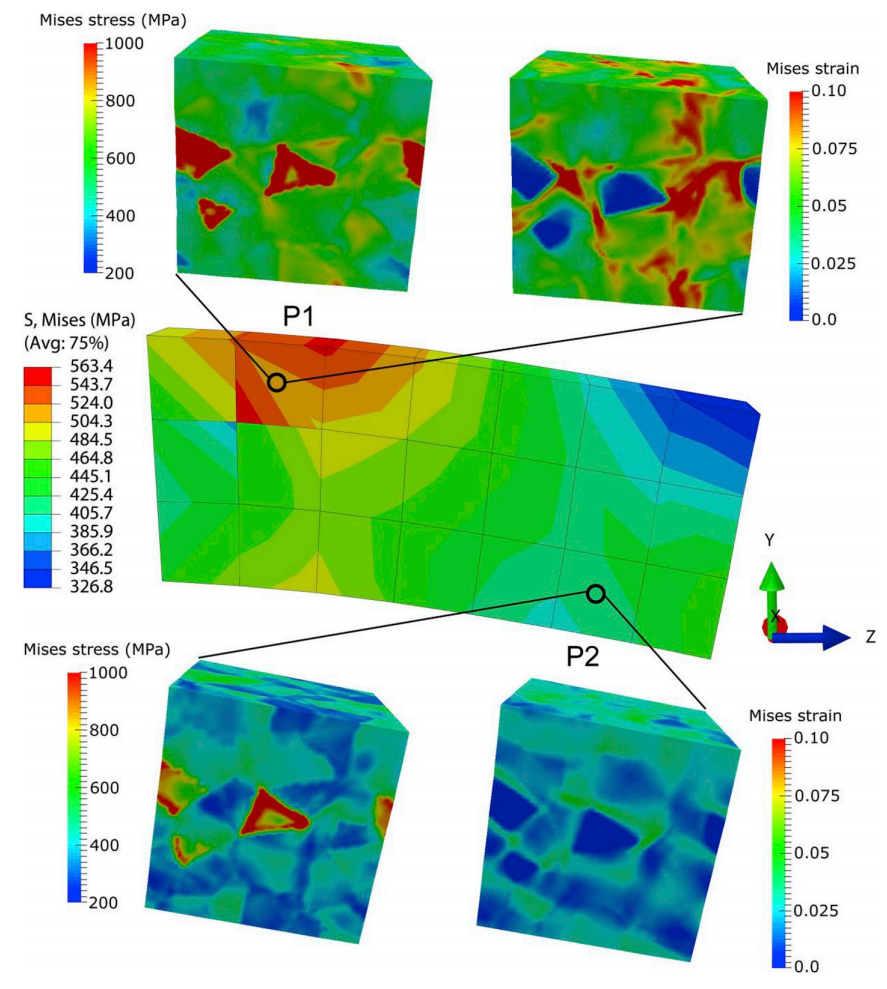
图:用ABAQUS-DAMASK模拟圆形刚性模具纯铝的平面应变变形。(a)最大主应变(b)剪切应变分量LE13的分布。

图:在每个积分点分配了不同RVE的圆柱体的有限元模型。圆柱体的上半部分配有细粒度RVE,而下半部分配有粗粒度RVE。RVE根据IPF沿Z方向进行着色。
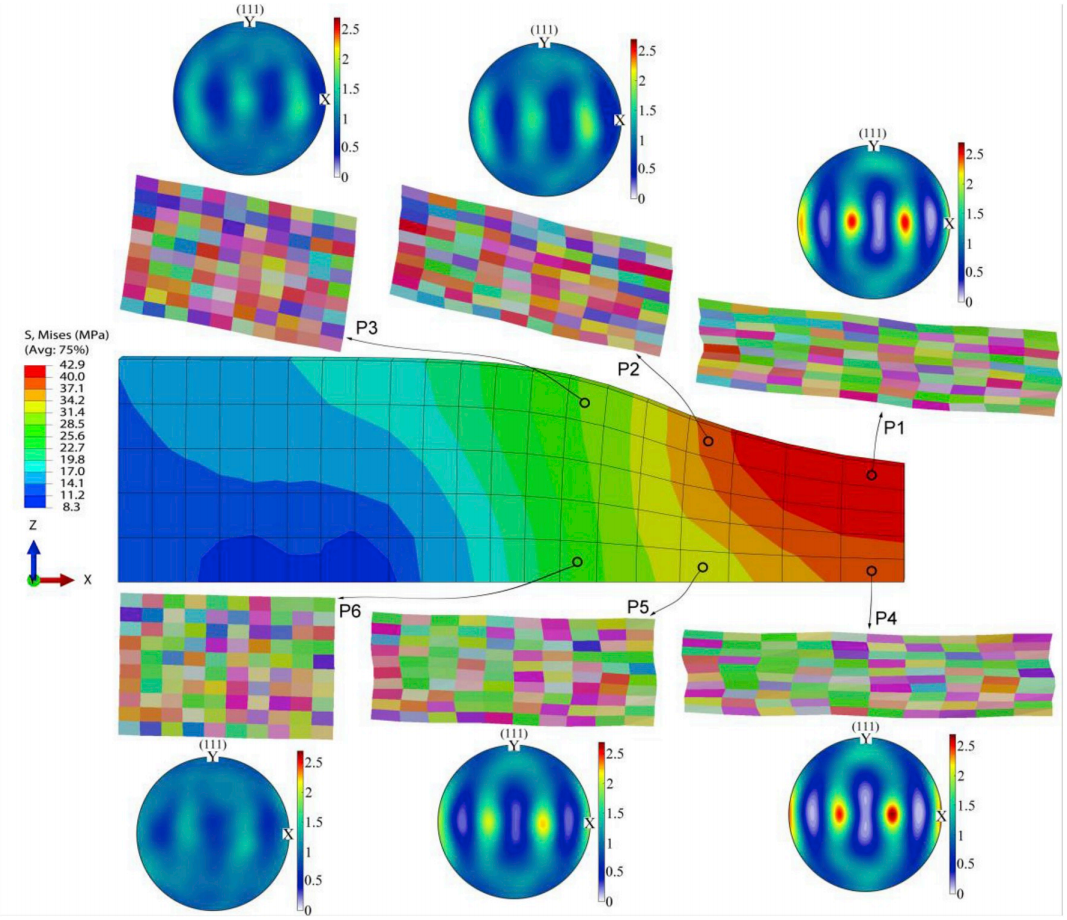
图:纯铝平面应变压缩的 ABAQUS-DAMASK 模拟: 显示在 x-z 平面上的 Von Mises 应力分布,以及嵌入 RVE 的最终形状和相应的晶体结构,显示在所指定的六个位置的 x-y 平面上的投影极图。

图:圆形刚性模具纯铝平面应变变形的 ABAQUS-DAMASK 模拟。(a)最大主应变(b)剪应变分量 LE13的分布。
文三:

添加制造的316L不锈钢的速率和温度相关塑性:表征、建模和在壳晶格破碎中的应用
摘要:
对通过选择性激光熔炼获得的添加不锈钢316L的准静态和高应变速率响应进行了数值和实验相结合的研究。实验程序包括单轴拉伸、剪切、缺口拉伸和迷你Nakazima试样的实验,涵盖了广泛的应力状态和应变速率(从10−3到103/s)。建立了一个具有Swift-Voce硬化和Johnson-Cook速率和温度依赖性的各向异性二次塑性模型,以描述不同应力状态和应变速率下组成基体材料的行为。在弹性各向同性壳格结构上进行了低和高加载速度下的压缩实验,以进一步验证已确定的塑性模型在结构应用中的有效性。研究发现,所选择的塑性模型能够很好地描述不同速度和方向加载的光滑壳晶格的反作用力和变形模式。实验表明,无论加载速度如何,添加制造的壳晶格都能够维持60%以上的宏观压缩应变,而不会出现细胞壁的可见断裂。与相同质量的板晶格结构的结果进行比较,阐明了壳晶格的巨大能量吸收潜力。
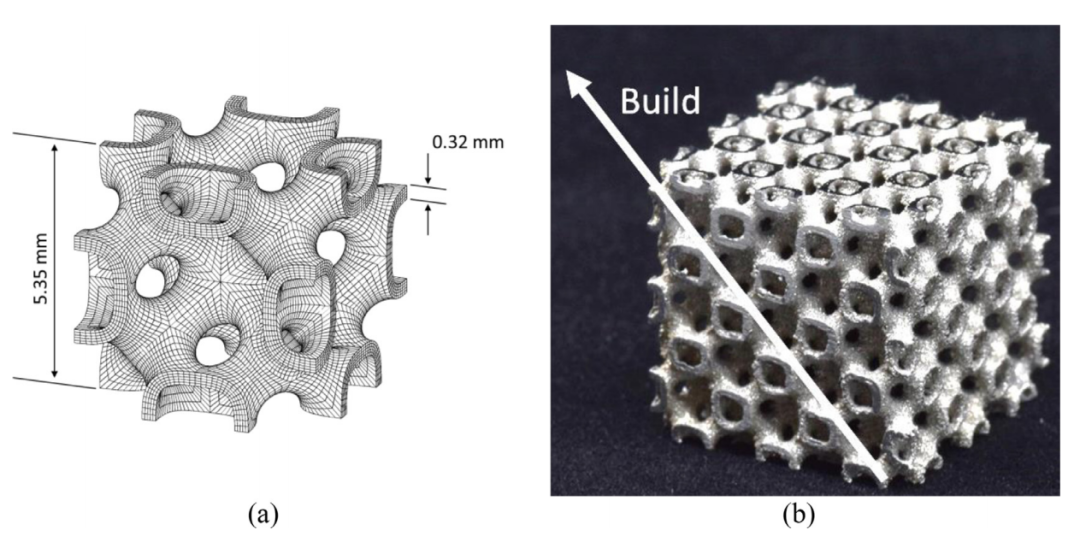
图:(a)单元网格拓扑与有限元网格的壳格。(b)未经测试的单轴压缩样本(单元格的3 × 3 × 3堆叠)的视图,这些样本是用316L 选择性激光熔化制造的。

图:在两种加载速度下对45°取向的光滑壳晶格进行压缩实验的结果:在(a)低速和(b)高速下,选定应变水平为10%-50%时的变形过程图片。

图:(a) 每个薄板的高度为170mm、宽度为210mm、壁厚为1mm的平行薄板结构的设计。0°方向与打印方向对齐。(b) 从顶部看,打印矩形块的倾斜特写视图。

图:从(c)添加制造的块体的(a)顶部、(b)正面和(d)侧面提取样品的组成材料的EBSD图像。沿印刷方向观察到细长晶粒,平均晶粒尺寸约为20μm,晶粒尺寸至少有一个数量级的扩展。

图:中速下的实验结果
文四:

大变形弹塑性的拉格朗日力学和隐式材料点法
摘要:
物质点法非常适合于建模涉及大变形的问题,而传统的基于网格的方法 会很困难。然而,就该方法的平衡公式而言,总拉格朗日方法和更新拉格朗日方法分别是不合适的和不理想的。这是由于材料点方法的基函数,特别是基函数的导数,通常在未成形的、有时是规则的背景网格上定义。使用材料点处的变形来映射基函数空间导数是可能的,但这引入了额外的算法复杂性和计算费用。本文提出了一种新的拉格朗日平衡表述,它是材料点法的理想表述,因为它在加载步骤开始时满足未变形背景网格上的平衡。该公式是使用准静态隐式算法实现的,该算法包括一致切线的推导,以实现全局平衡迭代的最佳收敛。该方法应用于许多大变形弹塑性问题,特别关注该方法与标准、广义插值和CPDI2材料点法的分析解的收敛性。对于广义插值方法,研究了不同的域更新方法,结果表明,在特定的简单变形场下,所有现有方法都是退化的。提出了一种新的域更新方法来克服这些问题。所提出的材料点法框架可以应用于所有现有的材料点方法,并用于隐式和显式分析,但其优点主要与前者有关。
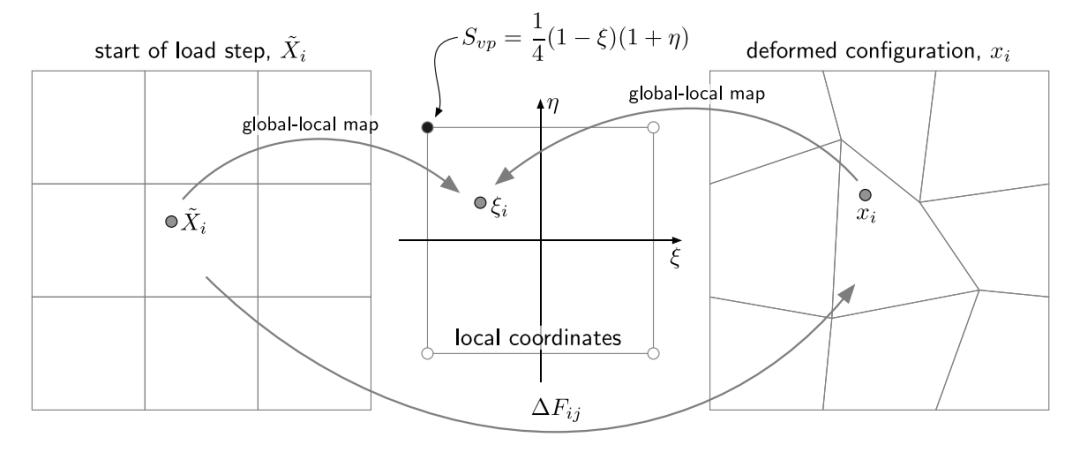
图:变形框架的全局-局部映射和加载步骤开始时的配置
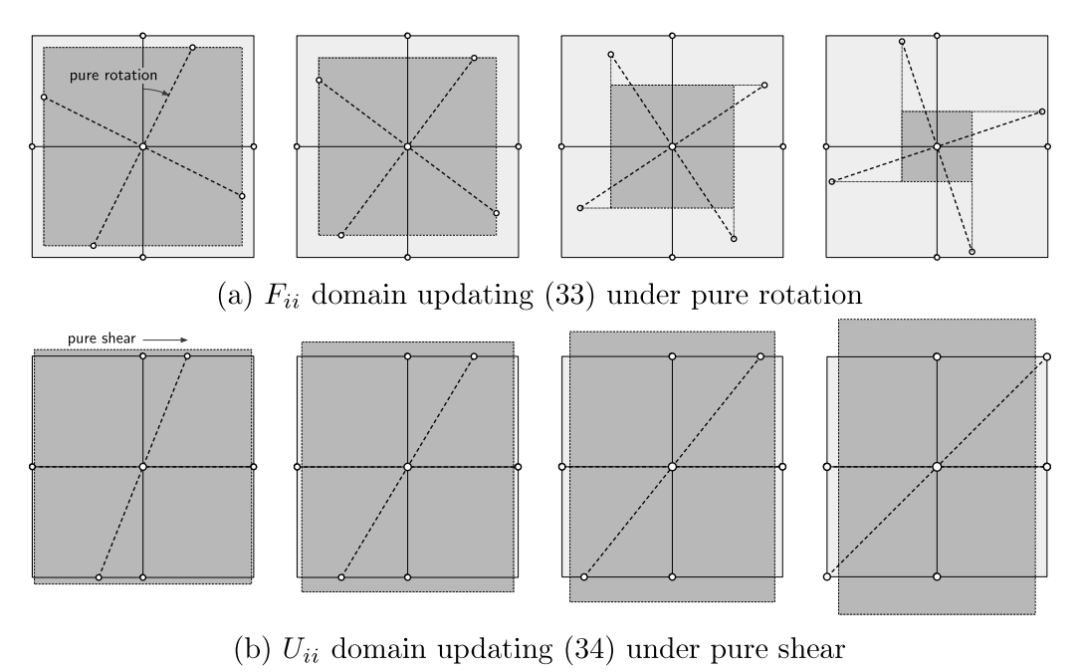
图:不同变形模式下的域更新过程,其中浅灰色和深灰色阴影区域分别为原始域和更新域。
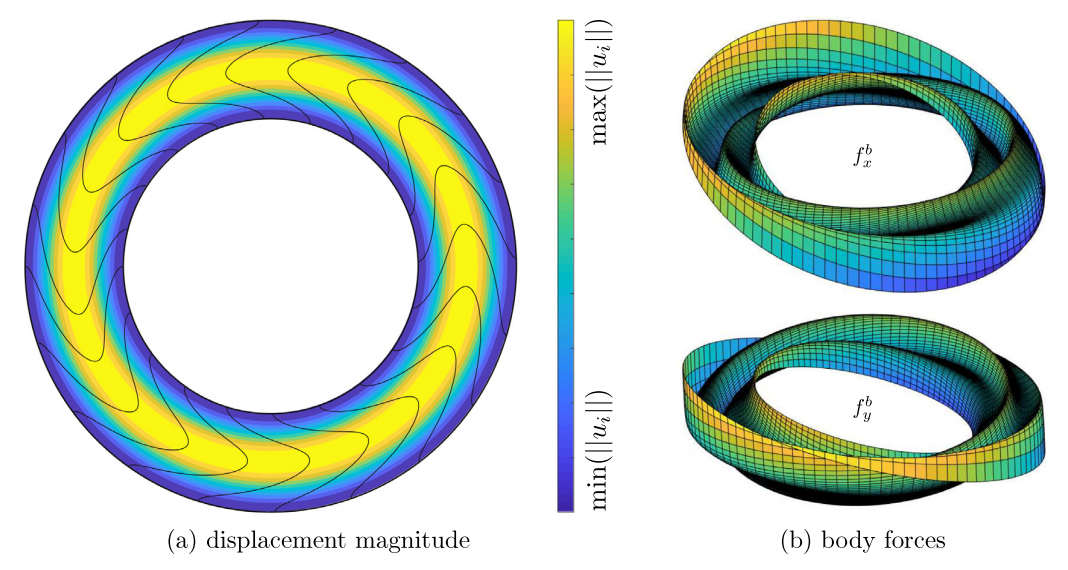
图:弹性环: 位移场与体力分量。对于身体的力,最大的正值和负值分别是黄色和蓝色。

图:弹塑性坍塌:根据σyy着色的变形材料点位置。
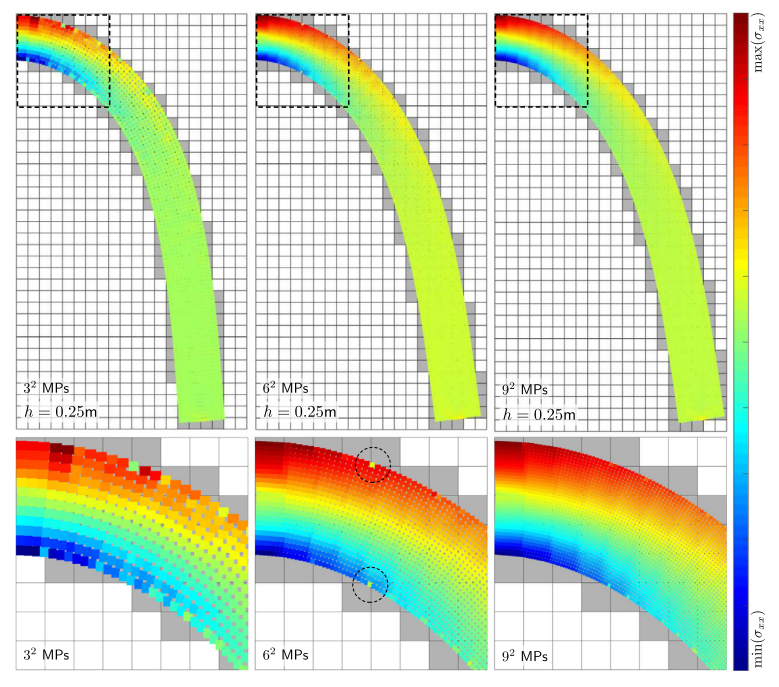
图:弹性梁: 变形材料的点位置,根据 σxx 着色,h = 0.25 m。活动背景网格单元已被阴影灰色。
文五:

回顾泰勒冲击试验: 高应变率下金属塑性参数的确定
摘要:
泰勒冲击试验是表征金属在高应变速率(高达105 s-1)下塑性行为的最简单实验方法。在此,圆柱形杆被冲击在刚性固定砧上,并且通过将实验获得的杆变形与其理论对应物进行比较来估计动态屈服强度。尽管这是一个简单而有力的概念,但到目前为止,缺乏一个全面的理论模型(将材料本构关系与杆的变形模式联系起来)限制了泰勒冲击试验在材料表征中的使用。在本研究中,重新审视了泰勒冲击试验,并试图建立一个有效确定金属本构参数的反框架。逆分析是通过扩展卡尔曼滤波器技术进行的,其中基于Chakraborty等人(2015)中给出的推导来构建正向模型。与通常的做法不同,为了更好地估计材料常数,变形时间历程也包含在本逆公式中。为了进行演示,考虑了五种不同的应力模型,即Johnson–Cook模型、Zerilli–Armstrong模型、Steinberg–Cochran–Guinan–Lund模型、机械阈值应力模型和Preston Tonks Wallace模型。估计的参数与参考值基本一致。结果表明,本次尝试最明显的特点是,一次泰勒检验就足以以合理的精度确定参数
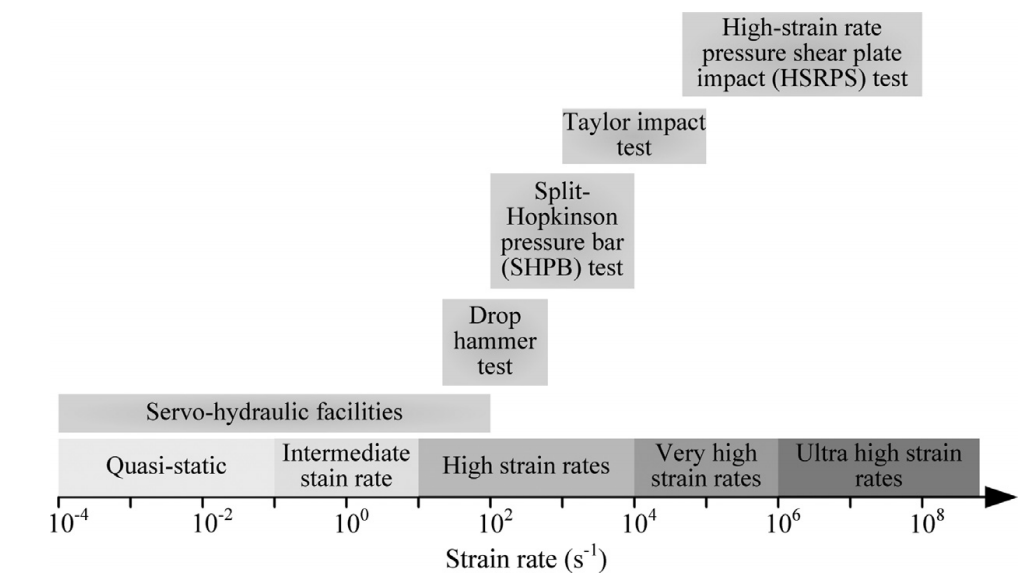
图:确定不同应变率下材料本构参数的实验方法

图:假定泰勒试样的变形形状

图:泰勒冲击试验




