应用数学与机器学习(Machine Lerning)的基础研究
文一:

DeepXDE: 求解微分方程的深度学习库
摘要:
深度学习在各种应用中取得了显著的成功,然而,它在解偏微分方程(PDE)中的应用是最近才出现的。在这里,我们提出了物理知情神经网络(PINN)的概述,其中嵌入了一个偏微分方程的损失的神经网络使用自动微分。PINN 算法简单,适用于不同类型的偏微分方程,包括积分微分方程、分数阶偏微分方程和随机偏微分方程。此外,从实现的角度来看,PINN 解决反问题和解决正问题一样容易。为了提高 PINN 的训练效率,提出了一种新的基于残差的自适应细化(RAR)方法。出于教学原因,我们将 PINN 算法与标准有限元分析进行了比较。我们还介绍了一个用于 PINN 的 Python 库 DeepXDE,它既可以作为教学工具使用,也可以作为解决计算科学与工程问题的研究工具。具体来说,DeepXDE 可以解决给定初始条件和边界条件的正问题,以及给定一些额外测量的反问题。DeepXDE 支持基于构造实体几何技术的复杂几何域,并使用户代码更加紧凑,与数学公式非常相似。我们介绍了 DeepXDE 的用法和它的可定制性,并通过五个不同的例子展示了 PINN 的性能和 DeepXDE 的用户友好性。更广泛地说,DeepXDE 为新兴的科学机器学习领域的更快发展做出了贡献。
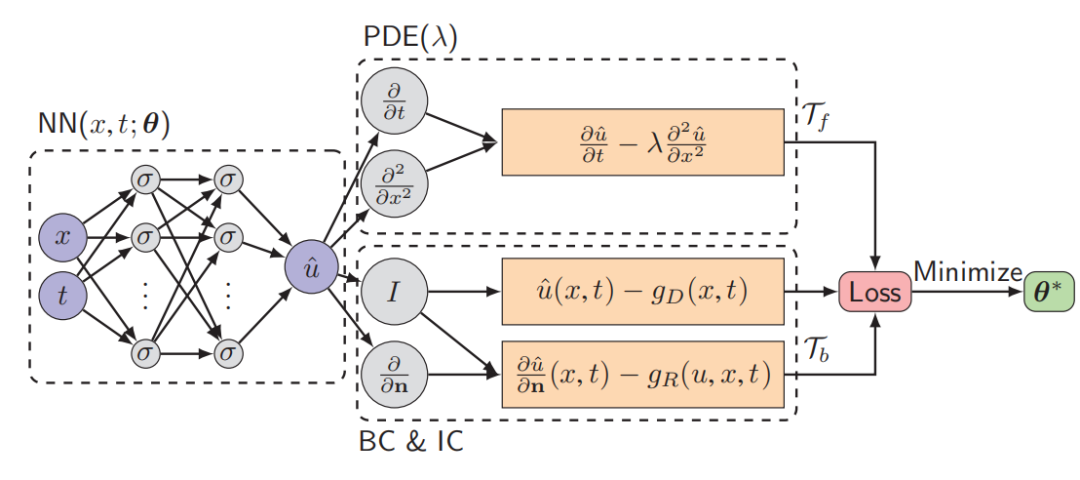
图:解决扩散方程的 PINN 示意图

图:训练过程中各频率振幅的收敛性。
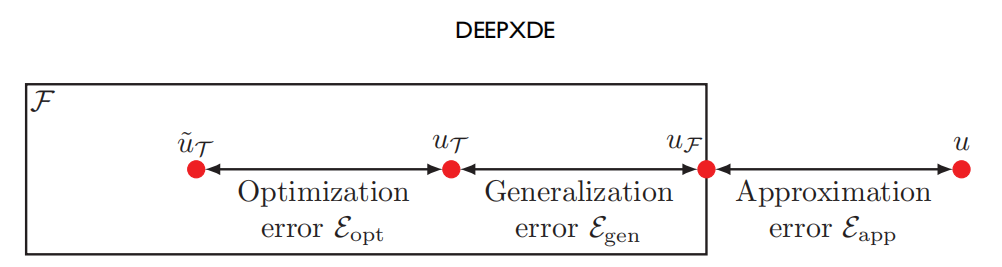
图:PINN错误说明
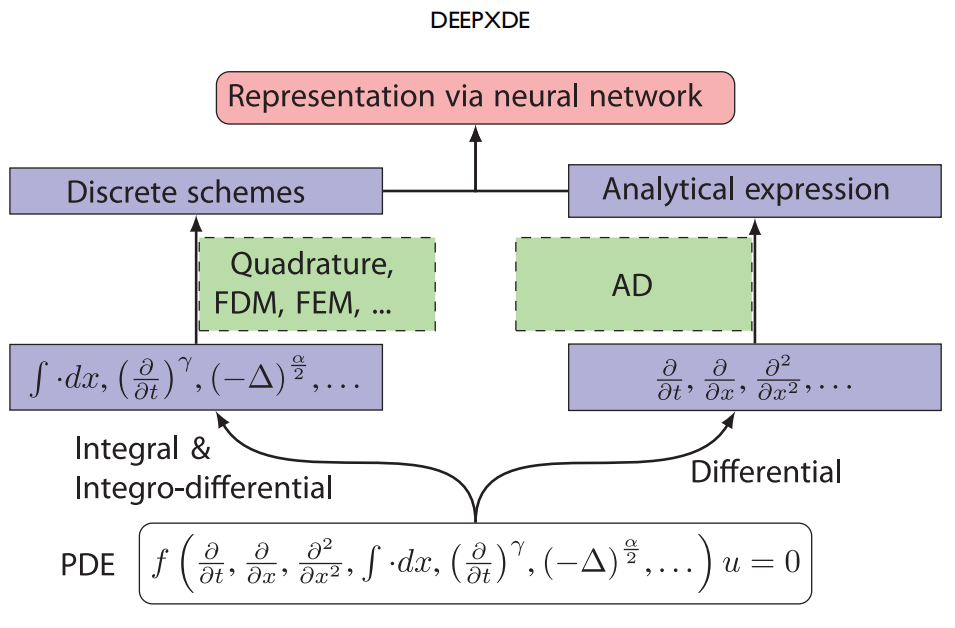
图:说明用于求解IDE的PINN算法的修改的示意图。

图:PINN溶液与使用光谱元素法(SEM)获得的溶液的比较。
文二:

随机微分方程数值模拟算法简介
摘要:
介绍了随机微分方程数值方法的实用性和易用性。假设读者熟悉确定微分方程的欧拉方法,并且至少对随机变量的概念有直观的感觉;然而,我们对高级概率论或随机过程没有任何了解。本文围绕10个MATLAB程序构建,涵盖的主题包括随机积分、Euler–Maruyama方法、Milstein方法、强收敛性和弱收敛性、线性稳定性和随机链式规则。
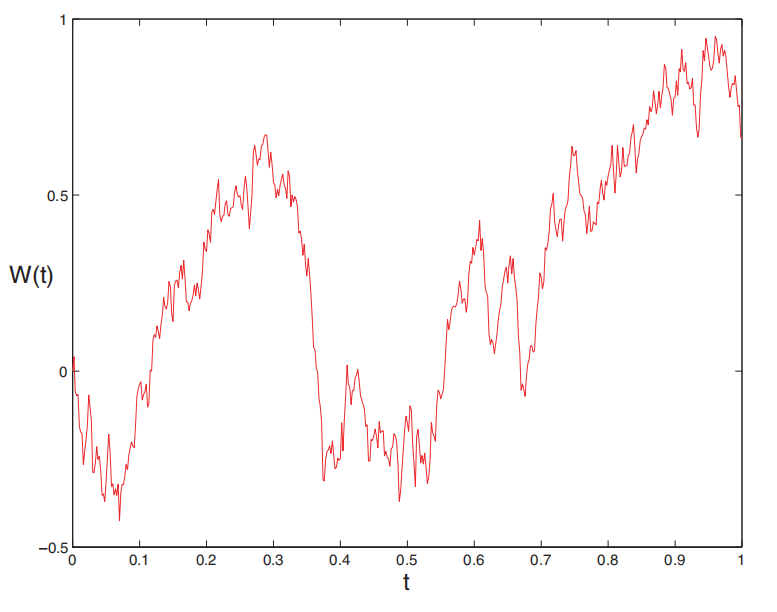
图:离散布朗路径

图:真解与电磁近似
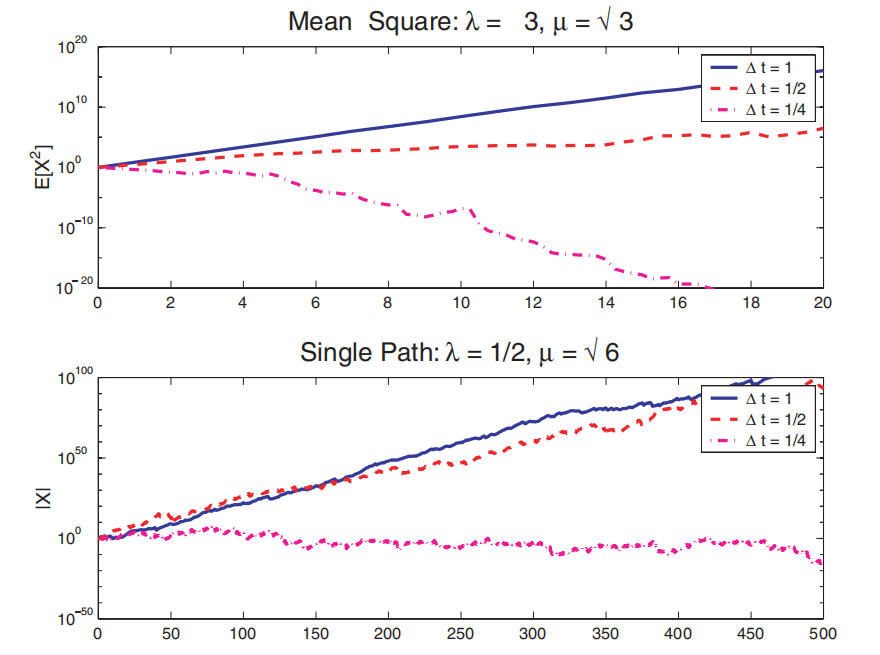
图:均方和渐近稳定性检验

图:均方和渐近稳定区域
文三:

大规模机器学习的优化方法
摘要:
本文对机器学习应用中的数字优化算法的过去、现在和未来进行了回顾和评论。通过文本分类和深度神经网络训练的案例研究,我们讨论了机器学习中如何出现操作优化问题,以及是什么使它们具有挑战性。我们研究的一个主要主题是,大规模机器学习代表了一种独特的环境,在这种环境中,随机梯度(SG)方法传统上发挥着核心作用,而传统的基于梯度的非线性优化技术通常会出现问题。基于这一观点,我们提出了一个简单但通用的SG算法的综合理论,讨论了它的实际行为,并强调了设计具有改进性能的算法的机会。这导致了对大规模机器学习的下一代优化方法的讨论,包括对减少随机方向噪声的技术和使用二阶导数近似的方法的两个主要研究流的调查。
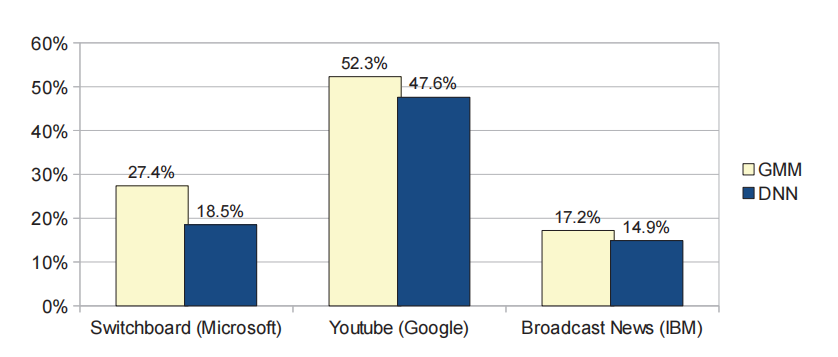
图:三个不同研究小组在三个标准语音识别基准上报告的单词错误率。

图:图像识别体系结构
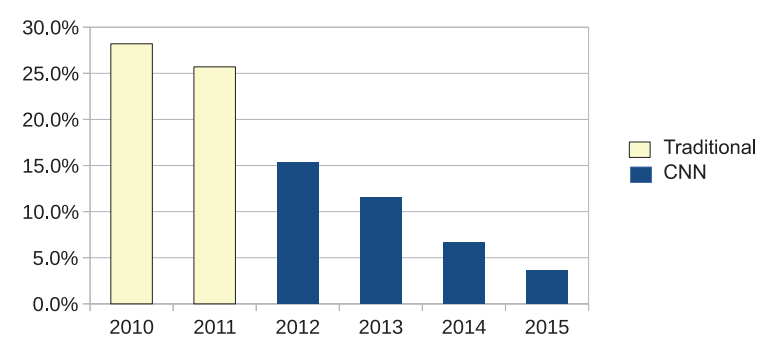
图:ImageNet图像分类挑战年度冠军的历史前5名错误率。卷积神经网络(CNN)在2012年实现了比所有传统方法的显著性能改进。接下来的几年巩固了细胞神经网络作为视觉对象识别领域的最新技术
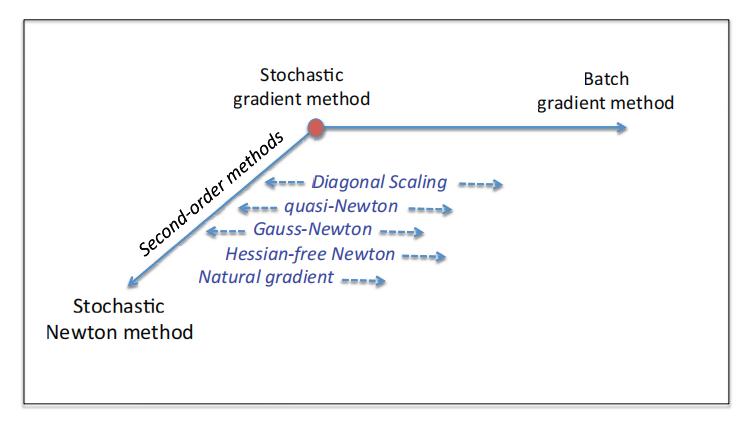
图:从图3.3看示意图,重点是二阶方法。
文四:

深度学习:应用数学家导论
摘要:
多层人工神经网络在许多应用领域正成为一种普及的工具。这场深度学习革命的核心是来自应用数学和计算数学的熟悉概念,尤其是微积分、近似理论、优化和线性代数。本文从应用数学的角度简要介绍了深度学习的基本思想。我们的目标受众包括渴望了解该领域的数学研究生和大四本科生。这篇文章也可能对那些希望通过参考深度学习技术的应用来活跃课堂的数学教师有用。我们关注三个基本问题:什么是深度神经网络?网络是如何训练的?什么是随机梯度法?我们用一个简短的MATLAB代码来说明这些想法,该代码用于建立和训练网络。我们还演示了在大规模图像分类问题上使用最先进的软件。我们最后参考了当前的文献。
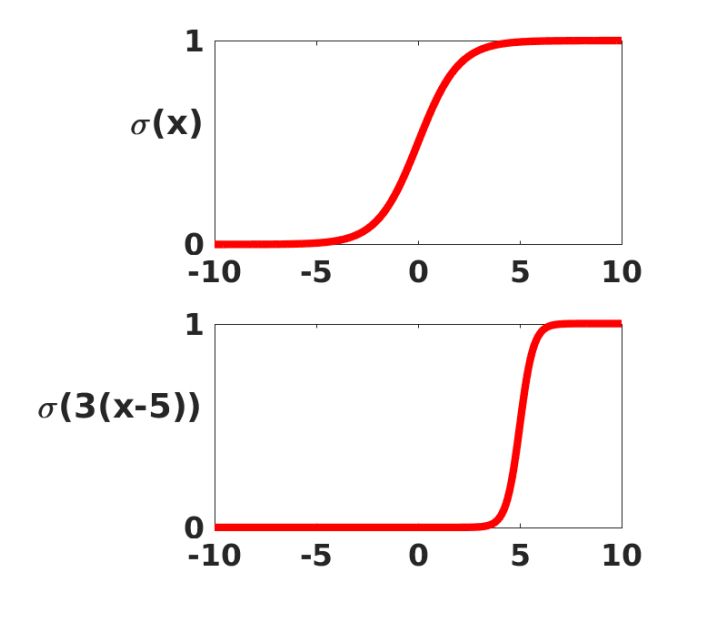
图:S形函数
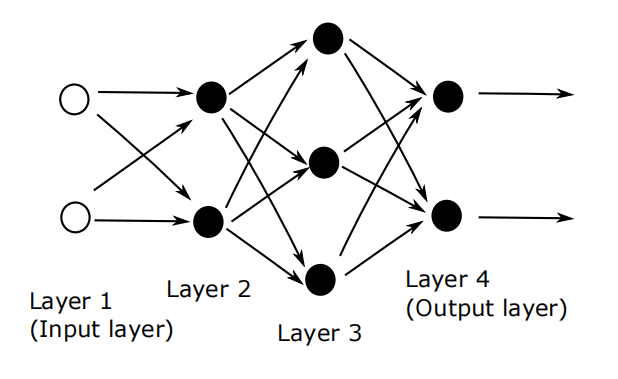
图:一个有四层的网络。

图:概述了 CNN 用于图像分类的任务

图:经过训练的网络错误分类的16张图像
文五:

了解图的嵌入方法及其应用
摘要:
图分析可以更好地定量理解和控制复杂网络,但传统方法存在计算成本高、内存要求过高等问题,这些问题与工业规模网络的高维性和异构性有关。图嵌入技术可以有效地将高维稀疏图转换为低维、密集、连续的向量空间,最大限度地保留图的结构性质。另一种新兴的图嵌入方法是使用基于正态分布的图嵌入来进行重要的不确定性估计。图嵌入方法的主要目标是将每个节点的属性集成到一个维数较小的向量中,从而可以利用标准度量方法在嵌入向量空间中量化原始复杂不规则空间中的节点相似性。在潜空间中生成的非线性、高度信息化的图形嵌入可以方便地用于处理不同的下游图形分析任务(如节点分类、链接预测、社区检测、可视化等)。本文介绍了图分析和图嵌入方法的一些基本概念,重点介绍了基于随机游动和基于神经网络的图嵌入方法。我们还讨论了新兴的基于深度学习的动态图嵌入方法。我们强调了图形嵌入方法在四种不同应用中的独特优势,并在补充材料中提供了实现细节和对开源软件以及可用数据库的参考,以帮助感兴趣的读者开始探索图形分析。
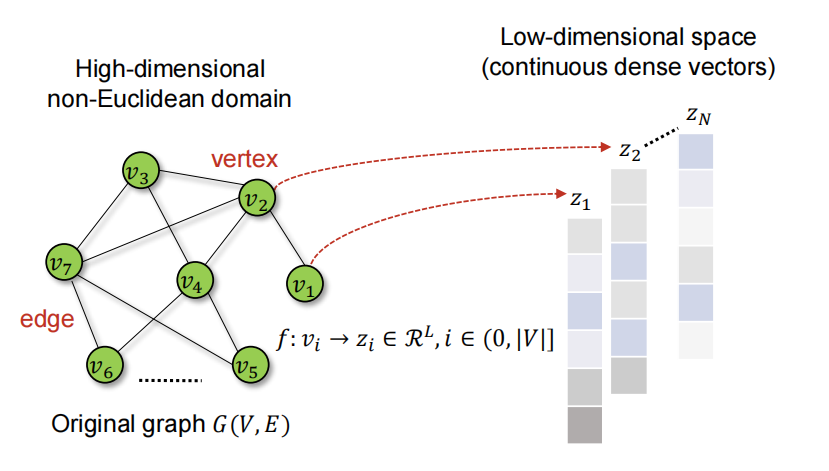
图:图(节点)嵌入示意图
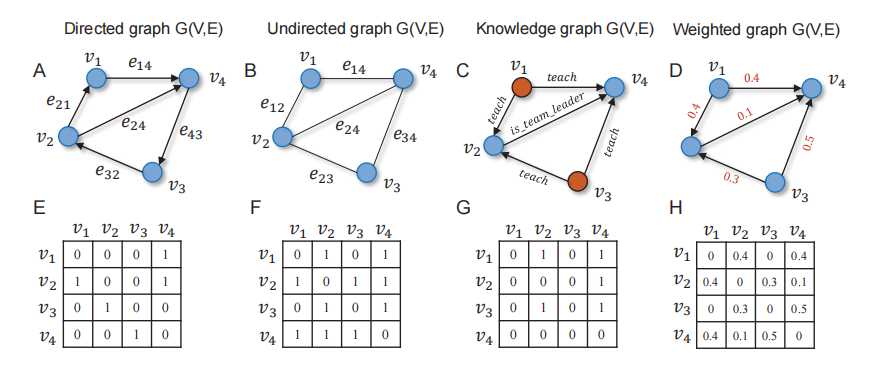
图:不同类型的图及其对应的邻接矩阵表示
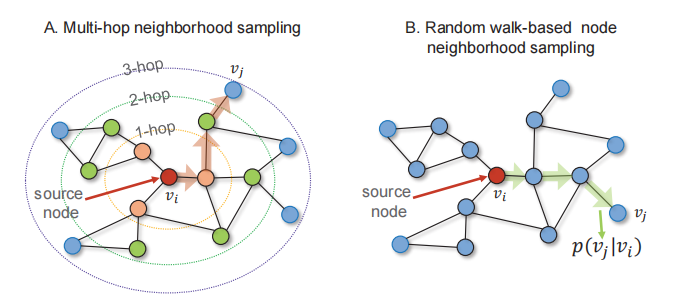
图:节点邻域采样技术。
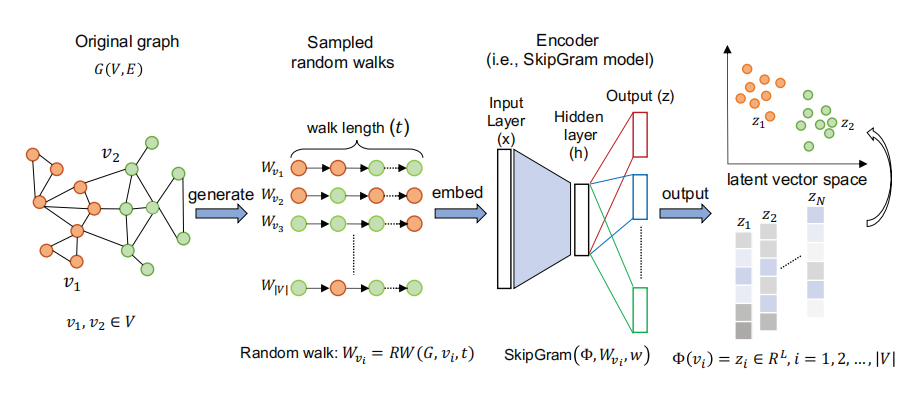
图:基于随机游动的流水线图嵌入方法




