AIforScience的交叉研究
文一:

人工智能时代的科学发现
摘要:
人工智能(AI)正越来越多地融入科学发现,以增强和加速研究,帮助科学家生成假设、设计实验、收集和解释大型数据集,并获得仅靠传统科学方法可能无法获得的见解。在这里,我们考察了过去十年的突破,包括自我监督学习,它允许在大量未标记的数据上训练模型,以及几何深度学习,它利用有关科学数据结构的知识来提高模型的准确性和效率。生成人工智能方法可以通过分析包括图像和序列在内的各种数据模式来创建设计,如小分子药物和蛋白质。我们讨论了这些方法如何在整个科学过程中帮助科学家,以及尽管取得了这些进步,但仍然存在的核心问题。人工智能工具的开发人员和用户都需要更好地了解这些方法何时需要改进,而糟糕的数据质量和管理带来的挑战仍然存在。这些问题跨越了科学学科,需要开发有助于科学理解或自主获取的基础算法方法,使其成为人工智能创新的关键关注领域。

图:人工智能时代的科学。科学发现是一个多方面的过程,涉及几个相互关联的阶段,包括假设形成、实验设计、数据收集和分析。人工智能准备通过在这一过程的每个阶段加强和加速研究来重塑科学发现。这里展示的原理和说明性研究突出了对增强科学理解和发现的贡献。

图:学习科学数据的有意义的表示

图:人工智能引导科学假设的产生。

图:人工智能与科学实验和模拟的集成。
文二:

应用统计物理学对抗人工智能增强分子动力学的陷阱
摘要:
基于人工智能的方法通过从原始数据中提取相关信息的能力,在整个科学领域产生了无可争辩的影响。最近,人工智能也被用于提高分子模拟的效率,其中人工智能衍生的慢模式被用于以有针对性的方式加速模拟。然而,尽管使用人工智能的典型领域的特点是数据过多,但分子模拟在每个结构中都受到有限的采样,因此数据有限。因此,在分子模拟中使用人工智能可能会遇到一种危险的情况,即人工智能优化可能会陷入虚假状态,导致手头问题的反应坐标(RC)的错误表征。当这样一个不正确的RC被用来进行额外的模拟时,人们可能会开始逐渐偏离基本事实。为了解决虚假人工智能解决方案的问题,我们报告了一种新颖的自动化算法,该算法使用了统计力学的思想。它基于这样一种理念,即更可靠的人工智能解决方案将是最大限度地实现慢过程和快过程之间的时间间隔。为了从有限的数据中学习这种时间尺度的分离,我们使用了一个基于最大口径的框架。我们展示了这种自动方案对三个经典基准问题的适用性,即模型肽的构象动力学、配体与蛋白质的脱键以及蛋白质G的C末端结构域的折叠/展开能量景观。我们相信,我们的工作将使可信赖的人工智能在复杂系统的分子模拟中得到更多和稳健的使用。

图:描述丙氨酸九肽构象动力学的RC的伪AI解。

图:流程图说明了我们筛选人工智能解决方案的新颖且计算高效的协议。从短期无偏MD模拟开始,我们的协议自动筛选在基于AI的方法中获得的虚假解,并学习最优RC。在这项工作中,我们证明了我们的协议在RAVE环境中的适用性,并且通过基于路径熵的过程来实现对虚假解决方案的筛选。

图:捕获丙氨酸二肽中的假AI溶液

图:从无偏MD中捕获GB1-C16的动力学
文三:

利用人工智能辅助分子动力学发现蛋白质构象的灵活性
摘要:
蛋白质对不同于其晶体结构的各种构象进行取样。这些结构、它们的倾向以及它们之间的移动路径包含了大量关于蛋白质功能的信息,这些信息从纯粹的结构角度来看是隐藏的。分子动力学模拟可以揭示这些替代构象,但通常需要高昂的计算成本。在这里,我们应用我们最近的统计力学和基于人工智能的分子动力学框架来增强蛋白质环的采样。我们通过对经典测试片蛋白T4溶菌酶的三个突变体的研究来举例说明这种方法。我们能够根据它们激发态的稳定性对它们进行正确的排序。通过分析反应坐标,我们还获得了至关重要的见解,了解为什么序列空间中的这些特定扰动会导致构象灵活性的巨大变化。因此,我们的框架允许在最小的先前人类偏差的情况下准确比较环构象群体,并应直接适用于生物学、化学及其他领域的一系列大分子。
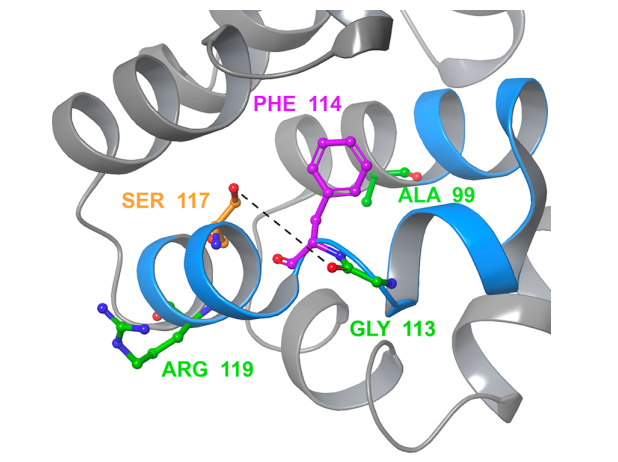
图:单突变体 L99A 的晶体结构与腔相邻环(残基100-120)显示为蓝色
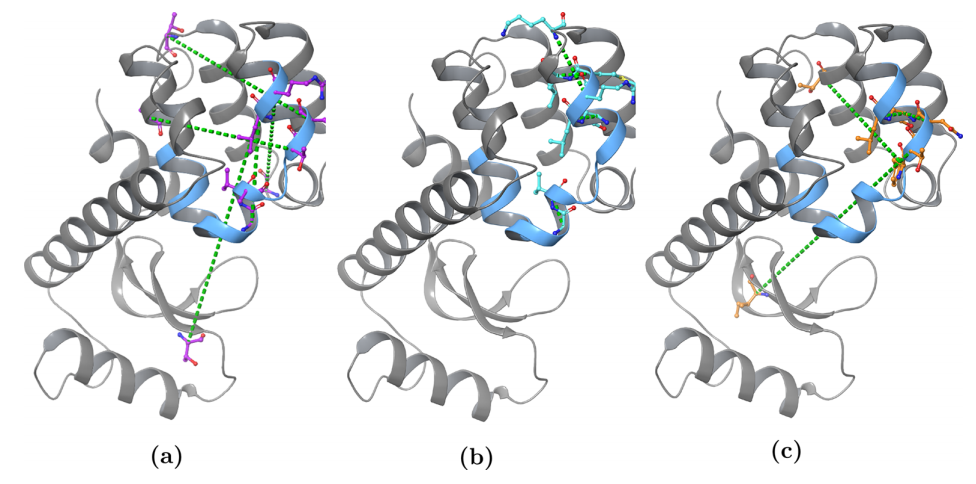
图:每个突变体的两个RC组分中的每个组分中三个最高加权OP的视觉表示。
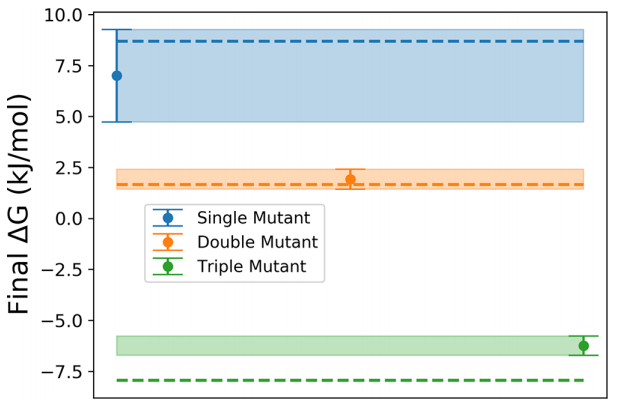
图:在500ns的元动力学模拟之后,使用每个状态的两个复 制品来确定激发态和基态之间的自由能差。
文四:

用于分析和增强分子动力学模拟的机器学习方法
摘要:
由于计算能力和软件可用性的提高,分子动力学(MD)已成为研究生物物理系统的强大工具。尽管MD为更好地理解这些复杂的生物物理系统做出了许多贡献,但仍有方法上的困难需要克服。首先,如何使运行中产生的大量数据,即使是一微秒长的MD模拟,也能让人理解。其次,如何有效地对下面的自由能表面和动力学进行采样。在这个简短的视角中,我们总结了基于机器学习的思想,这些思想解决了这两个局限性,重点是它们的关键理论基础和剩余的挑战。

图:示意图说明了使用机器学习来分析和增强MD模拟的一些方法的典型工作流程。描述系统在配置空间中的时间演化的高维数据被用作人工神经网络的输入。人工神经网络被训练以将输入投影到低维空间。根据神经网络和目标函数的结构,低维表示捕获了被认为是重要的不同特征,例如慢模式。在一些方法中,所学习的特征用于进一步增强MD模拟的采样,如底部箭头所示。
文五:

通过基于简化的对特异性从头算力场的分子动力学模拟,研究了由甲烷、二氧化碳和丙烷组成的二元流体混合物的菲克扩散系数
摘要:
为了用分子动力学(MD)模拟计算流体的热物理性质,经常使用针对实验汽液平衡进行优化的有效力场(FF)。该FF类别的示例有TraPPE、OPLS和AMBER。另一种选择是简化的基于从头算的配对特异性FF(AI FF),它是从零密度极限下的量子化学计算中结合气体动力学理论得出的,因此具有预测性。在本研究中,我们表明,在选定的二元流体混合物的帮助下,MD模拟在计算Fick扩散系数时的预测能力可以使用基于纯物质相应FF的简化对特异性AI FF来提高。为了评估新型AI FF与TraPPE FF的性能,研究了由甲烷、二氧化碳和丙烷组成的二元混合物,从过热蒸汽到气态,从超临界区域到压缩液态。为了确定在(0.1和12)MPa之间的压力、(293和355)K之间的温度以及0.05和0.95之间的摩尔分数下的Fick扩散系数,考虑到系统尺寸效应,对MaxwelleTefan扩散系数和热力学因子的分析进行了单独的模拟。除了压缩液体状态和两相边界附近的区域,其中TraPPE FF通常是优越的,AI FF显示出对Fick扩散系数的改进预测,平均扩展统计不确定性为12%。这可以通过将模拟结果与理论从头计算和可用的实验数据进行比较来证明,导致AI FF和TraPPE FF的平均绝对偏差分别为7%和13%。

图:KirkwoodeBuff系数Gij是由CH4(物种1)和CO2(物种2)组成的等摩尔二元混合物在295K和10MPa下R的倒数的函数,基于具有AI FF的20ns的模拟运行

图:不同对CH4eCH4(实线)、CO2eCO2(虚线)和CH4eCO2(点线)的集体 位移Dri$Drj的乘积(上部),以及由CH4和CO2组成的等摩尔二元混合物在295K和0.1MPa下的相应b系数(下部),通过使用我们的AI FF的1ms的五次独立MD模拟运行(彩色线)计算得出




