物质点法(Material Point Method)常见术语(一)
1. partial differential equations (PDE)
偏微分方程。
在数学中,偏微分方程(PDE)是一种计算多变量函数的各种偏导数之间的函数的方程。该函数通常被认为是一个需要求解的“未知量”的数学表达。然而,通常不可能写出偏微分方程解的显式公式。
偏微分方程在物理和工程等以数学为导向的科学领域普遍存在。例如,它们是现代科学对声音、热、扩散、静电、电动力学、热力学、流体动力学、弹性、广义相对论和量子力学(薛定谔方程、泡利方程等)理解的基础。它们也源于许多纯粹的数学考虑,如微分几何和变分法。
2. Boundary value problem(BVP)
边界值问题
在微分方程的研究中,边值问题是一个受到称为边界条件的约束的微分方程。边值问题的解是同样满足边界条件的微分方程的解。边值问题出现在物理学的几个分支中。在波动方程的问题,如法向模式的确定,通常被称为边值问题。一大类重要的边值问题是Sturm–Liouville问题。在线性情况下,对这些问题的分析涉及微分算子的本征函数。
为了在应用中有用,边值问题应该是适定的。这意味着,给定问题的输入,就存在一个唯一的解决方案,该解决方案持续依赖于输入。偏微分方程领域的许多理论工作都致力于证明科学和工程应用中产生的边值问题实际上是适定的。最早研究的边值问题是狄利克雷问题,即求调和函数(拉普拉斯方程的解);解是由狄利克雷原理给出的。
3. Initial value problem(IVP)
初始值问题
初始值问题是一个常微分方程和一个初始条件,该初始条件指定了域中给定点上未知函数的值。在物理学或其他科学中对系统进行建模通常相当于解决初始值问题。在这种情况下,微分初值是一个方程,它规定了在给定问题初始条件的情况下,系统如何随时间演化。
4. Finite element method(FEM)
有限单元法
有限元法(FEM)是工程和数学建模中常用的数值求解微分方程的方法。适用的典型问题领域包括结构分析、传热、流体流动、传质和电磁势等传统领域。有限元法是求解两个或三个空间变量中的偏微分方程(即一些边值问题)的通用数值方法。为了解决问题,有限元法将一个大系统细分为更小、更简单的部分,称为有限元。这是通过空间维度中的特定空间离散化来实现的,该离散化通过构建对象的网格来实现:解的数值域,其具有有限数量的点。边值问题的有限元法公式最终得到一个代数方程组。该方法近似域上的未知函数。然后,对这些有限元进行建模的简单方程组被组装成一个更大的方程组,对整个问题进行建模。然后,FEM通过变分法最小化相关的误差函数来近似求解。
5. Finite volume method(FVM)
有限体积法
有限体积法(FVM)是以代数方程的形式表示和求解偏微分方程的一种方法。在有限体积法中,包含发散项的偏微分方程的体积积分通过高斯散度定理转化为表面积分。然后将这些项作为每个有限体积表面的通量进行计算。因为进入给定体积的通量与离开相邻体积的通量相同,所以这些方法是保守的。有限体积法的另一个优点是,它很容易公式化,以考虑非结构化网格。这种方法在许多计算流体力学软件包中都有使用。“有限体积”是指网格上每个节点周围的小体积。有限体积方法可以与差分方法进行比较和对比,后者使用节点值逼近导数,或者有限元方法使用局部数据创建解的局部近似,并通过将它们拼接在一起构造一个全局近似。相比之下,有限体积法计算某个体积上解的平均值的精确表达式,并使用这些数据在单元格内构造解的近似值。
6. Finite difference method(FDM)
有限差分法
在数值分析中,有限差分法(FDM)是一种通过逼近有限差分导数来求解微分方程的数值技术。空间域和时间间隔(如果适用)都是离散化的,或者分成有限个步骤,并且通过求解包含有有限差分和附近点的值的代数方程来近似这些离散点上的解的值。差分方法把非线性的常微分方程(ODE)或偏微分方程(PDE)转换成可以用矩阵代数技术求解的线性方程组。现代计算机能够有效地执行这些线性代数计算,加上它们相对容易的实现,使得有限差分法在现代数值分析中得到了广泛的应用。时域有限差分法和有限元法是目前求解偏微分方程数值解最常用的方法之一。
7. Meshless or Meshfree methods(MMs)
无网格化方法
在数值分析领域,无网格方法是那些不需要模拟域的节点之间的连接,即一个网格,而是基于每个节点与其所有邻居的相互作用的方法。因此,原来的广泛性质,如质量或动能,不再分配给网格单元,而是单一的节点。无网格方法能够模拟一些其他困难类型的问题,代价是额外的计算时间和编程工作。没有网格允许拉格朗日模拟,其中节点可以根据速度场移动。
有限差分法、有限体积法和有限元法等数值方法最初是在数据点的网格上定义的。在这样的网格中,每个点都有固定数量的预定义邻居,并且邻居之间的这种连通性可以用于定义数学运算符,如导数。然后,这些运算符用于构建要模拟的方程,例如欧拉方程或纳维-斯托克斯方程。但是,在模拟中,被模拟的材料可以四处移动(如在计算流体动力学中),或者在材料可能发生大变形的情况下(如在塑料材料的模拟中),网格的连通性可能很难保持,而不会在模拟中引入误差。如果网格在模拟过程中变得缠结或退化,则在其上定义的操作符可能不再提供正确的值。网格可以在模拟过程中重新创建(一个称为重新网格的过程),但这也可能会引入错误,因为所有现有的数据点都必须映射到一组新的不同数据点上。无网格方法旨在解决这些问题。无网格方法也适用于:
根据复杂三维对象的几何图形创建有用网格可能特别困难或需要人工协助的模拟
可能创建或销毁节点的模拟,例如在开裂模拟中
问题几何体可能与固定网格不对齐的模拟,例如在弯曲模拟中
包含非线性材料行为、不连续性或奇点的模拟
8. Discrete Time
离散时间
离散时间将变量的值视为发生在不同的、独立的“时间点”,或者相当于在每个非零的时间区域(“时间周期”)中没有变化ーー也就是说,时间被视为一个离散变量。因此,当时间从一个时间周期移动到下一个时间周期时,一个非时间变量从一个值跳跃到另一个值。
这种时间观相当于一个数字时钟,在一段时间内给出10:37的固定读数,然后跳转到新的10:38的固定读数,等等。在这个框架中,每个感兴趣的变量在每个时间段测量一次。任意两个时间周期之间的测量次数是有限的。测量通常以变量“时间”的连续整数值进行。离散信号或离散时间信号是由一系列量组成的时间序列。
与连续时间信号不同,离散时间信号不是连续参数的函数; 然而,它可能是通过从连续时间信号采样获得的。当一个离散时间信号通过在均匀间隔时间内对一个序列进行采样获得时,它具有一个相关的采样率。离散时间信号可能有几个来源,但通常可以分为两组之一: 通过以恒定或可变速率获取模拟信号的值。这个过程称为采样通过观察一个固有的离散时间过程,例如一个特定经济指标的周峰值。
9. Continuous Time
连续时间
相反,连续时间将变量视为仅在极短的时间内具有特定值。在任何两个时间点之间都有无限多的其他时间点。变量“时间”的范围在整个实数线上,或者根据上下文,在它的某个子集上,如非负实数。因此,时间被视为一个连续的变量。
连续信号或连续时间信号是一个变化量(信号),其域(通常是时间)是一个连续体(例如,实数的连通区间)。也就是说,函数的域是一个不可数集。函数本身不需要是连续的。相反,离散时间信号有一个可数域,就像自然数一样。
具有连续幅度和时间的信号被称为连续时间信号或模拟信号。这个(信号)在每一个时刻都有一定的价值。与温度、压力、声音等物理量成比例导出的电信号通常是连续信号。连续信号的其他例子是正弦波、余弦波、三角波等。
信号是在域上定义的,域可以是有限的,也可以不是有限的,并且存在从域到信号值的函数映射。时间变量的连续性,结合实数密度定律,意味着信号值可以在任意时间点找到。
10. Euler method
欧拉方法
在数学和计算科学中,欧拉方法(也称为正向欧拉方法)是求解具有给定初始值的常微分方程(ODEs)的一阶数值过程。它是常微分方程数值积分最基本的显式方法,也是最简单的龙格-库塔方法。
欧拉方法是一阶方法,这意味着局部误差(每一步的误差)与步长的平方成正比,全局误差(给定时间的误差)则与步长成正比。欧拉方法通常作为构建更复杂方法的基础,例如预测-校正方法。
11. Backward Euler method
后向欧拉方法
在数值分析和科学计算中,后向欧拉法(或隐式欧拉法)是求解常微分方程的最基本的数值方法之一。它类似于(标准)Euler方法,但不同之处在于它是一种隐式方法。后向欧拉方法在时间上有一阶误差。
12. Explicit and implicit methods
显式方法和隐式方法
显式和隐式方法是数值分析中使用的方法,用于获得含时常微分方程和偏微分方程解的数值近似值,这是物理过程计算机模拟所要求的。显式方法根据系统在当前时间的状态计算系统在以后时间的状态,而隐式方法通过求解涉及系统当前状态和以后状态的方程来找到解决方案。
对于显式方法有:
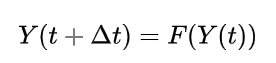
对于隐式方法有:
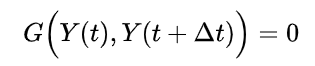
13. Runge-Kutta method
龙格卡库方法
在数值分析中,龙格-库塔方法是一类隐式和显式迭代方法,其中包括欧拉方法,用于非线性联立方程近似解的时间离散化。这些方法是由德国数学家卡尔·伦格和威廉·库塔在1900年左右发展起来的。
14. Galerkin method
伽辽金方法
在数学中,在数值分析领域,伽辽金方法是以苏联数学家鲍里斯·伽辽金的名字命名的。它们通过应用由有限组基函数确定的线性约束,将连续算子问题(如微分方程)转化为离散问题,通常采用弱公式。
15. Strong Form & Weak Form
强形式与弱形式
何为强形式与弱形式?其区分在于是否完全满足物理模型的条件所谓强形式,满足物理模型的条件,进行偏微分控制方程求解。也就是需要满足的条件太复杂。比如不连续点的跳跃等等。这就会导致极难找到满足偏微分方程强形式的解析解的。而将微分方程转化为弱形式就是弱化对方程解的要求不拘泥于个别特殊点的要求,而放松为一段有限段上需要满足的条件,使解能够以离散的形式存在。
16. ordinary differential equations (ODEs).
常微分方程
在数学中,常微分方程是一个只依赖于一个独立变量的微分方程。与其他 DE 一样,它的未知函数由一个(或多个)函数组成,并涉及这些函数的导数。“普通”一词与偏微分方程形成对比,偏微分方程可能涉及一个以上的自变量。
17. Navier-Stokes (N-S) Equation
纳维尔斯托克斯方程
Navier-Stokes 方程是描述粘性流体物质运动的偏微分方程。它们以法国工程师和物理学家克劳德-路易·纳维以及爱尔兰物理学家和数学家乔治·加布里埃尔·斯托克斯的名字命名。从1822年(纳维尔)到1842-1850年(斯托克斯) ,经过几十年逐步建立这些理论,它们得到了发展。
Navier-Stokes 方程数学表达了牛顿流体的动量平衡和质量守恒。它们有时伴随着一个与压力、温度和密度相关的状态方程。它们产生于将牛顿第二定律应用于流体运动,以及流体中的应力是扩散粘性项(与速度梯度成正比)和压力项之和的假设,因此描述了粘性流动。它们与密切相关的欧拉方程的区别在于,纳维尔-斯托克斯方程考虑了粘性,而欧拉方程只考虑了无粘流动。因此,Navier-Stokes 方程是一个抛物型方程,因此具有更好的解析性质,代价是数学结构较少(例如,它们从来不是完全可积的)。
纳维尔-斯托克斯方程是有用的,因为它们描述了许多科学和工程感兴趣的现象的物理学。它们可以用来模拟天气、洋流、管道中的水流和机翼周围的空气流动。纳维尔-斯托克斯方程的完整和简化形式有助于飞机和汽车的设计、血液流动的研究、电站的设计、污染分析以及许多其他问题。结合麦克斯韦方程组,它们可以用来建模和研究磁流体力学。
纳维尔-斯托克斯方程在纯数学意义上也很有趣。尽管它们有着广泛的实际用途,但是还没有证明光滑解是否总是存在于三维空间中ーー也就是说,它们是否在领域的所有点上都是无穷可微的(甚至仅仅是有界的)。这就是 Navier-Stokes 存在性和光滑性问题。克雷数学研究所称这是数学中七个最重要的公开问题之一,并为一个解决方案或反例提供了100万美元的奖金。
18. Smoothed Particle Hydrodynamics (SPH)
光滑粒子流体动力学
光滑粒子流体力学(SPH)是一种用于模拟连续介质力学的计算方法,如固体力学和流体流动。它是由Gingold、Monaghan和Lucy于1977年开发的,最初是为了解决天体物理问题。它已被用于许多研究领域,包括天体物理学、弹道学、火山学和海洋学。这是一种无网格拉格朗日方法(坐标随流体移动),该方法的分辨率可以很容易地根据密度等变量进行调整。
优势
通过构造,SPH 是一种无网格方法,这使得它非常适合于模拟由复杂的边界动力学支配的问题,如自由表面流动或大的边界位移。
缺少网格极大地简化了模型的实现及其并行化,即使对于多核架构也是如此。
正如建模物理学中所讨论的那样,SPH 可以很容易地扩展到各种各样的领域,并且可以与其他一些模型杂交。
正如在弱可压缩 SPH 一节中所讨论的,该方法具有很大的守恒特性。
当感兴趣的度量与流体密度(例如密度波动的概率密度函数)相关时,每个粒子数的 SPH 模拟的计算成本显著低于每个单元数的网格模拟成本。之所以是这样,是因为在 SPH 中,解决方案被放在问题所在的位置。
局限性
在 SPH 中设置边界条件,如入口和出口和墙壁比基于网格的方法更困难。事实上,有人说“边界条件的处理肯定是 SPH 方法最困难的技术问题之一”。这个挑战部分是因为在 SPH 中,边界附近的粒子随时间而变化。尽管如此,SPH 的壁边界条件是可用的。
当感兴趣的度量与密度(例如动能谱)不(直接)相关时,每个粒子数量的 SPH 模拟的计算成本显着大于每个细胞数量的基于网格的模拟成本。因此,忽略并行加速比的问题,用基于网格的方法模拟等密度流动(例如,外部空气动力学)比用 SPH 更有效。
19. Interpolation
插值
在数值分析的数学领域中,插值是一种估计,是一种基于已知数据点的离散集的范围构建(找到)新数据点的方法。
在工程和科学中,通常有许多通过采样或实验获得的数据点,这些数据点表示自变量的有限值的函数值。通常需要进行插值;即,估计自变量的中间值的该函数的值。
一个密切相关的问题是用简单函数逼近复杂函数。假设某个给定函数的公式是已知的,但过于复杂,无法有效地进行评估。可以对原始函数中的一些数据点进行插值,以生成一个更简单的函数,该函数仍然相当接近原始函数。由此产生的简单增益可以超过插值误差的损失,并在计算过程中提供更好的性能。
20. Numerical intergration
数值积分
在分析中,数值积分包括一系列计算定积分数值的算法。




